Chapter 5 maths class 9 exercise 5.1 || class 9 maths exercise 5.1 || introduction to euclid's geometry class 9 || class 9 maths exercise 5.1 solution || exercise 5.1 class 9 maths || class 9 maths chapter 5 exercise 5.1 solutions || ncert class 9 exercise 5.1
Explore clear, step-by-step solutions for Class 9 Maths Chapter 5, Exercise 5.1, based on Euclid’s Geometry. This exercise introduces students to the foundational principles of geometry through Euclid’s definitions, axioms, and postulates. By working through these problems, learners develop a logical and structured approach to geometric reasoning. Exercise 5.1 helps students understand how all geometric concepts are built from simple, well-defined terms and assumptions. Engaging with this exercise strengthens their ability to form logical arguments, distinguish between axioms and theorems, and appreciate the systematic nature of mathematical thought—laying the groundwork for more advanced geometry in higher classes.

chapter 5 maths class 9 exercise 5.1 || class 9 maths exercise 5.1 || introduction to euclid's geometry class 9 || class 9 maths exercise 5.1 solution || exercise 5.1 class 9 maths || class 9 maths chapter 5 exercise 5.1 solutions || ncert class 9 exercise 5.1
Exercise 5.1
1. Which of the following statements are true and which are false? Give reasons for your answers.
Since, there can be infinite lines that can be drawn passing through a single point.
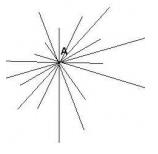
As in the diagram from point A, infinitely many lines can be drawn.
Only and only one line can be drawn which passes through two distinct points.

As you can see only one line can be drawn through two points.
A terminated line can be produced indefinitely on both the sides. A line can be extended in both directions. A line refers to infinite long length
If two circles are equal, then their radii are equal.
By superposition, we will find that the center and circumference of the both circles coincide. Hence, their radius ought to be equal.
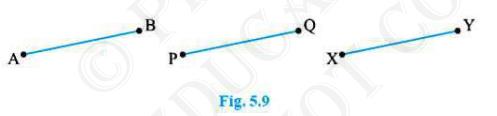
By Euclid's first axiom things which are equal to the same thing, are equal to one another.
chapter 5 maths class 9 exercise 5.1 || class 9 maths exercise 5.1 || introduction to euclid's geometry class 9 || class 9 maths exercise 5.1 solution || exercise 5.1 class 9 maths || class 9 maths chapter 5 exercise 5.1 solutions || ncert class 9 exercise 5.1
2. Give a definition for each of the following terms. Are there other terms that need to be defined first? What are they, and how might you define them?
Plane: A plane is a flat surface on which geometric figures are drawn.
Point: A point is a dimensionless dot which is drawn on a plane surface.
Line: A line is collection of n number of points which can extend in both the directions and has only one dimension.
Now,
Parallel lines: When two or more lines do not intersect each other in a plane and perpendicular distance between them remains constant then they are said to be parallel lines.
Plane: A plane is a flat surface on which geometric figures are drawn.
Point: A point is a dimensionless dot which is drawn on a plane surface.
Line: A line is collection of n number of points which can extend in both the directions and has only one dimension.
Now,
Perpendicular lines: When two lines intersect each other making a right angle in a plane then they are said to be perpendicular to each other.
Plane: A plane is a flat surface on which geometric figures are drawn.
Point: A point is a dimensionless dot which is drawn on a plane surface.
Line: A line is collection of n number of points which can extend in both the directions and has only one dimension.
Now,
Line segment: A line segment is a part of a line with two end points and cannot be extended further. It has a definite length or breadth.
chapter 5 maths class 9 exercise 5.1 || class 9 maths exercise 5.1 || introduction to euclid's geometry class 9 || class 9 maths exercise 5.1 solution || exercise 5.1 class 9 maths || class 9 maths chapter 5 exercise 5.1 solutions || ncert class 9 exercise 5.1
Plane: A plane is a flat surface on which geometric figures are drawn.
Point: A point is a dimensionless dot which is drawn on a plane surface.
Line: A line is collection of n number of points which can extend in both the directions and has only one dimension.
Now,
Radius of circle: The fixed distance between the centre and the circumference of the circle is called radius of the circle.
Plane: A plane is a flat surface on which geometric figures are drawn.
Point: A point is a dimensionless dot which is drawn on a plane surface.
Line: A line is collection of n number of points which can extend in both the directions and has only one dimension.
Now,
Square: A square is a quadrilateral in which all the four sides are equal and each internal angle is a right angle.
(i) Given any two distinct points A and B, there exists a third point C which is in between A and B.
(ii) There exist at least three points that are not on the same line.
Do these postulates contain any undefined terms? Are these postulates consistent?
Do they follow from Euclid's postulates? Explain.
\(\bullet\) Here, there is no information given about the plane whether the points are in same plane or not.
\(\bullet\) Also, n number of points lie in a plane. But here the position of the point C is not specified that whether it lies on the line segment joining AB or not.
Yes, these postulates are consistent when we deal with these two situations:
(i) Point C is lying in between and on the line segment joining A and B.

(ii) Point C not lies on the line segment joining A and B.

No, they don't follow from Euclid's postulates. They follow the axioms.
\(\mathrm{AC}=\mathrm{BC}\)

Now,
After adding \(\mathrm{AC}\) both side, we get
\(\mathrm{AC}+\mathrm{AC}=\mathrm{BC}+\mathrm{AC}\)
\( 2 \mathrm{AC}=\mathrm{AB} \) (Since, If equals are added to equals, the wholes are equal.)
Therefore,
\(\mathrm{AC}=\frac{1}{2} \mathrm{AB}\)
Let A and B be the line segment and points P and Q be two different midpoints of AB .
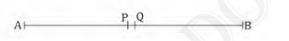
So,
\(\mathrm{AP}=\mathrm{PB}\)
And,
\(\mathrm{AQ}=\mathrm{QB}\)
And,
\( \mathrm{PB}+\mathrm{AP}=\mathrm{AB} \) (It coincides with line segment AB\( ) \)
Similarly,
\(\mathrm{QB}+\mathrm{AQ}=\mathrm{AB}\)
Now,
\( \mathrm{AP}+\mathrm{AP}=\mathrm{AP}+\mathrm{BP} \) (Since, If equals are added to equals, the wholes are equal.)
\(2 \mathrm{AP}=\mathrm{AB}\quad \ldots\ldots\text{(i)}\)
Similarly,
\(2 \mathrm{AQ}=\mathrm{AB}\quad \ldots\ldots\text{(ii)}\)
From (i) and (ii),
\( 2 \mathrm{AP}=2 \mathrm{AQ} \) (Since things which are equal to the same thing are equal to one another)
And as we know:
Things which are double of the same thing are equal to one another.
Therefore,
\(\mathrm{AP}=\mathrm{AQ}\)
Thus, P and Q are the same points.
This contradicts the fact that P and Q are two different midpoints AB.
Thus, it is proved that every line segment has one and only one midpoint.
Method 2:

From the Figure, \( \mathrm{AP}+\mathrm{PB}=\mathrm{AB} \quad \ldots\ldots\text{(i)}\)
\( \mathrm{AQ}+\mathrm{QB}=\mathrm{AB} \quad \ldots\ldots\text{(ii)}\)
From eq(i) and eq(ii)
\( \mathrm{AP}+\mathrm{PB}=\mathrm{AQ}+\mathrm{QB} \) Now let \( \mathrm{AP}=\mathrm{PB} \), and \( \mathrm{AQ}=\mathrm{QB} \) (as they are the midpoints, then)
\( 2 \mathrm{AP}=2 \mathrm{AQAP}=\mathrm{AQP}=\mathrm{Q} \) Hence, there is only one midpoint.
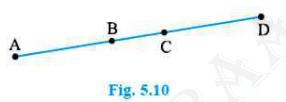
From the figure,
\(\mathrm{AC}=\mathrm{AB}+\mathrm{BC}\)
\(\mathrm{BD}=\mathrm{BC}+\mathrm{CD}\)
\(\mathrm{AB}+\mathrm{BC}=\mathrm{BC}+\mathrm{CD}\)
According to Euclid's axiom,
When two equals are subtracted from equals, remainders are also equal.
Subtracting BC both sides,
\(\mathrm{AB}+\mathrm{BC}-\mathrm{BC}=\mathrm{BC}+\mathrm{CD}-\mathrm{BC}\)
\(\mathrm{AB}=\mathrm{CD}\)
Let us take an example of the cake. When it is whole it will measure 3 pound but when we took out a part from it and measure its weight then it would come out less than the previous one. Hence, the fifth axiom of Euclid is true for all the universal things. That is the reason that it is considered as a 'universal truth'.

