Class 9 maths chapter 5 exercise 5.2 solutions || ncert class 9 exercise 5.2 || chapter 5 maths class 9 exercise 5.2 || exercise 5.2 class 9 maths || class 9 maths exercise 5.2 solution || introduction to euclid's geometry class 9 || class 9 maths exercise 5.2
Explore clear, step-by-step solutions for Class 9 Maths Chapter 5, Exercise 5.2, centered on Euclid’s Geometry. This exercise extends students’ understanding of Euclid’s postulates by applying them to basic geometric situations. Through logical analysis and application of these postulates, learners enhance their deductive reasoning skills. Exercise 5.2 encourages students to examine how simple assumptions can lead to meaningful geometric results. By engaging with these problems, students learn to distinguish between definitions, axioms and postulates, and to apply them effectively in proofs—building a strong conceptual foundation for higher-level geometry.

class 9 maths chapter 5 exercise 5.2 solutions || ncert class 9 exercise 5.2 || chapter 5 maths class 9 exercise 5.2 || exercise 5.2 class 9 maths || class 9 maths exercise 5.2 solution || introduction to euclid's geometry class 9 || class 9 maths exercise 5.2
Exercise 5.2
1. How would you rewrite Euclid's fifth postulate so that it
would be easier to understand?
Answer
Euclid's Fifth Postulate: If a straight line falling on two
straight lines makes the interior angles on the same side of it
taken together less than two right angles, then the two straight
lines, if produced indefinitely, meet on that side on which the
sum of angles is less than two right angles.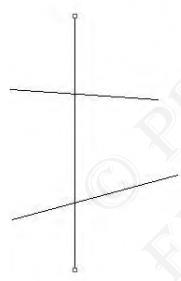
From the figure, we can see that the two lines that are not parallel and make acute angles, will intersect at the side which is towards the acute angle. Now we can look at this Postulate from a different point of view, we can say that the lines that are not parallel to each other, intersect with each other where the inclination is towards meeting them.
class 9 maths chapter 5 exercise 5.2 solutions || ncert class 9 exercise 5.2 || chapter 5 maths class 9 exercise 5.2 || exercise 5.2 class 9 maths || class 9 maths exercise 5.2 solution || introduction to euclid's geometry class 9 || class 9 maths exercise 5.2
2. Does Euclid's fifth postulate imply the existence of parallel
lines? Explain.
Answer
Fifth postulate of Euclid geometry: If a straight line falling on
two straight lines makes the interior angles on the same side of
it taken together less than two right angles, then the two
straight lines, if produced indefinitely, meet on that side on
which the sum of angles is less than two right angles.Now according to this postulate if the straight lines will not meet when the angles made are equal, the lines will not intersect and hence the lines are parallel.
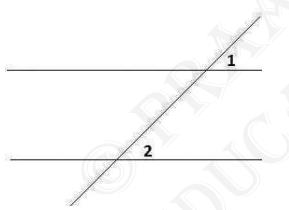
From the figure if angles 1 and 2 are equal then the lines when extended to infinity will not intersect and hence will be parallel.

