Ncert class 9 exercise 7.3 || exercise 7.3 maths class 9 || rd sharma class 9 triangle || chapter 7 maths class 9 exercise 7.3 || maths chapter 7 class 9 exercise 7.3 || class 9 maths chapter 7 exercise 7.3 solutions || class 9 ncert exercise 7.3 || exercise 7.3 class 9 maths || chapter 7 exercise 7.3 class 9
Explore clear, step-by-step solutions for Class 9 Maths Chapter 7, Exercise 7.3, which focuses on the congruence of right-angled triangles using the RHS (Right angle-Hypotenuse-Side) criterion. This exercise guides students in identifying when two right-angled triangles are congruent by comparing the hypotenuse and one side, along with the right angle. Through practical problems, learners enhance their understanding of triangle congruence in special cases and apply logical reasoning to prove geometrical facts. By practicing Exercise 7.3, students reinforce their proof-writing abilities and develop a strong base for higher-level geometric applications involving right-angled triangles, trigonometry, and constructions.

ncert class 9 exercise 7.3 || exercise 7.3 maths class 9 || rd sharma class 9 triangle || chapter 7 maths class 9 exercise 7.3 || maths chapter 7 class 9 exercise 7.3 || class 9 maths chapter 7 exercise 7.3 solutions || class 9 ncert exercise 7.3 || exercise 7.3 class 9 maths || chapter 7 exercise 7.3 class 9
Exercise 7.3
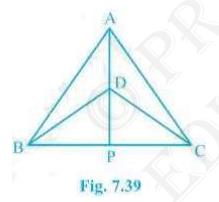
1. \( \triangle \mathrm{ABC} \) and \( \triangle \mathrm{DBC} \)
are two isosceles triangles on the same base \(BC\) and vertices
\( A \) and \( D \) are on the same side of \(BC\) (see Fig.
7.39). If \(AD\) is extended to intersect \( B C \) at \( P \),
show that
(i) \( \triangle \mathrm{ABD} \triangle \mathrm{ACD} \)
(ii) \( \triangle \mathrm{ABP} \triangle \mathrm{ACP} \)
(iii) \(AP\) bisects \(A\) as well as \(D\) .
(iv) \(AP\) is the perpendicular bisector of \(BC\) .
(i) \( \triangle \mathrm{ABD} \triangle \mathrm{ACD} \)
(ii) \( \triangle \mathrm{ABP} \triangle \mathrm{ACP} \)
(iii) \(AP\) bisects \(A\) as well as \(D\) .
(iv) \(AP\) is the perpendicular bisector of \(BC\) .

Answer
In the above question, it is given that \( \triangle \mathrm{ABC}
\) and \( \triangle \mathrm{DBC} \) are two isosceles
triangles.(i) \( \triangle \mathrm{ABD} \) and \( \triangle \mathrm{ACD} \) are similar by SSS congruency because:
\( \mathrm{AD}=\mathrm{AD} \) (It is the common arm)
\( \mathrm{AB}=\mathrm{AC} \quad( \) Since \( \triangle \mathrm{ABC} \) is isosceles)
\( \mathrm{BD}=\mathrm{CD} \) (Since \( \triangle \mathrm{DBC} \) is isosceles)
\( \therefore \triangle \mathrm{ABD} \triangle \mathrm{ACD} \).
(ii) \( \triangle \mathrm{ABP} \) and \( \triangle \mathrm{ACP} \) are similar as:
\(\mathrm{AP} =\mathrm{AP}\quad\) (It is the common side)
\(\mathrm{PAB} =\mathrm{PAC} (\text { by CPCT since } \triangle \mathrm{ABD} \Delta \mathrm{ACD})\)
\(\mathrm{AB} =\mathrm{AC} (\text { Since } \triangle \mathrm{ABC} \text { is isosceles })\)
So, \( \triangle \mathrm{ABP} \triangle \mathrm{ACP} \) by SAS congruency condition.
(iii) \( \mathrm{PAB}=\mathrm{PAC} \) by CPCT as \( \triangle \mathrm{ABD} \triangle \mathrm{ACD} \).
AP bisects A.
Also, \( \triangle \mathrm{BPD} \) and \( \triangle \mathrm{CPD} \) are similar by SSS congruency as \( \mathrm{PD}=\mathrm{PD} \quad \) (It is the common side)
\( \mathrm{BD}=\mathrm{CD} \) (Since \( \triangle \mathrm{DBC} \) is isosceles.)
\( \mathrm{BP}=\mathrm{CP} \quad( \) by CPCT as \( \triangle \mathrm{ABP} \triangle \mathrm{ACP}) \)
So, \( \triangle \mathrm{BPD} \triangle \mathrm{CPD} \).
Thus, \( \mathrm{BDP}=\mathrm{CDP}\) by CPCT.\(\ldots\)(ii)
Now by comparing (i) and (ii) it can be said that AP bisects A as well as D.
(iv) \( \mathrm{BPD}=\mathrm{CPD} \) (by CPCT as \( \triangle \mathrm{BPD} \triangle \mathrm{CPD} \) )
and \( \mathrm{BP}=\mathrm{CP} \ldots\)(ii)
also,
\( \mathrm{BPD}+\mathrm{CPD}=180^{\circ} \quad( \) Since BC is a straight line. \( ) \)
\( \Rightarrow 2 \mathrm{BPD}=180^{\circ} \)
\( \Rightarrow \mathrm{BPD}=90^{\circ} \)
Now, from equations (i) and (ii), it can be said that
AP is the perpendicular bisector of BC .
ncert class 9 exercise 7.3 || exercise 7.3 maths class 9 || rd sharma class 9 triangle || chapter 7 maths class 9 exercise 7.3 || maths chapter 7 class 9 exercise 7.3 || class 9 maths chapter 7 exercise 7.3 solutions || class 9 ncert exercise 7.3 || exercise 7.3 class 9 maths || chapter 7 exercise 7.3 class 9
2. \( \mathrm{AD}\) is an altitude of an isosceles triangle \(
\mathrm{ABC}\) in which \( \mathrm{AB}=\mathrm{AC} \). Show
that
(i) \( \mathrm{AD}\) bisects \( \mathrm{BC}\) (ii) \( \mathrm{AD}\) bisects \( \mathrm{A}\) .
(i) \( \mathrm{AD}\) bisects \( \mathrm{BC}\) (ii) \( \mathrm{AD}\) bisects \( \mathrm{A}\) .
Answer
It is given that \( A D \) is an altitude and \( A B=A C \). The
diagram is as follows: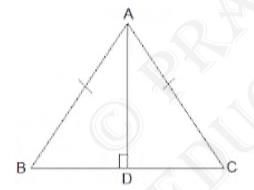
(i) In \( \triangle \mathrm{ABD} \) and \( \triangle \mathrm{ACD} \),
\( \mathrm{ADB}=\mathrm{ADC}=90^{\circ} \)
\( \mathrm{AB}=\mathrm{AC} \) (It is given in the question)
\( \mathrm{AD}=\mathrm{AD} \) (Common arm)
\( \therefore \triangle \mathrm{ABD} \triangle \mathrm{ACD} \) by RHS congruence condition.
Now, by the rule of CPCT,
\( \mathrm{BD}=\mathrm{CD} \).
So, \( \mathrm{AD}\) bisects \( \mathrm{BC}\)
(ii) Again, by the rule of \( \mathrm{CPCT}, \mathrm{BAD}=\mathrm{CAD} \)
Hence, \( \mathrm{AD}\) bisects \( \mathrm{BC}\).
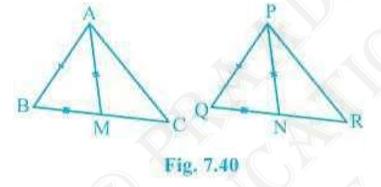
3. Two sides \( A B \) and \( B C \) and median \( A M \) of one
triangle \( A B C \) are respectively equal to sides \( P Q \) and
\( Q R \) and median \( P N \) of \( \triangle P Q R \) (see Fig.
7.40). Show that:
(i) \( \triangle \mathrm{ABM} \cong \triangle \mathrm{PQN} \)
(ii) \( \triangle \mathrm{ABC} \cong \triangle \mathrm{PQR} \)
(i) \( \triangle \mathrm{ABM} \cong \triangle \mathrm{PQN} \)
(ii) \( \triangle \mathrm{ABC} \cong \triangle \mathrm{PQR} \)

Answer
Given parameters are:\( \mathrm{AB}=\mathrm{PQ} \),
\( \mathrm{BC}=\mathrm{QR} \) and
\( \mathrm{AM}=\mathrm{PN} \)
(i) \( \frac{1}{2} \mathrm{BC}=\mathrm{BM} \) and \( \frac{1}{2} \mathrm{QR}=\mathrm{QN} \quad \) (Since AM and PN are medians)
Also, \( \mathrm{BC}=\mathrm{QR} \)
So, \( \frac{1}{2} \mathrm{BC}=\frac{1}{2} \mathrm{QR} \)
\( \Rightarrow \mathrm{BM}=\mathrm{QN} \)
In \( \triangle \mathrm{ABM} \) and \( \triangle \mathrm{PQN} \),
\( \mathrm{AM}=\mathrm{PN} \) and \( \mathrm{AB}=\mathrm{PQ} \) (As given in the question)
\( \mathrm{BM}=\mathrm{QN} \) (Already proved)
\( \therefore \triangle \mathrm{ABM} \triangle \mathrm{PQN} \) by SSS congruency.
(ii) In \( \triangle \mathrm{ABC} \) and \( \triangle \mathrm{PQR} \),
\( \mathrm{AB}=\mathrm{PQ} \) and \( \mathrm{BC}=\mathrm{QR} \) (As given in the question)
\( \mathrm{ABC}=\mathrm{PQR} \) (by CPCT)
So, \( \triangle \mathrm{ABC} \triangle \mathrm{PQR} \) by SAS congruency.
4. \( \mathrm{BE}\) and \( \mathrm{CF}\) are two equal altitudes
of a triangle \( \mathrm{ABC}\) . Using RHS congruence rule, prove
that the triangle \( \mathrm{ABC}\) is isosceles.
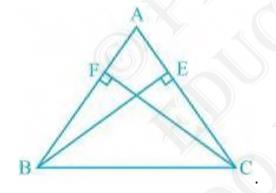

Answer
It is known that \( \mathrm{BE}\) and \( \mathrm{CF}\) are two
equal altitudes.Now, in \( \triangle \mathrm{BEC} \) and \( \triangle \mathrm{CFB} \),
\(\mathrm{BEC} =\mathrm{CFB}=90^{\circ} (\text { Same Altitudes })\)
\(\mathrm{BC} =\mathrm{CB} (\text { Common side })\)
\(\mathrm{BE} =\mathrm{CF} (\text { Common side })\)
So, \( \triangle \mathrm{BEC} \triangle \mathrm{CFB} \) by RHS congruence criterion.
Also, \( \mathrm{C}=\mathrm{B} \) (by CPCT)
Therefore, \( \mathrm{AB}=\mathrm{AC} \) as sides opposite to the equal angles is always equal.
5. \( \mathrm{ABC}\) is an isosceles triangle with \(
\mathrm{AB}=\mathrm{AC} \). Draw \( \mathrm{AP} \perp \mathrm{BC}
\) to show that \( \mathrm{B}=\mathrm{C}\).
Answer
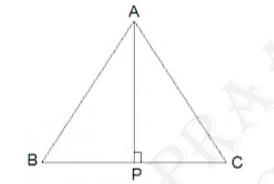
In the question, it is given that \( A B=A C \)
Now, \( \triangle \mathrm{ABP} \) and \( \triangle \mathrm{ACP} \) are similar by RHS congruency as
\( \mathrm{APB}=\mathrm{APC}=90^{\circ} \) (\( \mathrm{AP}\) is altitude)
\( \mathrm{AB}=\mathrm{AC} \) (Given in the question)
\( \mathrm{AP}=\mathrm{AP} \) (Common side)
So, \( \triangle \mathrm{ABP} \triangle \mathrm{ACP} \).
\( \therefore \mathrm{B}=\mathrm{C} \) (by CPCT)

