Miscellaneous Exercise On Chapter 6 Class 12

Let us consider \( y=x^{\frac{1}{4}} \) and \( x=\left(\frac{16}{81}\right) \) and \( \Delta x=\frac{1}{81} \)
Then, \( \Delta y=(x+\Delta x)^{\frac{1}{4}}-x^{\frac{1}{4}} \)
\( =\left(\frac{17}{81}\right)^{\frac{1}{4}}-\left(\frac{16}{81}\right)^{\frac{1}{4}} \)
\(=\left(\frac{17}{81}\right)^{\frac{1}{4}}-\frac{2}{3}\)
Therefore, \( \left(\frac{17}{81}\right)^{\frac{1}{4}}=\frac{2}{3}+\Delta y \)
Now, dy is approximately equal to \( \Delta y \) and is equal to
\(\mathrm{dy}=\left(\frac{d y}{d x}\right) \Delta x=\frac{1}{4(x)^{\frac{3}{4}}}(\Delta x)\)
\(=\frac{1}{4\left(\frac{16}{81}\right)^{\frac{3}{4}}}\left(\frac{1}{81}\right)=\frac{27}{4 \times 8}=\frac{1}{32 \times 3}=\frac{1}{96}=0.010\)
Therefore, the approximate value of \( \left(\frac{17}{81}\right)^{\frac{1}{4}} \) is \( \frac{2}{3}+0.010=0.677 \).

Let us consider \( y=(x)^{\frac{1}{5}} \) and \( x=32 \) and \( \Delta x=1 \)
Then, \( \Delta y=(x+\Delta x)^{\frac{1}{5}-x \frac{1}{5}} \)
\( =(33)^{\frac{1}{5}}-(32)^{\frac{1}{5}} \)
\( =(33)^{\frac{1}{5}}-\frac{1}{2} \)
Therefore,
\( (33)^{\frac{1}{5}}=\frac{1}{2}+\Delta y \)
Now, dy is approximately equal to \( \Delta y \) and is equal to
\( \mathrm{dy}=\left(\frac{d y}{d x}\right) \Delta x=\frac{-1}{5(x)^{\frac{6}{5}}}(\Delta x) \)
\( =\frac{-1}{5(2)^{6}}=\frac{-1}{320}=-0.003 \)
Therefore, the approximate value of \( (33)^{\frac{1}{5}} \) is \( \frac{1}{2}+(-0.003)=0.497 \)

It is given that \( \mathrm{f}(x)=\frac{\log x}{x} \)
Then, \( \mathrm{f}^{\prime}(x)=\frac{x\left(\frac{1}{x}\right)-\log x}{x^{2}}=\frac{1-\log x}{x^{2}} \)
Now, \( \mathrm{f}^{\prime}(x)=0 \)
\(\Rightarrow 1-\log x=0\)
\(\Rightarrow \log x=1\)
\(\Rightarrow \log x=\log \mathrm{e}\)
\(\Rightarrow x=\mathrm{e}\)
Now, \( \mathrm{f}^{\prime}(x)=\frac{x^{2}\left(\frac{-1}{x}\right)-(1-\log x)(2 x)}{x^{4}} \)
\(=\frac{-x-2 x(1-\log x)}{x^{4}}\)
\(=\frac{-3+2 \log x}{x^{3}}\)
Now, \( \mathrm{f}^{\prime} \) '(e) \( =\frac{-3+2 \text { loge }}{e^{3}}=\frac{-3+2}{e^{3}}=\frac{-1}{e^{3}} < 0 \)
Therefore, by second derivative test, \( f \) is the maximum at \( x=e \).

Let \( \triangle \mathrm{ABC} \) be isosceles where BC is the base of fixed length \( b \).
Let the length of the two equal sides of \( \triangle \mathrm{ABC} \) be a.
Now, draw a perpendicular AD to BC . Then, we have In \( \triangle \mathrm{ADC} \), by using Pythagoras theorem,
\(\mathrm{AD}=\sqrt{a^{2}-\frac{b^{2}}{4}}\)
Then, Area of triangle \( (\mathrm{A})=\frac{1}{2} b \sqrt{a^{2}-\frac{b^{2}}{4}} \)
The rate of change of the area with respect to time \( (\mathrm{t}) \) is given by: \( \frac{d A}{d t}=\frac{1}{2} \mathrm{~b} \frac{2 a}{\sqrt{a^{2}-\frac{b^{2}}{4}}} \frac{d a}{d t}=\frac{a b}{\sqrt{4 a^{2}-b^{2}}} \frac{d a}{d t} \)
It is given that the two equal sides of the triangle are decreasing at the rate of 3 cm per second.
\(\frac{d a}{d t}=-3 \mathrm{~cm} / \mathrm{s}\)
Then
\(\frac{d A}{d t}=\frac{-3 a b}{\sqrt{4 a^{2}-b^{2}}}\)
And when \( \mathrm{a}=\mathrm{b} \) we have,
\(\frac{d A}{d t}=\frac{-3 a b}{\sqrt{4 a^{2}-b^{2}}}=\frac{-3 b^{2}}{\sqrt{3 b^{2}}}=-\sqrt{3} b\)
Therefore, if the two sides are equal to the base, then the area of the triangle is decreasing at the rate of \( \sqrt{3} \mathrm{~b} \mathrm{~cm}^{2} / \mathrm{s} \).

It is given that curve is \( y^{2}=4 x \).
Differentiating with respect to \(x \), we get,
\(2 y \frac{d y}{d x}=4\)
\(\Rightarrow \frac{d y}{d x}=\frac{4}{2 y}=\frac{2}{y}\)
\(\left.\therefore \frac{d y}{d x}\right]_{(1,2)}=\frac{2}{2}=1\)
Now, the slope of the normal at point \( (1,2) \) is \( \frac{-1}{\left.\frac{d y}{d x}\right]_{(1,2)}}=\frac{-1}{1}=-1 \)
Therefore, Equation of the normal at \( (1,2) \) is \( y-2=-1(x-1) \)
\(\Rightarrow y-2=-x+1\)
\(\Rightarrow x+y-3=0\)

We have \( x=\mathrm{a} \cos \theta+\mathrm{a} \theta \sin \theta \),
\(\Rightarrow \frac{d x}{d \theta}=-\mathrm{a} \sin \theta+\mathrm{a} \sin \theta+\mathrm{a} \theta \cos \theta=\mathrm{a} \theta \cos \theta\)
And \( y=\operatorname{asin} \theta-a \theta \cos \theta \)
\(\Rightarrow \frac{d y}{d \theta}=\mathrm{a} \cos \theta-\mathrm{a} \cos \theta+\mathrm{a} \theta \cos \theta=\mathrm{a} \theta \cos \theta\)
So, \( \frac{d y}{d x}=\frac{d y}{d \theta} \cdot \frac{d \theta}{d x}=\frac{a \theta \sin \theta}{a \theta \cos \theta}=\tan \theta \)
Then, Slope of the normal at any point \( \theta \) is \( \frac{-1}{\tan \theta} \).
The equation of the normal at a given point \( (x, y) \) is:
\( y-\mathrm{asin} \theta+\mathrm{a} \theta \cos \theta=\frac{-1}{\tan \theta}(x-\mathrm{a} \cos \theta-\mathrm{a} \theta \sin \theta) \)
\( \Rightarrow y \sin \theta-\mathrm{asin}^{2} \theta+\mathrm{a} \theta \sin \theta \cos \theta=-x \cos \theta+\mathrm{acos}^{2} \theta+\mathrm{a} \theta \sin \theta \cos \theta \)
\( \Rightarrow x \cos \theta+y \sin \theta-\mathrm{a}\left(\sin ^{2} \theta+\cos ^{2} \theta\right)=0 \)
\( \Rightarrow x \cos \theta+y \sin \theta-\mathrm{a}=0 \)
Now, the perpendicular distance of the normal from the origin is \( \frac{|-a|}{\sqrt{\cos ^{2} \theta+sin^{2} \theta}}=\frac{|-a|}{\sqrt{1}}=|-\mathrm{a}| \), which is independent of \( \theta \).
Therefore, the perpendicular distance of the normal from the origin is constant.

(i) It is given that \( \mathrm{f}(x)=\frac{4 \sin x-2 x-x \cos x}{2+\cos x} \)
\(\therefore f^{\prime}(x)\)
\(=\frac{(2+\cos x)(4 \cos x-2-\cos x+x \sin x)-(4 \sin x-2 x-x \cos x)(-\sin x)}{(2+\cos x)^{2}}\)
\(=\frac{(2+\cos x)(3 \cos x-2-x \sin x)+\sin x(4 \sin x-2 x-x \cos x)}{(2+\cos x)^{2}}\)
\(=\frac{6 \cos x-4+2 x \sin x+3 \cos ^{2} x-2 \cos x+x \sin x \cos x+4 \sin ^{2} x-2 x \sin x-x \sin x \cos x}{(2+\cos x)^{2}}\)
\(=\frac{4 \cos x-4+3 \cos ^{2} x+4 \sin ^{2} x}{(2+\cos x)^{2}}\)
\(=\frac{4 \cos x-4+3 \cos ^{2} x+4-4 \cos ^{2} x}{(2+\cos x)^{2}}\)
\(=\frac{4 \cos x-\cos ^{2} x}{(2+\cos x)^{2}}\)
\(=\frac{\cos x(4-\cos x)}{(2+\cos x)^{2}}\)
Now, if \(\mathrm{f}^\prime(x)=0\)
\(\Rightarrow \cos x=0 \text { or } \cos x=4\)
But, \( \cos x=4 \) is not possible
Therefore, \( \cos x=0 \)
\(\Longrightarrow x=\frac{\pi}{2}, \frac{3 \pi}{2}\)
Now, \( x=\frac{\pi}{2}, \frac{3 \pi}{2} \) divides \( (0,2 \pi) \) into three disjoints intervals \( \left(0, \frac{\pi}{2}\right),\left(\frac{\pi}{2}, \frac{3 \pi}{2}\right) \) and \( \left(\frac{3 \pi}{2}, 2 \pi\right) \)
In the intervals \( \left(0, \frac{\pi}{2}\right) \) and \( \left(\frac{3 \pi}{2}, 2 \pi\right), \mathrm{f}^{\prime}(x) > 0 \)
Therefore, \( f(x) \) is increasing for \( 0 < x < \frac{\pi}{2} \) and \( \frac{3 \pi}{2} < x < 2 \pi \).
In interval \( \left(\frac{\pi}{2}, \frac{3 \pi}{2}\right), \mathrm{f}^{\prime}(x) < 0 \)
Therefore, \( \mathrm{f}(x) \) is decreasing for \( \frac{\pi}{2} < x < \frac{3 \pi}{2} \).

It is given that \( \mathrm{f}(x)=x^{3}+\frac{1}{x^{3}} \)
\(\therefore f^{\prime}(x)=3 x^{2}-\frac{3}{x^{4}}=\frac{3 x^{6}-3}{x^{4}}\)
Then, \( \mathrm{f}^{\prime}(x)=0 \)
\(\Rightarrow 3 x^{6}-3=0\)
\(\Rightarrow x^{6}=1\)
\(\Rightarrow x= \pm 1\)
Now, the points \( x=1 \) and \( x=-1 \) divide the real line into three disjoint intervals
\( (-\infty,-1),(-1,1) \) and \( (1, \infty) \).
In interval \( (-\infty,-1) \) and \( (1, \infty) \) when \( x < -1 \) and \( x > 1 \) then \( \mathrm{f}^{\prime}(x) > 0 \)
Therefore, when \( x < -1 \) and \( x > 1 \), f is increasing.
And, in interval \( (-1,1) \) when \( -1 < x < 1 \) then \( \mathrm{f}^{\prime}(x) < 0 \).
Therefore, when \( -1 < x < 1 \), f is decreasing.

It is given that ellipse \( \frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1 \)
Let the major axis be along the \( x- \) axis.1).
Let ABC be the triangle inscribed in the ellipse where vertex C is at \( (a, 0) \).
Since, the ellipse is symmetrical w.r.t. \(x\) - axis and \(y\) - axis, we can assume the coordinates of A to be \( \left(-x_{1}, y_{1}\right) \) and the coordinates of B to be \( \left(-x_{1},-y_{1}\right) \).
Now, we have \( y_{1}= \pm \frac{b}{a} \sqrt{a^{2}-x_{1}^{2}} \)
Therefore, Coordinates of A \( \left(-x_{1}, \frac{b}{a} \sqrt{a^{2}-x_{1}^{2}}\right) \) and the coordinates of B \( \left(-x_{1},-\frac{b}{a} \sqrt{a^{2}-x_{1}^{2}}\right) \)
As the point \( \left(x_{1}, y_{1}\right) \) lies on the ellipse, the area of triangle \( A B C(A) \) is given by:
\(\mathrm{A}=\frac{1}{2}\left|a\left(\frac{2 b}{a} \sqrt{a^{2}-x_{1}^{2}}\right)+\left(-x_{1}\right)\left(-\frac{b}{a} \sqrt{a^{2}-x_{1}^{2}}\right)+\left(-x_{1}\right)\left(-\frac{b}{a} \sqrt{a^{2}-x_{1}^{2}}\right)\right|\)
\(\Rightarrow \mathrm{A}=\mathrm{b} \sqrt{a^{2}-x_{1}^{2}}+x_{1} \frac{b}{a} \sqrt{a^{2}-x_{1}^{2}} \ldots \ldots .(1)\)
\(\therefore \frac{d A}{d x_{1}}=\frac{-2 x_{1} b}{2 \sqrt{a^{2}-x_{1}^{2}}}+\frac{b}{a} \sqrt{a^{2}-x_{1}^{2}}-\frac{2 b x_{1}^{2}}{a^{2} \sqrt{a^{2}-x_{1}^{2}}}\)
\(=\frac{b}{a^{2} \sqrt{a^{2}-x_{1}^{2}}}\left[-x_{1} a+\left(a^{2}-x_{1}^{2}\right)-x_{1}^{2}\right]\)
\(=\frac{b\left(-2 x_{1}^{2}-x_{1}+a^{2}\right)}{a \sqrt{a^{2}-x_{1}^{2}}}\)
\(\text { Now, } \frac{d A}{d x_{1}}=0\)
\(\Rightarrow-2 x_{1}^{2}-x_{1} a+a^{2}=0\)
\(\Rightarrow x_{1}=\frac{a \pm \sqrt{a^{2}-4(-2)\left(a^{2}\right)}}{2(-2)}\)
\(=\frac{a \pm \sqrt{9 a^{2}}}{-4}\)
\(=\frac{a \pm 3 a}{-4}\)
\(\Rightarrow x_{1}=-\mathrm{a}, \frac{a}{2}\)
But, \( x_{1} \) cannot be equal to a.
\(\Rightarrow x_{1}=\frac{a}{2}\)
\(y_{1}=\frac{b}{a} \sqrt{a^{2}-\frac{a^{2}}{4}}=\frac{b a}{2 a} \sqrt{3}=\frac{\sqrt{3 t}}{2}\)
Now, \( \frac{d^{2} A}{d x_{1}^{2}}=\frac{b}{a}\left\{\frac{\sqrt{a^{2}-x_{1}^{2}\left(-4 x_{1}-a\right)-\left(-2 x_{1}^{2}-x_{1} a+a^{2}\right) \frac{\left(-2 x_{1}\right)}{\sqrt[2]{a^{2}-x_{1}^{2}}}}}{a^{2}-x_{1}^{2}}\right\} \)
\(=\frac{b}{a}\left\{\frac{\left(a^{2}-x_{1}^{2}\right)\left(-4 x_{1}-a\right)+x_{1}\left(-2 x_{1}^{2}-x_{1} a+a^{2}\right)}{\left(a^{2}-x_{1}^{2}\right)^{\frac{3}{2}}}\right\}\)
\(=\frac{b}{a}\left\{\frac{2 x^{3}-3 a^{2} x-a^{3}}{\left(a^{2}-x_{1}^{2}\right)^{\frac{3}{2}}}\right\}\)
Also, when \( x_{1}=\frac{a}{2} \), then,
\(\frac{d^{2} A}{d x_{1}^{2}}=\frac{b}{a}\left\{\frac{2 \frac{a^{3}}{8}-3 \frac{a^{3}}{2}-a^{3}}{\left(\frac{3 a}{4}\right)^{\frac{3}{2}}}\right\}\)
\(=\frac{b}{a}\left\{\frac{\frac{a^{3}}{4}-\frac{3 a^{3}}{2}-a^{3}}{\left(\frac{3 a}{4}\right)^{\frac{3}{2}}}\right\}\)
\(=\frac{b}{a}\left\{\frac{\frac{9 a^{3}}{4}}{\left(\frac{3 a}{4}\right)^{\frac{3}{2}}}\right\} < 0\)
Then, the area is the maximum when \( x_{1}=\frac{a}{2} \).
Therefore, Maximum area of the triangle is given by:
\(\mathrm{A}=b \sqrt{a^{2}-\frac{a^{2}}{4}}+\left(\frac{a}{2}\right) \frac{b}{a} \sqrt{a^{2}-\frac{a^{2}}{4}}\)
\(=\mathrm{ab} \frac{\sqrt{3}}{2}+\left(\frac{a}{2}\right) \frac{b}{a} \times \frac{a \sqrt{3}}{2}\)
\(=\frac{a b \sqrt{3}}{2}+\frac{a b \sqrt{3}}{4}\)
\(=\frac{3 \sqrt{3}}{4} \mathrm{ab}\)

Let \( \mathrm{l}, \mathrm{b} \), and h be the length, breadth and height of the tank respectively.
then, we have \( \mathrm{h}=2 \mathrm{~m} \)
Volume of the tank \( =8 \mathrm{~m}^{3} \)
Volume of the tank \( =1 \times \mathrm{b} \times \mathrm{h} \)
\(\Rightarrow 8=1 \times \mathrm{b} \times 2\)
\(\Rightarrow \mathrm{lb}=4\)
\(\Rightarrow \mathrm{b}=\frac{4}{1}\)
Now, area of the base \( =1 b=4 \)
Area of the 4 walls \( (A)=2 h(1+b) \)
\(\therefore \mathrm{A}=4\left(1-\frac{4}{I^{2}}\right)\)
Now, \( \frac{d A}{d l}=0 \)
\(\Rightarrow 1-\frac{4}{I^{2}}=0\)
\(\Rightarrow l^{2}=4\)
\(\Rightarrow l= \pm 2\)
Since, length cannot be negative therefore \( l=2 \).
\(\Rightarrow b=2\)
Now, \( \frac{d^{2} A}{d l^{2}}=\frac{32}{1^{3}} \)
When \( l=2 \),
\(\frac{d^{2} A}{d l^{2}}=\frac{32}{8}=4 > 0\)
Then, by second derivative test, the area is the minimum when \( l=2 \).
We have, \( l=\mathrm{b}=\mathrm{h}=2 \)
Therefore, Cost of building the base \( = \) Rs \( 70 \times(\mathrm{lb})= \) Rs \( 70(4)= \) Rs 280 .
Cost of building the walls \( = \) Rs \( 2 \mathrm{~h}(l+\mathrm{b}) \times 45= \) Rs \( 90(2)(2+2) \) \( = \) Rs \( 8(90)= \) Rs 720 .
Required total cost \( =\operatorname{Rs}(280+720)= \) Rs 1000.
Therefore, the total cost of the tank will be Rs 1000 .

Let \( r \) be the radius of the circle and a be the side of the square.
Then, \( 2 \pi \mathrm{r}+4 \mathrm{a}=\mathrm{k} \) (where k is constant)
\(\Rightarrow \mathrm{a}=\frac{k-2 \pi r}{4}\)
The sum of the areas of the circle and square \( (\mathrm{A}) \) is
\(=\pi \mathrm{r}^{2}+\mathrm{a}^{2}=\pi \mathrm{r}^{2}+\left(\frac{k-2 \pi r}{4}\right)^{2}\)
\(\therefore \frac{d A}{d r}=2 \pi r+\frac{2(k-2 \pi r)(-2 \pi)}{16}=2 \pi r-\frac{\pi(k-2 \pi r)}{4}\)
Now, \( \frac{d A}{d r}=0 \)
\(\Rightarrow 2 \pi r=\frac{\pi(k-2 \pi r)}{4}\)
\(8 \mathrm{r}=\mathrm{k}-2 \pi \mathrm{r}\)
\(\Rightarrow(8+2 \pi) \mathrm{r}=\mathrm{k}\)
\(\Rightarrow \mathrm{r}=\frac{k}{8+2 \pi}=\frac{k}{2(4+\pi)}\)
Now, \( \frac{d^{2} A}{d r^{2}}=2 \pi+\frac{\pi^{2}}{2} > 0 \)
Therefore, When \( \mathrm{r}=\frac{k}{2(4+\pi)}, \frac{d^{2} A}{d r^{2}} > 0 \)
\( \Rightarrow \) The sum of the area is least when \( \mathrm{r}=\frac{k}{2(4+\pi)} \)
So, when \( \mathrm{r}=\frac{k}{2(4+\pi)} \)
Then \( \mathrm{a}=\frac{k-2 \pi\left[\frac{k}{2(4+\pi)}\right]}{4}=2 \mathrm{r} \)
Therefore, it is proved that the sum of their areas is least when the side of the square is double the radius of the circle.

Let \(x\) and \(y\) be the length and breadth of the rectangular window.
Radius of the semi - circular opening \( =\frac{x}{2} \)
It is given that the perimeter of the window is 10 m .
\(\Rightarrow x+2 y+\frac{\pi x}{2}=10\)
\(\Rightarrow x\left(1+\frac{\pi}{2}\right)+2 y=10\)
\(\Rightarrow 2 y=10-x\left(1+\frac{\pi}{2}\right)\)
\(\Rightarrow y=5-x\left(\frac{1}{2}+\frac{\pi}{4}\right)\)
Therefore, Area of the window (A) is given by
\(=xy+\frac{\pi}{2}\left(\frac{x}{y}\right)^{2}\)
\(=xy+\frac{\pi}{2}\left(\frac{x}{y}\right)^{2}\)
\(=x\left[5-x\left(\frac{1}{2}+\frac{\pi}{4}\right)\right]+\frac{\pi x^{2}}{8}\)
\(=5 x-x^{2}\left(\frac{1}{2}+\frac{\pi}{4}\right)+\frac{\pi x^{2}}{8}\)
\(\therefore \frac{d A}{d x}=5-2 x\left(\frac{\pi}{4}+\frac{1}{2}\right)+\frac{\pi}{4} x\)
\(=5-x\left(1+\frac{\pi}{2}\right)+\frac{\pi}{4} x\)
\(\therefore \frac{d^{2} A}{d x^{2}}=-\left(1+\frac{\pi}{2}\right)+\frac{\pi}{4}=-1-\frac{\pi}{4}\)
Now, \( \frac{d A}{d x}=0 \), then
\(\Rightarrow 5-x\left(1+\frac{\pi}{2}\right)+\frac{\pi}{4} x=0\)
\(\Rightarrow 5-x-\frac{\pi}{4} x=0\)
\(\Rightarrow x\left(1+\frac{\pi}{4}\right)=5\)
\(\Rightarrow x=\frac{5}{\left(1+\frac{\pi}{4}\right)}=\frac{20}{\pi+4}\)
Then, when \( x=\frac{20}{\pi+4} \) then \( \frac{d^{2} A}{d x^{2}} < 0 \).
Therefore, by second derivative test, the area is maximum when length \( x=\frac{20}{\pi+4} \mathrm{~m} \).
Now, \( y=5-\frac{20}{\pi+4}\left(\frac{2+\pi}{4}\right)=6=5-\frac{5(2+\pi)}{4}=\frac{10}{\pi+4} \mathrm{~m} \)
Therefore, the required dimensions of the window to admit maximum light is given by length \( =\frac{20}{\pi+4} \mathrm{~m} \) and breadth \( =\frac{20}{\pi+4} \mathrm{~m} \).

Let \( \triangle \mathrm{ABC} \) be right - angled at B . Let \( \mathrm{AB}=x \) and \( \mathrm{BC}=y \).
Let P be a point on the hypotenuse of the triangle such that P is at a distance of a and b from the sides AB and Bc respectively.
Let \( < \mathrm{C}=\theta \).
Now, we have,
\( \mathrm{AC}=\sqrt{x^{2}+y^{2}} \)
Now, \( \mathrm{PC}=\mathrm{b} \operatorname{cosec} \theta \)
And \( \mathrm{AP}=\mathrm{a} \sec \theta \)
\( \Rightarrow \mathrm{AC}=\mathrm{AP}+\mathrm{PC} \)
\( \Rightarrow \mathrm{AC}=\mathrm{a} \sec \theta+\mathrm{b} \operatorname{cosec} \theta \)
\(\therefore \frac{d(A C)}{d \theta}=-\mathrm{b} \operatorname{cosec} \theta+\mathrm{asec} \theta \cot \theta\)
Now, if \( \frac{d(A C)}{d \theta}=0 \)
\(\Rightarrow a \sec \theta \tan \theta=b \operatorname{cosec} \theta \cot \theta\)
\(\Rightarrow \frac{a}{\cos \theta} \cdot \frac{\sin \theta}{\cos \theta}=\frac{a}{\sin \theta} \cdot \frac{\cos \theta}{\sin \theta}\)
\(\Rightarrow a \sin^{3} \theta=b \cos ^{3} \theta\)
\(\Rightarrow(a)^{\frac{1}{3}} \sin \theta=(b)^{\frac{1}{3}} \sin \theta\)
\(\Rightarrow \tan \theta=\left(\frac{b}{a}\right)^{\frac{1}{3}}\)
\(\therefore \sin \theta=\frac{(b)^{\frac{1}{3}}}{\sqrt{a^{\frac{2}{3}}+b^{\frac{2}{3}}}} \text { and } \cos \theta=\frac{(a)^{\frac{1}{3}}}{\sqrt{a^{\frac{2}{3}}+b^{\frac{2}{3}}}}\ldots(1)\)
So, it is clear that \( \frac{d^{2} A}{d \theta^{2}} < 0 \) when \( \tan \theta=\left(\frac{b}{a}\right)^{\frac{1}{3}} \)
Therefore, by second derivative test, the length of the hypotenuse is the maximum when \( \tan \theta=\left(\frac{b}{a}\right)^{\frac{1}{3}} \)
Now, when \( \tan \theta=\left(\frac{b}{a}\right)^{\frac{1}{3}} \), we get,
\(\operatorname{Ac}=\frac{b \sqrt{a^{\frac{2}{3}}+b^{\frac{2}{3}}}}{(b)^{\frac{1}{3}}}+\frac{a \sqrt{a^{\frac{2}{3}}+b^{\frac{2}{3}}}}{(a)^{\frac{1}{3}}}\)
\( =\sqrt{a^{\frac{2}{3}}+b^{\frac{2}{3}}}\left(b^{\frac{2}{3}}+a^{\frac{2}{3}}\right) \)
\( =\left(a^{\frac{2}{3}}+b^{\frac{2}{3}}\right)^{\frac{3}{2}} \)
Therefore, the maximum length of the hypotenuses is \( \left(a^{\frac{2}{3}}+b^{\frac{2}{3}}\right)^{\frac{3}{2}} \).

It is given that function is \( f(x)=(x-2)^{4}(x+1)^{3} \)
\(\Rightarrow f^{\prime}(x)=4(x-2)^{3}(x+1)^{3}+3(x+1)^{2}(x-2)^{4}\)
\(=(x-2)^{3}(x+1)^{2}[4(x+1)+3(x-2)]\)
\(=(x-2)^{3}(x+1)^{2}(7 x-2)\)
Now, \( f^{\prime}(x)=0 \)
\( \Rightarrow x=-1 \) and \( x=\frac{2}{7} \) or \( x=2 \)
Now, for values of \( x \) close to \( \frac{2}{7} \) and to the left of \( \frac{2}{7} \)
\(f^{\prime}(x) > 0\)
Also, for values of \( x \) close to \( \frac{2}{7} \) and to the right of \( \frac{2}{7}, f^{\prime}(x) < 0 \).
Then, \( x=\frac{2}{7} \) is the point of local maxima.
Now, for values of \( x \) close to 2 and to the left of \( 2, f^{\prime}(x) < 0 \).
Also, for values of \( x \) close to 2 and to the right of \( 2 . f^{\prime}(x) > 0 \).
Then, \( x=2 \) is the point of local minima.
Now, as the value of \(x\) varies through - \( 1, \mathrm{f}^{\prime}(x) \) does not changes its sign.
Then, \( x=-1 \) is the point of inflexion.

It is given that \( f(x)=\cos ^{2} x+\sin x, x \in[0, \pi] \)
\(f^{\prime}(x)=2 \cos x(-\sin x)+\cos x\)
\(=-2 \sin x \cos x+\cos x\)
Now, if \( f^{\prime}(x)=0 \)
\( \Rightarrow 2 \sin x \cos x=\cos x \)
\( \Rightarrow \cos x(2 \sin x-1)=0 \)
\( \Rightarrow \sin x=\frac{1}{2} \) or \( \cos x=0 \)
\( \Rightarrow x=\frac{\pi}{6} \), or \( \frac{\pi}{2} \) as \( x \in[0, \pi] \)
Now, evaluating the value of \( f \) at critical points \( x=\frac{\pi}{2} \) and \( x=\frac{\pi}{6} \) and at the end points of the interval \( [0, \pi] \), (ie, at \( x=0 \) and \( x=\pi \) ), we get,
\(\mathrm{f}\left(\frac{\pi}{6}\right)=\cos ^{2} \frac{\pi}{6}+\sin \frac{\pi}{6}=\left(\frac{\sqrt{3}}{2}\right)^{2}+\frac{1}{2}=\frac{5}{4}\)
\(\mathrm{f}(0)=\cos ^{2} 0+\sin 0=1+0=1\)
\(\mathrm{f}(\pi)=\cos ^{2} \pi+\sin \pi=(-1)^{2}+0=1\)
\(\mathrm{f}\left(\frac{\pi}{2}\right)=\cos ^{2} \frac{\pi}{2}+\sin \frac{\pi}{2}=0+1=1\)
Therefore, the absolute maximum value of f is \( \frac{5}{4} \) occurring at \( x=\frac{\pi}{6} \) and the absolute minimum value of f is 1 occuring at \( x=1, \frac{\pi}{2} \) and \( \pi \).

Let R and h be the radius and the height of the cone respectively.

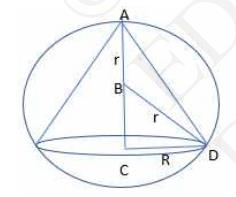
The volume \( (\mathrm{V}) \) of the cone is given by;
\(\mathrm{V}=\frac{1}{3} \pi r^{2} \mathrm{~h}\)
Now, from the right triangle BCD , we get,
\(\mathrm{BC}=\sqrt{r^{2}-R^{2}}\)
\(\therefore \mathrm{h}=\mathrm{r}+\sqrt{r^{2}-R^{2}}\)
\(\mathrm{~V}=\frac{1}{3} \pi r^{2} \mathrm{~h}\left(r+\sqrt{r^{2}-R^{2}}\right)\)
\(=\frac{1}{3} \pi r^{2} \mathrm{~h}+\frac{1}{3} \pi R^{2} \sqrt{r^{2}-R^{2}}\)
\(\frac{d V}{d R}=\frac{2}{3} \pi \mathrm{Rr}+\frac{2}{3} \pi \mathrm{R} \sqrt{r^{2}-R^{2}}+\frac{R^{3}}{3} \cdot \frac{(-2 R)}{2 \sqrt{r^{2}-R^{2}}}\)
\(=\frac{2}{3} \pi \mathrm{Rr}+\frac{2}{3} \pi \mathrm{R} \sqrt{r^{2}-R^{2}}+\frac{R^{3}}{3 \sqrt{r^{2}-R^{2}}}\)
\(=\frac{2}{3} \pi \mathrm{Rr}+\frac{2 \pi R\left(r^{2}-R^{2}\right)-\pi R^{3}}{3 \sqrt{r^{2}-R^{2}}}\)
\(=\frac{2}{3} \pi \mathrm{Rr}+\frac{2 \pi R r^{2}-3 \pi R^{3}}{3 \sqrt{r^{2}-R^{2}}}\)
Now, if \( \frac{d V}{d R}=0 \), then
\(\frac{2}{3} \pi \mathrm{Rr}=-\frac{2 \pi R r^{2}-3 \pi R^{3}}{3 \sqrt{r^{2}-R^{2}}}\)
\(\Rightarrow 2 \mathrm{r} \sqrt{r^{2}-R^{2}}=3 R^{2}-2 r^{2}\)
\(\Rightarrow 4 r^{2}\left(r^{2}-R^{2}\right)=\left(3 R^{2}-2 r^{2}\right)^{2}\)
\(\Rightarrow 4 r^{4}-4 r^{2} R^{2}=9 R^{4}+4 r^{4}-12 R^{2} r^{2}\)
\(\Rightarrow 9 R^{4}-8 r^{2} R^{2}=0\)
\(\Rightarrow 9 R^{2}=8 r^{2}\)
\(\Rightarrow R^{2}=\frac{8 r^{2}}{9}\)
Now, \( \frac{d^{2} V}{d R^{2}}=\frac{2 \pi r}{3}+\frac{3 \sqrt{r^{2}-R^{2}}\left(2 \pi r^{2}-9 \pi R^{2}\right)-\left(2 \pi R r^{2}-3 \pi R^{3}\right)(-6 R) \frac{1}{2 \sqrt{r^{2}-R^{2}}}}{9 \sqrt{r^{2}-R^{2}}} \)
Now, when \( R^{2}=\frac{8 r^{2}}{9} \), it can be shown that \( \frac{d^{2} V}{d R^{2}} < 0 \).
Therefore, the volume is the maximum when \( R^{2}=\frac{8 r^{2}}{9} \).
When \( R^{2}=\frac{8 r^{2}}{9} \),
Height of the cone \( =\mathrm{r}+\sqrt{r^{2}-\frac{8 r^{2}}{9}}=\mathrm{r}+\sqrt{\frac{r^{2}}{9}}=\mathrm{r}+\frac{r}{3}=\frac{4 r}{3} \).
Therefore, it can be seen that the altitude of the circular cone of maximum volume that can be inscribed in a sphere of radius \( r \) is \( \frac{4 r}{3} \).

Since, \( \mathrm{f}^{\prime}(x) > 0 \) on \( (\mathrm{a}, \mathrm{b}) \)
Then, f is a differentiating function \( (\mathrm{a}, \mathrm{b}) \)
Also, every differentiable function is continuous,
Therefore, \( f \) is continuous on \( [a, b] \)
Let \( x_{1}, x_{2} \epsilon(\mathrm{a}, \mathrm{b}) \) and \( x_{2} > x 1 \) then by LMV theorem, there exists \( \mathrm{c} \epsilon(\mathrm{a}, \mathrm{b}) \) s.t.
\( \mathrm{f}^{\prime}(\mathrm{c})=\frac{f\left(x_{2}-\mathrm{f}\left(x_{1}\right)\right)}{x_{2}-x_{2}} \)
\( =\mathrm{f}\left(x_{2}\right)-\mathrm{f}\left(x_{1}\right)=\left(x_{2}-x_{1}\right) \mathrm{f}^{\prime}(\mathrm{c}) \)
\(\Rightarrow \mathrm{f}\left(x_{2}\right)-\mathrm{f}\left(x_{1}\right) > 0 \text { as }\left(x_{2} < x_{1}\right) \mathrm{f}^{\prime}(\mathrm{c})\)
\(\Rightarrow \mathrm{f}\left(x_{2}\right)-\mathrm{f}\left(x_{1}\right) > 0 \text { as } x_{2} > x_{1} \text { and } \mathrm{f}^{\prime}(x) > 0\)
\(\Rightarrow \mathrm{f}\left(x_{1}\right) > \mathrm{f}\left(x_{2}\right)\)
\(\therefore \text { for } x_{1} < x_{2} \Rightarrow \mathrm{f}\left(x_{1}\right) < \mathrm{f}\left(x_{2}\right)\)
Therefore, f is an increasing function.

Let r and h be the radius and the height of the cylinder respectively.
Now, \( \mathrm{h}=2 \sqrt{R^{2}-r^{2}} \)
The volume \( (\mathrm{V}) \) of the cylinder is given by:
\(\mathrm{V}=\pi r^{2} \mathrm{~h}=2 \pi r^{2} \sqrt{R^{2}-r^{2}}\)
\(\frac{d V}{d r}=4 \pi r \sqrt{R^{2}-r^{2}}+\frac{2 \pi r^{2}(-2 r)}{2 \sqrt{R^{2}-r^{2}}}\)
\(=4 \pi r \sqrt{R^{2}-r^{2}}-\frac{2 \pi r^{3}}{\sqrt{R^{2}-r^{2}}}\)
\(=\frac{4 \pi r\left(R^{2}-r^{2}\right)-2 \pi r^{3}}{\sqrt{R^{2}-r^{2}}}\)
\(=\frac{4 \pi R^{2}-6 \pi r^{3}}{\sqrt{R^{2}-r^{2}}}\)
Now, if \( \frac{d V}{d r}=0 \Rightarrow 4 \pi R^{2}-6 \pi r^{3}=0 \)
\( \Longrightarrow r^{2}=\frac{2 R^{2}}{3} \)
Now, \( \frac{d^{2} V}{d r^{2}}=\frac{\sqrt{R^{2}-r^{2}}\left(4 \pi R^{2}-18 \pi r^{2}\right)-\left(4 \pi R^{2}-6 \pi r^{3}\right) \frac{(-2 r)}{2 \sqrt{R^{2}-r^{2}}}}{\left(R^{2}-r^{2}\right)} \)
\( =\frac{\left(R^{2}-r^{2}\right)\left(4 \pi R^{2}-18 \pi r^{2}\right)+\left(4 \pi R^{2}-6 \pi r^{3}\right)}{\left(R^{2}-r^{2}\right)^{\frac{3}{2}}} \)
\( =\frac{4 \pi R^{4}-22 r^{2} R^{2}+12 \pi r^{4}+4 \pi r^{2} R^{2}}{\left(R^{2}-r^{2}\right)^{\frac{3}{2}}} \)
Now, we can see that at \( r^{2}=\frac{2 R^{2}}{3}, \frac{d^{2} V}{d r^{2}} < 0 \).
Therefore, the volume is the maximum when \( r^{2}=\frac{2 R^{2}}{3} \).
When \( r^{2}=\frac{2 R^{2}}{3} \), the height of the cylinder is \( 2 \sqrt{R^{2}-\frac{2 R^{2}}{3}}=2 \sqrt{\frac{R^{2}}{3}}=\frac{2 R}{\sqrt{3}} \).
Therefore, the volume of the cylinder is the maximum when the height of the cylinder is \( \frac{2 R}{\sqrt{3}} \).
Hence Proved.

The figure is given below:

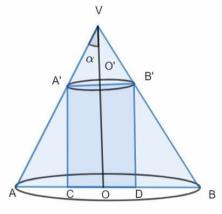
Let VAB be a given cone of height h , semi-vertical angle \( \alpha \) and let \( x \) be the radius of the base of the cylinder \( A^{\prime} B^{\prime} D C \) which is inscribed in the cone VAB.
In triangle \( \mathrm{VO}^{\prime} \mathrm{A}^{\prime} \),
\(\tan \alpha=\frac{\mathrm{O}^{\prime} \mathrm{A}^{\prime}}{\mathrm{VO}^{\prime}}=\frac{x}{\mathrm{VO}^{\prime}}\)
\( \mathrm{VO}^{\prime}=x \cot \alpha \)
\( \mathrm{OO}^{\prime}=\mathrm{VO}-\mathrm{VO}^{\prime}=\mathrm{h}-x \cot \alpha \)
Let V be the volume of the cylinder.
Then, \( \mathrm{V}=\pi\left(\mathrm{O}^{\prime} \mathrm{B}^{\prime}\right)^{2}\left(\mathrm{OO}^{\prime}\right) \)
\( \mathrm{V}=\pi x^{2}(\mathrm{~h}-x \cot \alpha) \)
Differentiating with respect to \(x \), we get,
\(\frac{d V}{d x}=2 \pi x h-3 \pi x^{2} \cot \alpha\)
Now, putting \( \mathrm{dV} / \mathrm{dx}=0 \), for maxima or minima, we get,
\( 2 \pi x h-3 \pi x^{2} \cot \alpha \)
\( x=\frac{2 h}{3} \tan t \alpha \)
Now, \( \frac{d^{2} V}{d x^{2}}=2 \pi \mathrm{h}-6 \pi x \cot \alpha \)
Putting the value of \( x \), we get,
\(\frac{d^{2} V}{d x^{2}}=\pi(2 h-4 h)=-2 \pi h < 0\)
Therefore, there is maxima at \( x=\frac{2 h}{3} \tan \alpha \) Hence, putting the value of \( x \), in formula of volume, we get,
\(\mathrm{V}=\pi\left(\frac{2 h}{3} \tan \alpha\right)^{2}\left(h-\frac{2 h}{3}\right)=\frac{4}{27} \pi h^{3} \tan ^{2} \alpha\)
And \( O O^{\prime}=\mathrm{h}-x \cot \alpha=\mathrm{h}-\frac{2 h}{3}=\frac{\mathrm{h}}{3}\)

Let V be the volume of the cylinder
\(
\mathrm{V}=\pi \mathrm{r}^{2} \mathrm{~h}\)
\(=\pi(10)^{2} \mathrm{~h}\)
\(\Rightarrow \mathrm{V}=100 \pi \mathrm{h}\)
Differentiating w.r.t. t we get,
\(\frac{d V}{d t}=100 \pi \frac{d h}{d t}\)
The tank is being filled with wheat at the rate of 314 cubic meter per hour.
\(\frac{d V}{d t}=314 \mathrm{~m}^{3} / \mathrm{h}\)
Then, we have,
\(314=100 \pi \frac{d h}{d t}\)
\(\Rightarrow \frac{d h}{d t}=\frac{314}{100 \times 3.14}=1\)
Therefore, the depth of wheat is increasing at the rate of \( 1 \mathrm{~m} / \mathrm{h} \).

It is given that curve \( x=\mathrm{t}^{2}+3 \mathrm{t}-8, y=2 \mathrm{t}^{2}-2 \mathrm{t}-5 \)
Then, \( \frac{d x}{d t}=2 \mathrm{t}+3 \) and \( \frac{d y}{d t}=4 \mathrm{t}-2 \)
\(\Rightarrow \frac{d y}{d x}=\frac{d y}{d t} \cdot \frac{d t}{d x}=\frac{4 \mathrm{t}-2}{2 t-3}\)
The given points is \( (2,-1) \)
At \( x=2 \), we get
\(\mathrm{t}^{2}+3 \mathrm{t}-8=2\)
\(\Rightarrow \mathrm{t}^{2}+3 \mathrm{t}-10=0\)
\(\Rightarrow(\mathrm{t}-2)(\mathrm{t}+5)=0\)
\(\Rightarrow \mathrm{t}=2 \text { and }-5\)
\(\text { At } y=-1 \text {, we get }\)
\(2 \mathrm{t}^{2}-2 \mathrm{t}-5=-1\)
\(\Rightarrow 2 \mathrm{t}^{2}-2 \mathrm{t}-4=0\)
\(\Rightarrow 2\left(\mathrm{t}^{2}-\mathrm{t}-2\right)=0\)
\(\Rightarrow(\mathrm{t}-2)(\mathrm{t}+1)=0\)
\(\Rightarrow \mathrm{t}=2 \text { and }-1\)
Therefore, the common value of \( t \) is 2 .
Hence, the slope of the tangent to the given curve at point \( (2,-1) \) is \( \left.\frac{d y}{d x}\right]_{t=2}=\frac{4(2)-2}{2(2)+3}=\frac{8-2}{4+3}=\frac{6}{7} \)

It is given that the equation of the tangent to the given curve is
\(y=m x+1\)
Now, substituting the value of \( y \) in \( y^{2}=4 x \), we get
\(\Rightarrow(\mathrm{mx}+1)^{2}=4 x\)
\(\Rightarrow \mathrm{m}^{2} x^{2}+1+2 \mathrm{mx}-4 x=0\)
\(\Rightarrow \mathrm{m}^{2} x^{2}+x(2 \mathrm{~m}-4)+1=0\ldots(1)\)
Since, a tangent touches the curve at one point, the root of equation (1) must be equal.
Thus, we get
\(\text { Discriminant }=0\)
\((2 \mathrm{~m}-4)^{2}-4\left(\mathrm{~m}^{2}\right)(1)=0\)
\(\Rightarrow 4 \mathrm{~m}^{2}+16-16 \mathrm{~m}-4 \mathrm{~m}^{2}=0\)
\(\Rightarrow 16-16 \mathrm{~m}=0\)
\(\Rightarrow \mathrm{m}=1\)
Therefore, the required value of \( m \) is 1 .

It is given that the equation of curve is \( 2 y+x^{2}=3 \)
Differentiating w.r.t. \(x\), we get,
\(2 \frac{d y}{d x}+2 x=0\)
\(\Rightarrow \frac{d y}{d x}=-x\)
\(\left.\therefore \frac{d y}{d x}\right]_{(1,1)}=-1\)
The slope of the normal to the given curve at point \( (1,1) \) is
\(\frac{-1}{\left.\frac{d y}{d x}\right]_{(1,1)}}=1\)
Then, the equation of the normal to the curve at \( (1,1) \) is
\(\Rightarrow y-1=1(x-1)\)
\(\Rightarrow y-1=x-1\)
\(\Rightarrow x-y=0\)

It is given that the equation of curve is \( x^{2}=4 y \)
Differentiating w.r.t. \(x \), we get,
\(2 x=4 \frac{d y}{d x}\)
\(\Rightarrow \frac{d y}{d x}=\frac{x}{2}\)
The slope of the normal to the given curve at point \( (\mathrm{h}, \mathrm{k}) \) is
\(\frac{-1}{\left.\frac{d y}{d x}\right]_{(h, k)}}=\frac{-2}{h}\)
Then, the equation of the normal to the curve at \( (\mathrm{h}, \mathrm{k}) \) is
\(\Rightarrow y-\mathrm{k}=\frac{-2}{h}(x-\mathrm{h})\)
Now, it is given that the normal passes through the point \( (1,2) \)
Thus, we get,
\(\Rightarrow 2-\mathrm{k}=\frac{-2}{h}(1-\mathrm{h})\)
\(\Rightarrow \mathrm{k}=2+\frac{2}{h}(1-\mathrm{h}) \ldots (1)\)
Since ( \( h, k \) ) lies on the curve \( x^{2}=4 y \), we have \( h^{2}=4 k \)
\(\Rightarrow \mathrm{k}=\frac{h^{2}}{4}\)
Now putting the value of of \( k \) in (1), we get
\(\frac{h^{3}}{4}=2+\frac{2}{h}(1-\mathrm{h})\)
\(\Rightarrow \frac{h^{3}}{4}=2 \mathrm{~h}+2-2 \mathrm{~h}=2\)
\(\Rightarrow \mathrm{h}^{3}=8\)
\(\Rightarrow \mathrm{h}=2\)
Therefore, the equation of the normal is given as:
\(\Rightarrow y-1=\frac{-2}{2}(x-2)\)
\(\Rightarrow y-1=-(x-2)\)
\(\Rightarrow x+y=3\)

It is given that the equation of the curve is \( 9 y^{2}=x^{3} \)
Differentiating w.r.t. \(x\), we get,
\(9(2 y) \frac{d y}{d x}=3 x^{2}\)
\(\Rightarrow \frac{d y}{d x}=\frac{x^{2}}{6 y}\)
The slope of the normal to the given curve at point \( \left(x_{1}, y_{1}\right) \) is
\(\frac{-1}{\left.\frac{d y}{d x}\right]_{(x 1, y 1)}}=\frac{-6 y_{1}}{x_{1}^{2}}\)
Then, the equation of the normal to the curve at \( \left(x_{1}, y_{1}\right) \) is
\(\Rightarrow y-y_{1}=\frac{-6 y_{1}}{x_{1}^{2}}\left(x-x_{1}\right)\)
\(\Rightarrow x_{1}^{2} y-x_{1}^{2} y_{1}=-6 x y_{1}+6 x_{1} y_{1}\)
\(\Rightarrow 6 x y_{1}+x_{1}^{2} y=6 x_{1} y_{1}+x_{1}^{2} y_{1}\)
\(\Rightarrow \frac{6 x y_{1}}{6 x_{1} y_{1}+x_{1}^{2} y_{1}}+\frac{x_{1}^{2} y}{6 x_{1} y_{1}+x_{1}^{2} y_{1}}=1\)
\(\Rightarrow \frac{x}{\frac{x_{1}\left(6+x_{1}\right)}{6}}+\frac{y}{\frac{y_{1}\left(6+x_{1}\right)}{x_{1}}}=1\)
Now, it is given that the normal makes equal intercepts with the axes.
Thus, we get,
\(\Rightarrow \frac{x_{1}\left(6+x_{1}\right)}{6}=\frac{y_{1}\left(6+x_{1}\right)}{x_{1}}\)
\(\Rightarrow \frac{x_{1}}{6}=\frac{y_{1}}{x_{1}}\)
\(\Rightarrow x_{1}^{2}=6 y_{1} \ldots (1)\)
Since, the point \( \left(x_{1}, y_{1}\right) \) lies on the curve \( 9 y_{1}^{2}=x_{1}^{3} \ldots (2)\)
From (1) and (2), we get
\( 9\left(\frac{x_{1}^{2}}{6}\right)^{2}=x_{1}^{3} \Rightarrow \frac{x_{1}^{4}}{4}=x_{1}^{3} \)
\(\Rightarrow x_{1}=4\)
Now putting the value of \( x_{1} \) in (2), we get
\(9 y_{1}^{2}=4^{3}\)
\(\Rightarrow y_{1}^{2}=\frac{64}{9}\)
\(\Rightarrow y_{1}= \pm \frac{8}{3}\)
Therefore, the required points are \( \left(4, \pm \frac{8}{3}\right) \).