Exercise 3.1 class 9 math solutions || rd sharma class 9 exercise 3.1 || coordinate geometry class 9 extra questions || class 9 maths chapter 3 exercise 3.1 || class 9 maths chapter 3 exercise 3.1 solutions || math class 9 chapter 3 exercise 3.1
Explore detailed, step-by-step solutions to Class 9 Chapter 3 Exercise 3.1 based on Coordinate Geometry. This exercise introduces students to the Cartesian plane, plotting points and understanding coordinates of various geometrical figures. Our carefully explained solutions help students grasp the foundational concepts of coordinate geometry with ease. With clear illustrations and logical steps, these NCERT solutions build spatial understanding and prepare students for more advanced geometry problems in higher classes. For deeper practice and better concept retention, students can also refer to the NCERT Exemplar Class 9 Maths problems.

exercise 3.1 class 9 math solutions || rd sharma class 9 exercise 3.1 || coordinate geometry class 9 extra questions || class 9 maths chapter 3 exercise 3.1 || class 9 maths chapter 3 exercise 3.1 solutions || math class 9 chapter 3 exercise 3.1
Exercise 3.1
1. How will you describe the position of a table lamp on your
study table to another person?
Answer
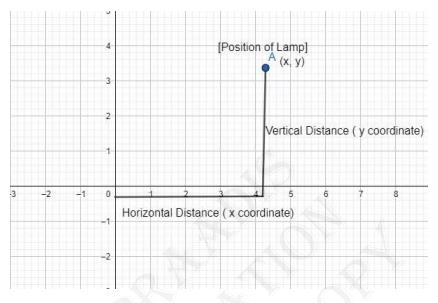
In order to describe the position of a table lamp on the study
table, we will take two lines, perpendicular and horizontal
assuming the table as a plane and taking the perpendicular line as
\(Y\)-axis and horizontal as \(X\) -axis. Now, take one corner of
the table as origin where both \(X\) and \(Y\) axis intersect each
other. Then, the length of table \(Y\) axis and breadth is
\(X\)-axis from the origin.Join the line to the lamp and mark a point. Calculate the distance of this point from both the \(X\) and \(Y\) axis and then write it in the form of coordinates.
Let the distance of the point from \(Y \)-axis is x and from \(X\)-axis is \(y\) then the position of the table lamp in terms of coordinates is ( \( x, y \) )
exercise 3.1 class 9 math solutions || rd sharma class 9 exercise 3.1 || coordinate geometry class 9 extra questions || class 9 maths chapter 3 exercise 3.1 || class 9 maths chapter 3 exercise 3.1 solutions || math class 9 chapter 3 exercise 3.1
Download the Math Ninja App Now2. (Street Plan): A city has two main roads which cross each
other at the centre of the city. These two roads are along the
North-South direction and East-West direction. Rene Descartes
(1596-1650)
All the other streets of the city run parallel to these roads and are 200 m apart. There are about 5 streets in each direction. Using \( 1 \mathrm{~cm}=200 \mathrm{~m} \), draw a model of the city on your notebook Represent the roads/streets by single lines.
There are many cross- streets in your model. A particular cross-street is made by two streets, one running in the North-South direction and another in the East-West direction. Each cross street is referred to in the following manner: If the 2 nd street running in the North - South direction and 5th in the East-West direction meets at some crossing, then we will call this cross-street \( (2,5) \). Using this convention, find:
(i) How many cross - streets can be referred to as \( (4,3) \).
(ii) How many cross - streets can be referred to as \( (3,4) \)
All the other streets of the city run parallel to these roads and are 200 m apart. There are about 5 streets in each direction. Using \( 1 \mathrm{~cm}=200 \mathrm{~m} \), draw a model of the city on your notebook Represent the roads/streets by single lines.
There are many cross- streets in your model. A particular cross-street is made by two streets, one running in the North-South direction and another in the East-West direction. Each cross street is referred to in the following manner: If the 2 nd street running in the North - South direction and 5th in the East-West direction meets at some crossing, then we will call this cross-street \( (2,5) \). Using this convention, find:
(i) How many cross - streets can be referred to as \( (4,3) \).
(ii) How many cross - streets can be referred to as \( (3,4) \)
Answer
As we see from the figure only and only one street can be referred
to as \( (4,3) \) 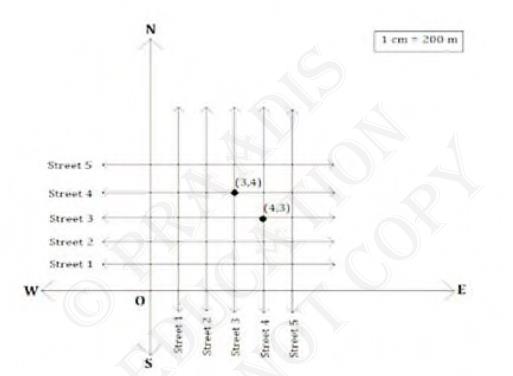
(ii) As we see from the figure only one street can be referred to as \( (3,4) \)

