Class 11 Maths Exercise 6.1 Solutions

The given inequality is \( 24 {x} < 100 \)
\( 24 {x} < 100 \)
\( =\frac{24 x}{24} < \frac{100}{24} \) [Dividing both side by same positive number]
\(=x < \frac{25}{6}\)
(i) It is given that \( 1,2,3 \), and \(4\) are only natural numbers less than \( \frac{25}{6} \)
Thus, when \( x\) is a natural number, the solutions of the given inequality are \( 1,2,3 \), and \(4 \).
Hence, in this case, the solutions set is \( \{1,2,3,4\} \)
(ii) The integers less than are \( \ldots-3,-2,-1,0,1,2,3,4 \)
Thus, when \(x\) is an integer, the solutions of the given inequality are \( \ldots - 3,-2,-1,0,1,2,3,4 \)
Hence, in this case, the solutions set is \( \{-3,-2,-1,0,1,2,3,4\} \)

The given inequality is \( -12 x > 30 \)
\( -12 x > 30 \)
\( =\frac{-12 x}{-12} > \frac{30}{-12} \) [Dividing both sides by same negative number]
\(=x > -\frac{5}{2}\)
(i) There is no natural number less than \( \left(-\frac{5}{2}\right) \)
Thus, when \(x\) is a natural number, there is no solutions of the given inequality.
(ii) The integers less than \( \left(-\frac{5}{2}\right) \) are \( \ldots-5,-4,-3 \).
Thus, when \(x\) is an integer, the solutions of the given inequality are \( \ldots -5,-4,-3 \).
Hence, in this case, the solutions set is \( \{-5,-4,-3\} \)

The given inequality is \( 5 {x}-3 < 7 \)
\(5 x-3 < 7\)
\(=5 x-3+3 < 7+3\)
\(=5 x < 10\)
\(=\frac{5 x}{5} < \frac{10}{5}\)
\(=x < 2\)
(i) The integers less than 2 are \( \ldots-4,-3,-2,-1,0,1 \).
Thus, when \(x\) is an integer, the solutions of the given inequality are \(\ldots -4,-3,-2,-1,0.1 \).
Hence, in this case, the solutions set is \( \{-4,-3,-2,-1,0,1\} \)
(ii) When \(x\) is real number, the solutions of the given inequality are given by \( {x} < 2 \). That is, all real number \(x\) which are less than \(2 \).
Thus, the solutions set of the given inequality is \( x \in(-\infty, 2) \)

The given inequality is \( 3 x+8 > 2 \)
\(=3 x+8-8 > 2-8\)
\(=3 x > -6\)
\(=\frac{3 x}{3} > \frac{-6}{3}\)
\(=x > -2\)
(i) The integers greater than \(-2\) are \( -1,0,1,2, \ldots \)
Thus, when \(x\) is an integer the solutions of the given inequality are \( -1 , 0,1,2, \ldots \)
Hence, in this case, the solutions set is \( \{-1,0,1,2\} \)
(ii) When \(x\) is real number, the solutions of the given are all real numbers, which are greater than \(-2\)
Thus, in this case the solutions set is \( (-2, \infty) \)

It is given in the question that,
\(4 x+3 < 5 x+7\)
Subtracting 7 from both the sides,
\(4 x+3-7 < 5 x+7-7\)
\(4 x-4 < 5 x\)
Subtracting \(4 x\) from both the sides,
\(4 x-4-4 x < 5 x-4 x\)
\(x > -4\)
\( \therefore \) The solutions of the given inequality are defined by all the real numbers greater than \(-4\)
Thus, \( (-4, \infty) \) is the required solution set.

It is given in the question that,
\(4 x+3 < 5 x+7\)
Subtracting 7 from both the sides,
\(4 x+3-7 < 5 x+7-7\)
\(4 x-4 < 5 x\)
Subtracting \(4 x\) from both the sides,
\(4 x-4-4 x < 5 x-4 x\)
\(x > -4\)
\( \therefore \) The solutions of the given inequality are defined by all the real numbers greater than \(-4 \).
Thus, \( (-4, \infty) \) is the required solution set.

It is given in the question that,
\(3(x-1) \leq 2(x-3)\)
\(3 x-3 \leq 2 x-6\)
Adding 3 to both the sides,
\(3 {x}-3+3 \leq 2 {x}-6+3\)
\(3 {x} \leq 2 {x}-3\)
Subtracting \(2 x\) from both the sides,
\(3 x-2 x \leq 2 x-3-2 x\)
\(x \leq-3\)
\( \therefore \) The solutions of the given inequality are defined by all the real numbers less than or equal to \(-3 \).
Thus, \( (-\infty,-3] \) is the required solution set.

It is given in the question that,
\(3(2-x) \geq 2(1-x)\)
\(6-3 x \geq 2-2 x\)
Adding \(2 x\) to both the sides,
\(6-3 x+2 x \geq 2-2 x+2 x\)
\(6-x \geq 2\)
Subtracting 6 from both the sides,
\(6-x-6 \geq 2-6\)
\(-x \geq-4\)
\(x \geq 4\)
\( \therefore \) The solutions of the given inequality are defined by all the real numbers greater than or equal to \(4 \).
Thus, \( [4, \infty) \) is the required solution set.

\({x}+\frac{x}{2}+\frac{x}{3} < 11\)
\(\frac{6 x+3 x+2 x}{6} < 11\)
\(=\frac{11 x}{6} < 11\)
\(=\frac{11 x}{6 \times 11} < \frac{11}{11}\)
\(=\frac{x}{6} < 1\)
\(={x} < 6\)
\( \therefore \) The solutions of the given inequality are defined by all the real numbers less than \(6 \).
Thus, \( (-\infty, 6) \) is the required solution set.

\(\frac{x}{3} > \frac{x}{2}+1\)
\(=\frac{2 x-3 x}{6} > 1\)
\(=-\frac{x}{6} > 1\)
\(=-x > 6\)
\(=x < -6\)
\( \therefore \) The solutions of the given inequality are defined by all the real numbers less than \(-6 \).
Thus, \( (-\infty,-6) \) is the required solution set.

\(\frac{3(x-2)}{5} \leq \frac{5(2-x)}{3}\)
Cross - multiplying the denominators, we get:
\(9(x-2) \leq 25(2-x)\)
\(9 x-18 \leq 50-25 x\)
Adding \(25 x\) both the sides,
\(9 x-18+25 x \leq 50-25 x+25 x\)
\(34 x-18 \leq 50\)
Adding \(25 x\) both the sides,
\(34 x-18+18 \leq 50+18\)
\(34 x \leq 68\)
Dividing both sides by 34,
\(=\frac{34 x}{34} \leq \frac{68}{34}\)
\({x} \leq 2\)
\( \therefore \) The solutions of the given inequality are defined by all the real numbers less than or equal to \(2 \).
Thus, \( (-\infty, 2] \) is the required solution set.

\(\frac{1}{2}\left(\frac{3 x}{5}+4\right) \geq \frac{1}{3}({x}-6)\)
\(=3\left\{\frac{3 x}{5}+4\right\} \geq 2({x}-6)\)
\(=\frac{9 x}{5}+12 \geq 2 {x}-12\)
\(=12+12 \geq 2 {x}-\frac{9 x}{5}\)
\(=24 \geq \frac{10 x-9 x}{5}\)
\(=24 \geq \frac{x}{5}\)
\(=120 \geq {x}\)
\( \therefore \) Thus, all real numbers \(x \), which are less than or equal to \(120\), are the solutions of the given inequality.
Hence, the solutions set of the given inequality is \( (-\infty, 120) \).

It is given in the question that,
\(2(2 x+3)-10 < 6(x-2)\)
\(4 x+6-10 < 6 x-12\)
\(4 x-4 < 6 x-12\)
\(-4+12 < 6 x-4 x\)
\(8 < 2 x\)
\(4 < x\)
\( \therefore \) The solutions of the given inequality are defined by all the real numbers greater than or equal to \(4 \).
Thus, \( [4,-\infty) \) is the required solution set.

We have,
\(37-(3 x+5) \geq 9 x-8(x-3)\)
\(=37-3 x-5 \geq 9 x-8 x+24\)
\(=32-3 x \geq x+24\)
\(=32-24 \geq x+3 x\)
\(=8 \geq 4 x\)
\(=2 \geq x\)
\( \therefore \) All the real numbers of \(x\) which are less than or equal to \(2\) are the solutions of the given inequality
Hence, will be the solution for the given inequality

\(\frac{x}{4} < \frac{(5 x-2)}{3}-\frac{(7 x-3)}{5}\)
\( =\frac{x}{4} < \frac{5(5 x-2)-3(7 x-3)}{15}\)
\(=\frac{x}{4} < \frac{25 x-10-21 x+9}{15}\)
\(=\frac{x}{4} < \frac{4 x-1}{15}\)
\(=15 x < 4(4 x-1)\)
\(=15 x < 16 x-4\)
\(=4 < 16 x-15 x\)
\(=4 < x \)
\( \therefore \) All the real numbers of \(x\) which are greater than \(4\) are the solutions of the given inequality
Hence, will be the solution for the given inequality

\(\frac{(2 x-1)}{3} \geq \frac{(3 x-2)}{4}-\frac{(2-x)}{5}\)
\(=\frac{(2 x-1)}{3} \geq \frac{5(3 x-2)-4(2-x)}{20}\)
\(=\frac{(2 x-1)}{3} \geq \frac{15 x-10-8+4 x}{20}\)
\(=\frac{(2 x-1)}{3} \geq \frac{19 x-18}{20}\)
\(=20(2 x-1) \geq 3(19 x-18)\)
\(=40 x-20 \geq 57 x-54\)
\(=-20+54 \geq 57 x-40 x\)
\(=34 \geq 17 x\)
\(=2 \geq x\)
\( \therefore \) All the real numbers of \( x \) which are less than or equal to \(2\) are the solutions of the given inequality
Hence, will be the solution for the given inequality

We have,
\(3 x-2 < 2 x+1\)
Solving the given inequality, we get:
\(3 x-2 < 2 x+1\)
\(=3 x-2 x < 1+2\)
\(={x} < 3\)
Now, the graphical representation of the solution is as follows:

We have,
Solving the given inequality, we get:
\(5 x-3 \geq 3 x-5\)
\(=5 x-3 x \geq-5+3\)
\(=2 x \geq-2\)
\(=\frac{2 x}{2} \geq \frac{-2}{2}\)
\(=x \geq-1\)
Now, the graphical representation of the solution is as follows:

We have,
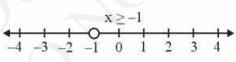
\(3(1-x) < 2(x+4)\)
Solving the given inequality, we get:
\( 3(1-{x}) < 2({x}+4)\)
\(= 3-3 {x} < 2 {x}+8\)
\(= 3-8 < 2 {x}+3 {x}\)
\(= -5 < 5 {x}\)
\(= \frac{-5}{5} < \frac{5 x}{5}\)
\(= -1 < {x}\)
Now, the graphical representation of the solution is as follows:

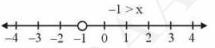
\(\frac{x}{2} \geq \frac{(5 x-2)}{3}-\frac{(7 x-3)}{5}\)
\(=\frac{x}{2} \geq \frac{5(5 x-2)-3(7 x-3)}{15}\)
\(=\frac{x}{2} \geq \frac{25 x-10-21 x+9}{15}\)
\(=\frac{x}{2} \geq \frac{4 x-1}{15}\)
\(=15 {x} \geq 2(4 {x}-1)\)
\(=15 x \geq 8 x-2\)
\(=15 x-8 x \geq 8 x-2-8 x\)
\(=7 x \geq-2\)
\(=x \geq \frac{-2}{7}\)
Now, the graphical representation of the solution is as follows:

Let \(cx\) be marks obtained by Ravi in the third unit test
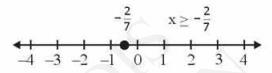
Since the student should have an average of at least 60 marks.
\( \frac{70+75+x}{3} \geq 60 \)
\( =145+x \geq 180\)
\(=x \geq 180-145\)
\(=x \geq 35 \)
Thus, the student must obtain a minimum of 35 marks to have an average of at least 60 marks.

Let \(x\) be the marks obtained by summit in the fifth examination.
In order to receive grade '\( A \)' in the course, she must obtain an averages of 90 marks or more than in five examinations.
Therefore, \( \frac{87+92+94+95}{5} \geq 90 \)
\(=\frac{368+x}{450} \geq 90\)
\(=368+x \geq 450\)
\(=x \geq 450-36\)
\(x\geq 82\)
Thus, summit must obtain greater than or equal to 82 marks in the examination,

Let \( x \) be the smaller of the two consecutive odd positive integer. Than the other integer is \( {x}+2 \).
Since both the integer is smaller than 10.
\(x+2 < 10\)
\(=x < 10-2\)
\(=x < 8 \quad \ldots\text{(1)}\)
Also, the sum of the two integer is more than 11.
\(=x+(x+2) > 11\)
\(=2 x+2 > 11\)
\(=2 x > 11-2\)
\(=2 x > 9\)
\(=x > \frac{9}{2}\)
\(=x > 4.5\quad\ldots\text{(2)}\)
From (1) and (2), we obtain
Since \(x\) is an odd number, \(x\) can take the value, \(5\) and \(7 \).
Thus, the required possible pairs are \( (5,7) \) and \( (7,9) \)

Let \(x\) be the smaller of the two consecutive even positive integers. Than the other integer is \( x+2 \).
Since both the integer are larger than 5
\(x > 5 \quad\ldots\text{(1)}\)
Also, the sum of the two integer is less than 23
\(x+(x+2) < 23\)
\(=2 x+2 < 23\)
\(=2 x < 23-2\)
\(=2 x < 21\)
\(=x < \frac{21}{2}\)
\(=x < 10.5\quad \ldots(2)\)
From (1) and (2), we obtain \( 5 < x < 10.5 \).
Since \(x\) is the even number, \(x\) can take the value, \(6,8\) and \(10 \).
Thus, the required possible pairs are \( (6,8),(8,10) \) and \( (10,12) \)

Let the length of the shortest side of the triangle be \(x\) cm.
Thus, length of the longest side \( =3 x \ {cm} \)
Length of the side \( (3 {x}-2) \ {cm} \)
Since the perimeter of the triangle is at least 61 cm
\(x \ {cm}+3 x \ {cm}+(3 {x}-2) \ {cm} \geq 61 {~cm}\)
\(=7 {x}-2 \geq 61\)
\(=7 {x} \geq 61+2\)
\(=7 {x} \geq 63\)
\(=\frac{7 x}{7} \geq \frac{63}{7}\)
\(=x \geq 9\)
Thus, the minimum length of the shortest side is 9 cm.

Let, the length of the shortest piece be \( x {~cm} \). Then, the length of the second piece and the third piece are \( ({x}+3) \ {cm} \) and \(2 x\) cm respectively.
Since the three lengths are to be cut from a single piece of board of length \( 91 {~cm}, {x} \ {cm}+\{{x}+3\}+2 {x} \ {cm} \leq 91 {~cm} \)
\(=4 x+3 \leq 91\)
\(=4 x \leq 91-3\)
\(=4 x \leq 88\)
\(=\frac{4 x}{4} \leq \frac{88}{4}\)
\(=x \leq 22 \quad\ldots (1)\)
Also, the third piece is at least 5 cm longer than the second piece.
\(=2 x \geq(x+3)+5\)
\(=2 x \geq x+8\)
\(=x \geq 8 \quad\ldots (2) \)
From (1) and (2), we obtain
\(8 \leq x \leq 22\)
Thus, the possible length of the shortest board is greater than or equal to 8 cm but less than or equal to