Coordinate geometry class 9 extra questions || class 9 maths chapter 3 exercise 3.2 solutions || math class 9 chapter 3 exercise 3.2 || class 9 maths chapter 3 exercise 3.2 || rd sharma class 9 exercise 3.2 || exercise 3.2 class 9 math solutions
Explore comprehensive, step-by-step solutions to Class 9 Maths Chapter 3, Exercise 3.2, which focuses on understanding and applying the basics of Coordinate Geometry. This exercise helps students learn how to accurately plot points on the Cartesian plane and identify their coordinates. Each solution is presented with clarity and logical reasoning to strengthen students’ grasp of fundamental geometric concepts. By practicing these problems, learners develop confidence in spatial understanding, which is essential for solving more complex geometry topics in higher grades. For enhanced conceptual clarity and additional practice, students are encouraged to refer to the NCERT Exemplar Class 9 Maths problems.
coordinate geometry class 9 extra questions || class 9 maths chapter 3 exercise 3.2 solutions || math class 9 chapter 3 exercise 3.2 || class 9 maths chapter 3 exercise 3.2 || rd sharma class 9 exercise 3.2 || exercise 3.2 class 9 math solutions
Exercise 3.2
1. Write the answer of each of the following questions:
(i) What is the name of horizontal and the vertical lines drawn
to determine the position of any point in the Cartesian plane?
Answer
\(X \)-axis and \(Y \)-axis are the name of horizontal lines and
vertical lines drawn to determine the position of any point in the
Cartesian plane respectively.
(ii) What is the name of each part of the plane formed by these
two lines?
Answer
The name of each part of the plane formed by these two lines
is:a) \(1^{\text{st}}\) quadrant \( (+x,+y) \)
b) \( 2^{\text {nd }} \) quadrant \( (-x,+y) \)
c) \( 3^{\text {rd }} \) quadrant \( (-x,-y) \)
d) \( 4^{\text {th }} \) quadrant \( (x,-y \) )
coordinate geometry class 9 extra questions || class 9 maths chapter 3 exercise 3.2 solutions || math class 9 chapter 3 exercise 3.2 || class 9 maths chapter 3 exercise 3.2 || rd sharma class 9 exercise 3.2 || exercise 3.2 class 9 math solutions
(iii) Write the name of the point where these two lines
intersect
Answer
origin is termed as the point of intersection of these two lines.
2. See Fig. 3.14, and write the following:
(i)
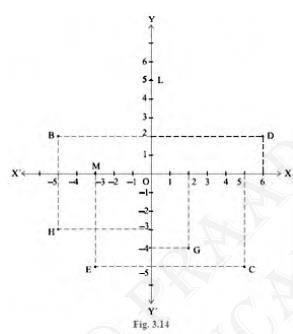
The coordinates of B
The coordinates of B
Answer
For notifying the points shown in the graph. First look at the
horizontal distance of points from Origin.Then look at the vertical distance of point from origin. Distance measured to the right of origin is positive \( x \) axis. And distance measured to the top of origin is positive \(y\) axis. And similarly left and bottom shows negative \(x\) axis and negative \(y\) axis respectively.
The coordinates of B are \( (-5,2) \)
coordinate geometry class 9 extra questions || class 9 maths chapter 3 exercise 3.2 solutions || math class 9 chapter 3 exercise 3.2 || class 9 maths chapter 3 exercise 3.2 || rd sharma class 9 exercise 3.2 || exercise 3.2 class 9 math solutions
(ii)
The coordinates of C
The coordinates of C
Answer
For notifying the points shown in the graph. First look at the
horizontal distance of points from Origin.Then look at the vertical distance of point from origin. Distance measured to the right of origin is positive \( x \) axis. And distance measured to the top of origin is positive \(y\) axis. And similarly left and bottom shows negative \(x\) axis and negative \(y\) axis respectively.
\( (5,-5) \) is the coordinate of C .
(iii)
The point identified by the coordinates \( (-3,-5) \)
The point identified by the coordinates \( (-3,-5) \)
Answer
For notifying the points shown in the graph. First look at the
horizontal distance of points from Origin.Then look at the vertical distance of point from origin. Distance measured to the right of origin is positive \( x \) axis. And distance measured to the top of origin is positive \(y\) axis. And similarly left and bottom shows negative \(x\) axis and negative \(y\) axis respectively.
E is identified by the coordinates \( (-3,-5) \).
(iv)
The point identified by the coordinates \((2, -4)\)
The point identified by the coordinates \((2, -4)\)
Answer
For notifying the points shown in the graph. First look at the
horizontal distance of points from Origin.Then look at the vertical distance of point from origin. Distance measured to the right of origin is positive \( x \) axis. And distance measured to the top of origin is positive \(y\) axis. And similarly left and bottom shows negative \(x\) axis and negative \(y\) axis respectively.
G is the point identified by the coordinates \( (2,-4) \)
(v)
The abscissa of the point D
The abscissa of the point D
Answer
For notifying the points shown in the graph. First look at the
horizontal distance of points from Origin.Then look at the vertical distance of point from origin. Distance measured to the right of origin is positive \( x \) axis. And distance measured to the top of origin is positive \(y\) axis. And similarly left and bottom shows negative \(x\) axis and negative \(y\) axis respectively.
Abscissa means \( x \) coordinate of point D . Hence, abscissa of the point \( D \) is 6
(vi)
The ordinate of the point H
The ordinate of the point H
Answer
For notifying the points shown in the graph. First look at the
horizontal distance of points from Origin.Then look at the vertical distance of point from origin. Distance measured to the right of origin is positive \( x \) axis. And distance measured to the top of origin is positive \(y\) axis. And similarly left and bottom shows negative \(x\) axis and negative \(y\) axis respectively.
Ordinate means y coordinate of point H . Hence, ordinate of point H is \(-3\)
(vii)
The coordinates of the point L
The coordinates of the point L
Answer
For notifying the points shown in the graph. First look at the
horizontal distance of points from Origin.Then look at the vertical distance of point from origin. Distance measured to the right of origin is positive \( x \) axis. And distance measured to the top of origin is positive \(y\) axis. And similarly left and bottom shows negative \(x\) axis and negative \(y\) axis respectively.
The coordinates of the point L is \( (0,5) \)
(viii)
The coordinates of the point M
The coordinates of the point M
Answer
For notifying the points shown in the graph. First look at the
horizontal distance of points from Origin.Then look at the vertical distance of point from origin. Distance measured to the right of origin is positive \( x \) axis. And distance measured to the top of origin is positive \(y\) axis. And similarly left and bottom shows negative \(x\) axis and negative \(y\) axis respectively.
The coordinates of the point M is \( (-3,0) \)
