Class 9 maths chapter 6 exercise 6.2 || rd sharma class 9 Lines and Angles || ncert solutions for class 9 maths chapter 6 exercise 6.2 || ex 6.2 class 9 maths ncert solutions
Explore detailed, step-by-step solutions for Class 9 Maths Chapter 6, Exercise 6.2, centered on the topic of Lines and Angles. This exercise deepens students’ understanding of angle relationships formed when a transversal intersects two lines. It encourages learners to apply previously learned concepts like alternate interior angles, corresponding angles, and consecutive interior angles. Through logical deduction and structured practice, students enhance their ability to identify parallel lines and use angle relationships to solve problems. Exercise 6.2 strengthens analytical thinking and builds a solid base for tackling more complex geometric reasoning in higher classes.

class 9 maths chapter 6 exercise 6.2 || rd sharma class 9 Lines and Angles || ncert solutions for class 9 maths chapter 6 exercise 6.2 || ex 6.2 class 9 maths ncert solutions
Exercise 6.2
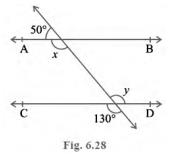
1. In Fig. 6.28, find the values of \(x\) and \(y\) and then show
that \( {AB} \| {CD} \).

Answer
From the figure:\(x+50^{\circ}=180^{\circ} \text { (Linear pair) }\)
\(x=180^{\circ}-50^{\circ}\)
\(x=130^{\circ}\)
And,
\( {y}=130^{\circ} \) (Vertically opposite angles)
Now,
\( x=y=130^{\circ} \) (Alternate interior angles)
Hence,
The theorem says that when the lines are parallel, that the alternate interior angles are equal. And thus the lines must be parallel.
\( {AB} \| {CD} \)
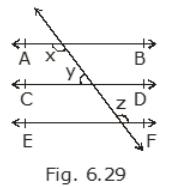
2. In Fig. 6.29, if \( A B\|C D, C D\| E F \) and \( y: z=3: 7
\), Find \( x \).

Answer
It is given in the question that:
\( {AB} \| {CD} \),
Thus, \( \angle {x}+\angle {y}=180^{\circ} \)
(Interior angles on same side of transversal)
(1) Also, \( {AB} \| {CD} \) and \( {CD} \| {EF} \)
Thus, \( {AB} \| {EF} \)
\( \Rightarrow \angle {x}=\angle {z} \) (Alternate interior angles)
(2) From (1) and (2) we can say that,
\(\angle {z}+\angle {y}=180^{\circ}\)
(3) [Angles will be supplementary] It is given that, \( \angle {y}: \angle {z}=3: 7 \)
(4) Let \( \angle {y}=3 \) a and \( \angle {z}=7 \)
a Putting these values in (2)
\(3 {a}+7 {a}=180^{\circ}\)
\(10 {a}=180^{\circ} {a}\)
\(=18^{\circ} \angle {z}=7 {a}\)
\({z}=7 \times 18^{\circ}\)
\(\angle {z}=126^{\circ}\)
As \( \angle {z}=\angle {x} \angle {x}=126^{\circ} \)
class 9 maths chapter 6 exercise 6.2 || rd sharma class 9 Lines and Angles || ncert solutions for class 9 maths chapter 6 exercise 6.2 || ex 6.2 class 9 maths ncert solutions
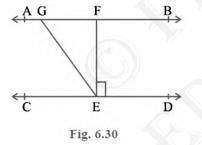
3. In Fig. 6.30, if \( {AB} \| {CD}, {EF} \perp {CD} \) and \(
\angle {GED}=126^{\circ} \), find \( \angle {AGE}, \angle {GEF} \)
and \( \angle {FGE} \).

Answer
It is given in the question that:\( {AB} \| {CD} \)
EF perpendicular CD
\(\angle {GED}=126^{\circ}\)
Now, according to the question,
\( \angle {FED}=90^{\circ} \) (EF perpendicular CD)
Now,
\( \angle {AGE}=\angle {GED} \) (Since, AB parallel CD and GE is transversal, hence alternate interior angles)
Therefore,
\( \angle {AGE}=126^{\circ} \)
And,
\(\angle {GEF}=\angle {GED}-\angle {FED}\)
\(\angle {GEF}=126^{\circ}-90^{\circ}\)
\(\angle {GEF}=36^{\circ}\)
\(\text {Now, }\)
\(\angle {FGE}+\angle {AGE}=180^{\circ} \text { (Linear pair) }\)
\(\angle {FGE}=180^{\circ}-126^{\circ}\)
\(\angle {FGE}=54^{\circ}\)
4. In Fig. 6.31, if \( {PQ} \| {ST}, \angle {PQR}=110^{\circ} \)
and \( \angle {RST}=130^{\circ} \), find \( \angle QRS\).
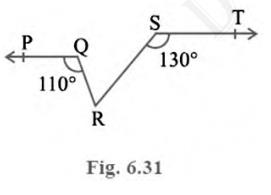

Answer
It is given in the question that:\(PQ\) parallel \(ST\),
\(\angle {PQR}=110^{\circ} \text { and }\)
\(\angle {RST}=130^{\circ}\)
Construction: Draw a line \(XY\) parallel to \(PQ \) and \(ST\)
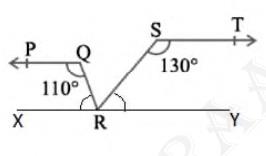
\( \angle {PQR}+\angle {QRX}=180^{\circ} \) (Angles on the same side of transversal)
\( 110^{\circ}+\angle {QRX}=180^{\circ} \)
\( \angle {QRX}=70^{\circ} \)
And,
\( \angle {RST}+\angle {SRY}=180^{\circ} \) (Angles on the same side of transversal)
\( 130^{\circ}+\angle {SRY}=180^{\circ} \)
\( \angle S R Y=50^{\circ} \)
Now,
\( \angle {QRX}+\angle {SRY}+\angle {QRS}=180^{\circ} \) (Angle made on a straight line)
\( 70^{\circ}+50^{\circ}+\angle {QRS}=180^{\circ} \)
\( \angle {QRS}=60^{\circ} \)
5. In Fig. 6.32, if \( {AB} \| {CD}, \angle {APQ}=50^{\circ} \)
and \( \angle {PRD}=127^{\circ} \), find \(x\) and \(y\).


Answer
It is given in the question that:\(AB\) parallel \(CD \),
\( \angle {APQ}=50^{\circ} \) and,
\( \angle {PRD}=127^{\circ} \)
According to question,
\( {x}=50^{\circ} \) (Alternate interior angle)
\( \angle {PRD}+\angle {PRQ}=180^{\circ} \) (Angles on the straight line are supplementary)
\( 127^{\circ}+\angle {PRQ}=180^{\circ} \)
\( \angle {PRQ}=53^{\circ} \)
Now,
In \( \triangle {PQR} \),
\( {x}+{y}+\angle {PRQ}=180^{\circ} \) (Sum of interior angles of a triangle)
\( {y}+50^{\circ}+\angle {PRQ}=180^{\circ} \)
\(y+50^{\circ}+53^{\circ}=180^{\circ}\)
\(y+103^{\circ}=180^{\circ}\)
\(y=77^{\circ}\)
6. In Fig. 6.33, \(PQ\) and \(RS\) are two mirrors placed
parallel to each other. An incident ray \( A B \) strikes the
mirror \( P Q \) at \( B \), the reflected ray moves along the
path \(BC\) and strikes the mirror \(RS\) at \(C\) and again
reflects back along \( C D \). Prove that \( A B \| C D \).
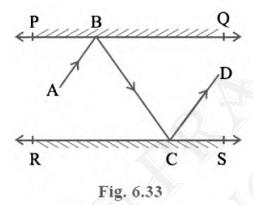

Answer
Given: Two mirrors are parallel to each other, \( P Q \| R S \)To Prove: \( {AB} \| {CD} \)
Proof:
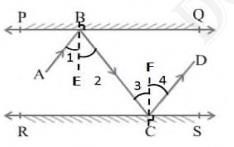
Take two perpendiculars BE and CF, As the mirrors are parallel to each other their perpendiculars will also be parallel thus \( {BE} \| {CF} \)
According to laws of reflection, we know that:
Angle of incidence \( = \) Angle of reflection
\( \angle 1=\angle 2 \) and,
\( \angle 3=\angle 4 \) (i)
And,
\( \angle 2=\angle 3 \) (Alternate interior angles, since BE, is parallel to CF and a transversal line BC cuts them at B and C respectively) (ii)
We need to prove that \( \angle {ABC}=\angle {DCB} \angle {ABC}=\angle 1+\angle 2 \) and \( \angle {DCB}= \) \( \angle 3+\angle 4 \)
From (i) and (ii), we get
\(\angle 1+\angle 2=\angle 3+\angle 4\)
\(\Rightarrow \angle {ABC}=\angle {DCB}\)
\( \Rightarrow {AB} \) parallel CD (Alternate interior angles)
Hence, Proved.

