Class 9 ncert exercise 7.2 || ncert class 9 exercise 7.2 || maths chapter 7 class 9 exercise 7.2 || rd sharma class 9 triangle || chapter 7 exercise 7.2 class 9 || class 9 maths chapter 7 exercise 7.2 solutions || exercise 7.2 maths class 9 || exercise 7.2 class 9 maths || chapter 7 maths class 9 exercise 7.2
Explore clear, step-by-step solutions for Class 9 Maths Chapter 7, Exercise 7.2, which focuses on the concept of congruence of triangles. This exercise helps students understand how to determine when two triangles are congruent using different rules such as SAS (Side-Angle-Side), ASA (Angle-Side-Angle), and SSS (Side-Side-Side). Through solving these problems, learners begin to recognize congruent parts of triangles and apply these congruence rules to prove geometric relationships. Exercise 7.2 not only strengthens students’ reasoning and proof skills but also sets a strong foundation for solving more complex geometry problems in higher classes involving triangle properties and construction.

class 9 ncert exercise 7.2 || ncert class 9 exercise 7.2 || maths chapter 7 class 9 exercise 7.2 || rd sharma class 9 triangle || chapter 7 exercise 7.2 class 9 || class 9 maths chapter 7 exercise 7.2 solutions || exercise 7.2 maths class 9 || exercise 7.2 class 9 maths || chapter 7 maths class 9 exercise 7.2
Exercise 7.2
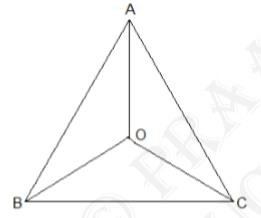
1. In an isosceles triangle \( A B C \), with \( A B=A C \), the
bisectors of \( B \) and \( C \) intersect each other at \( O \).
Join \( A \) to \( O \). Show that:
(i) \( \mathrm{OB}=\mathrm{OC} \)
(ii) \(AO\) bisects \(A\)
(i) \( \mathrm{OB}=\mathrm{OC} \)
(ii) \(AO\) bisects \(A\)

Answer
Given:\( \mathrm{AB}=\mathrm{AC} \) and
the bisectors of \(B\) and \(C\) intersect each other at \(O\)
(i) Since \( \mathrm{ABC}\) is an isosceles with \( \mathrm{AB}=\mathrm{AC} \), \( B=C \)
\( \frac{ 1 }{ 2 } B=\frac{ 1 }{ 2 } C \)
\( \Rightarrow \mathrm{OBC}=\mathrm{OCB} \) (Angle bisectors)
\( \therefore \mathrm{OB}=\mathrm{OC} \) (Side opposite to the equal angles are equal.)
(ii) In \( \triangle \mathrm{AOB} \) and \( \triangle \mathrm{AOC} \),
\( \mathrm{AB}=\mathrm{AC} \) (Given in the question)
\( \mathrm{AO}=\mathrm{AO} \) (Common arm)
\( \mathrm{OB}=\mathrm{OC} \) (As Proved Already)
So, \( \triangle \mathrm{AOB} \Delta \mathrm{AOC} \) by SSS congruence condition.
\( \mathrm{BAO}=\mathrm{CAO}( \) by CPCT)
Thus, \(AO\) bisects \(A\).
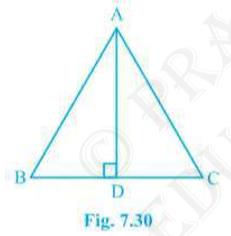
2. In \( \triangle \mathrm{ABC}, \mathrm{AD} \) is the
perpendicular bisector of \( \mathrm{BC}\) (see Fig. 7.30). Show
that \( \triangle \mathrm{ABC} \) is an isosceles triangle in
which \( \mathrm{AB}=\mathrm{AC} \).

Answer
It is given that \( \mathrm{AD}\) is the perpendicular bisector of
\( \mathrm{BC}\)To prove:
\(\mathrm{AB}=\mathrm{AC}\)
Proof:
In \( \triangle \mathrm{ADB} \) and \( \triangle \mathrm{ADC} \),
\( \mathrm{AD}=\mathrm{AD} \) (It is the Common arm)
\( \mathrm{ADB}=\mathrm{ADC} \)
\( \mathrm{BD}=\mathrm{CD} \) (Since AD is the perpendicular bisector)
So, \( \triangle \mathrm{ADB} \triangle \mathrm{ADC} \) by SAS congruency criterion.
Thus,
\( \mathrm{AB}=\mathrm{AC}\) (by CPCT \( ) \)
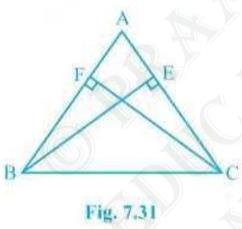
3. ABC is an isosceles triangle in which altitudes BE and CF are
drawn to equal sides AC and AB respectively (see Fig. 7.31). Show
that these altitudes are equal.

Answer
Given:(i) \( \mathrm{BE}\) and \( \mathrm{CF}\) are altitudes.
(ii) \( \mathrm{AC}=\mathrm{AB} \)
To prove:
\(\mathrm{BE}=\mathrm{CF}\)
Proof:
Triangles \( \triangle \mathrm{AEB} \) and \( \triangle \mathrm{AFC} \) are similar by AAS congruency since
\( \mathrm{A}=\mathrm{A} \) (It is the common arm)
\( \mathrm{AEB}=\mathrm{AFC} \) (They are right angles)
\( \mathrm{AB}=\mathrm{AC} \) (Given in the question)
\( \therefore \triangle \mathrm{AEB} \triangle \mathrm{AFC} \) and so, \( \mathrm{BE}=\mathrm{CF}( \) by CPCT\( ) \).
class 9 ncert exercise 7.2 || ncert class 9 exercise 7.2 || maths chapter 7 class 9 exercise 7.2 || rd sharma class 9 triangle || chapter 7 exercise 7.2 class 9 || class 9 maths chapter 7 exercise 7.2 solutions || exercise 7.2 maths class 9 || exercise 7.2 class 9 maths || chapter 7 maths class 9 exercise 7.2
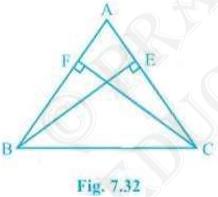
4. \( \mathrm{ABC}\) is a triangle in which altitudes \(
\mathrm{BE}\) and \( \mathrm{CF}\) to sides \( \mathrm{AC}\) and
\( \mathrm{AB}\) are equal (see Fig. 7.32). Show that
(i) \( \triangle \mathrm{ABE} \triangle \mathrm{ACF} \)
(ii) \( \mathrm{AB}=\mathrm{AC} \), i.e., \( \mathrm{ABC}\) is an isosceles triangle.
(i) \( \triangle \mathrm{ABE} \triangle \mathrm{ACF} \)
(ii) \( \mathrm{AB}=\mathrm{AC} \), i.e., \( \mathrm{ABC}\) is an isosceles triangle.

Answer
It is given that \( \mathrm{BE}=\mathrm{CF} \)(i) In \( \triangle \mathrm{ABE} \) and \( \triangle \mathrm{ACF} \),
\( \mathrm{A}=\mathrm{A} \) (It is the common angle)
\( \mathrm{AEB}=\mathrm{AFC} \) (They are right angles)
\( \mathrm{BE}=\mathrm{CF} \) (Given in the question)
\( \therefore \triangle \mathrm{ABE} \triangle \mathrm{ACF} \) by AAS congruency condition.
(ii) \( \mathrm{AB}=\mathrm{AC} \) by CPCT and so, \( \mathrm{ABC}\) is an isosceles triangle.
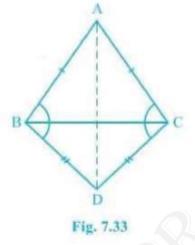
5. \( \mathrm{ABC}\) and \( \mathrm{DBC}\) are two isosceles
triangles on the same base \( \mathrm{BC}\) (see Fig. 7.33). Show
that \( \mathrm{ABD}= \mathrm{ACD}\).

Answer
In the question, it is given that \( \mathrm{ABC}\) and \(
\mathrm{DBC}\) are two isosceles triangles. We will have to show
that \( \mathrm{ABD}=\mathrm{ACD} \)Proof:
Triangles \( \triangle \mathrm{ABD} \) and \( \triangle \mathrm{ACD} \) are similar by SSS congruency since
\( \mathrm{AD}=\mathrm{AD} \) (It is the common arm)
\( \mathrm{AB}=\mathrm{AC} \) (Since \( \mathrm{ABC}\) is an isosceles triangle)
\( \mathrm{BD}=\mathrm{CD} \) (Since \( \mathrm{BCD}\) is an isosceles triangle)
So, \( \triangle \mathrm{ABD} \triangle \mathrm{ACD} \).
\( \therefore \mathrm{ABD}=\mathrm{ACD} \) by CPCT .
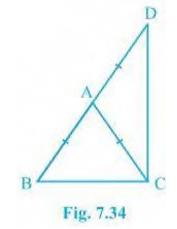
6. \( \triangle \mathrm{ABC} \) is an isosceles triangle in which
\( \mathrm{AB}=\mathrm{AC} \). Side \( \mathrm{BA}\) is produced
to \( \mathrm{D}\) such that \( \mathrm{AD}=\mathrm{AB} \) (see
Fig. 7.34). Show that \( \mathrm{BCD}\) is a right angle.

Answer
It is given that \(\mathrm{AB}= \mathrm{AC}\) and
\(\mathrm{AD}=\mathrm{AB}\)We will have to now prove \( \mathrm{BCD}\) is a right angle.
Proof:
Consider \( \triangle \mathrm{ABC} \),
\( \mathrm{AB}=\mathrm{AC} \) (It is given in the question)
Also, \( \mathrm{ACB}=\mathrm{ABC} \) (They are angles opposite to the equal sides and so, they are equal)
Now, consider \( \triangle \mathrm{ACD} \),
\(\mathrm{AD}=\mathrm{AB}\)
Also, \( \mathrm{ADC}=\mathrm{ACD} \) (They are angles opposite to the equal sides and so, they are equal)
Now,
In \( \triangle \mathrm{ABC} \),
\(\mathrm{CAB}+\mathrm{ACB}+\mathrm{ABC}=180^{\circ}\)
So, \( \mathrm{CAB}+2 \mathrm{ACB}=180^{\circ} \)
\(\Rightarrow \mathrm{CAB}=180^{\circ}-2 \mathrm{ACB}\ldots\text { (i) }\)
Similarly, in \( \triangle \mathrm{ADC} \),
\(\mathrm{CAD}=180^{\circ}-2 \mathrm{ACD}\ldots\text { (ii) }\)
also,
\( \mathrm{CAB}+\mathrm{CAD}=180^{\circ}(\mathrm{BD} \) is a straight line. \( ) \)
Adding (i) and (ii) we get,
\(\mathrm{CAB}+\mathrm{CAD}=180^{\circ}-2 \mathrm{ACB}+180^{\circ}-2 \mathrm{ACD}\)
\(\Rightarrow 180^{\circ}=360^{\circ}-2 \mathrm{ACB}-2 \mathrm{ACD}\)
\(\Rightarrow 2(\mathrm{ACB}+\mathrm{ACD})=180^{\circ}\)
\(\Rightarrow \mathrm{BCD}=90^{\circ}\)
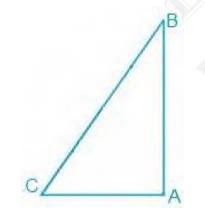
7. ABC is a right-angled triangle in which \(
\mathrm{A}=90^{\circ} \) and \( \mathrm{AB}=\mathrm{AC} \). Find
\( B \) and \( C \).
Answer
In the question, it is given that
\( \mathrm{A}=90^{\circ} \) and \( \mathrm{AB}=\mathrm{AC} \)
\( \mathrm{AB}=\mathrm{AC} \)
\( \Rightarrow \mathrm{B}=\mathrm{C} \) (They are angles opposite to the equal sides and so, they are equal)
Now,
\( \mathrm{A}+\mathrm{B}+\mathrm{C}=180^{\circ} \) (Since the sum of the interior angles of the triangle)
\(\therefore 90^{\circ}+2 \mathrm{B}=180^{\circ}\)
\(\Rightarrow 2 \mathrm{B}=90^{\circ}\)
\(\Rightarrow \mathrm{B}=45^{\circ}\)
So, \( B=C=45^{\circ} \)
8. Show that the angles of an equilateral triangle are \(
60^{\circ} \) each.
Answer
Let ABC be an equilateral triangle as shown below: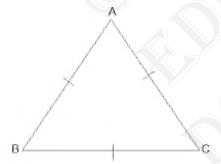
Here, \( \mathrm{BC}=\mathrm{AC}=\mathrm{AB} \quad\) (Since the length of all sides is same)
\( \Rightarrow \mathrm{A}=\mathrm{B}=\mathrm{C} \quad\) (Sides opposite to the equal angles are equal.)
Also, we know that
\(\mathrm{A}+\mathrm{B}+\mathrm{C}=180^{\circ}\)
\(\Rightarrow 3 \mathrm{A}=180^{\circ}\)
\(\Rightarrow \mathrm{A}=60^{\circ}\)
\(\therefore \mathrm{A}=\mathrm{B}=\mathrm{C}=60^{\circ}\)
So, the angles of an equilateral triangle are always \( 60^{\circ} \) each.

