Exercise 8.1 class 9 solutions || exercise 8.1 class 9 || quadrilaterals class 9 exercise 8.1 || class 9 quadrilaterals exercise 8.1 || class 9 maths chapter 8 exercise 8.1 || exercise 8.1 class 9 maths || ncert solutions for class 9 chapter quadrilaterals exercise 8.1 || class 9 exercise 8.1
Explore clear, step-by-step solutions for Class 9 Maths Chapter 8, Exercise 8.1, which introduces students to the fundamental properties and classification of quadrilaterals. This exercise helps learners build a strong understanding of the relationships between sides, angles, and diagonals in various types of quadrilaterals, such as parallelograms, rectangles, rhombuses and squares. Through logically structured questions, students learn to apply previously learned theorems—especially those related to triangle congruence—to prove properties of quadrilaterals. Solving these problems not only enhances their reasoning and analytical skills but also improves their ability to construct geometrical proofs effectively.

exercise 8.1 class 9 solutions || exercise 8.1 class 9 || quadrilaterals class 9 exercise 8.1 || class 9 quadrilaterals exercise 8.1 || class 9 maths chapter 8 exercise 8.1 || exercise 8.1 class 9 maths || ncert solutions for class 9 chapter quadrilaterals exercise 8.1 || class 9 exercise 8.1
Exercise 8.1
1. The angles of quadrilateral are in the ratio 3: 5: 9: 13. Find
all the angles of the quadrilateral.
Answer
Let the common ratio between the angles be \( x \). Therefore, the
angles will be \( 3 x, 5 x, 9 x \), and \(13 x\) respectivelyAs the sum of all interior angles of a quadrilateral is \( 360^{\circ} \).
\(3 x+5 x+9 x+13 x=360^{\circ}\)
\(30 x=360^{\circ}\)
\(x=12^{\circ}\)
Hence, the angles are
\(3 x=3 \times 12=36^{\circ}\)
\(5 x=5 \times 12=60^{\circ}\)
\(9 x=9 \times 12=108^{\circ}\)
\(13 x=13 \times 12=156^{\circ}\)
2. If the diagonals of a parallelogram are equal, then show that
it is a rectangle.
Answer
Let ABCD be a parallelogram. To show that ABCD is a rectangle,We have to prove that: One of its interior angles is \( 90^{\circ} \).
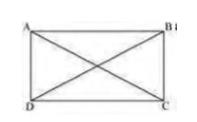
In \( \triangle \mathrm{ABC} \) and \( \triangle \mathrm{DCB} \),
\( \mathrm{AB}=\mathrm{DC} \) (Opposite sides of a parallelogram are equal)
\( \mathrm{BC}=\mathrm{BC}( \) Common \( ) \)
\( \mathrm{AC}=\mathrm{DB} \) (Given that the diagonals are equal)
\( \Delta \mathrm{ABC} \cong \triangle \mathrm{DCB}(\mathrm{By} \) \(SSS\) Congruence rule)
\( \angle \mathrm{ABC}=\angle \mathrm{DCB} \)
It is known that the sum of the measures of angles on the same side of transversal is \( 180^{\circ} \)
\(\angle \mathrm{ABC}+\angle \mathrm{DCB}=180^{\circ}(\mathrm{AB} \| \mathrm{CD})\)
\(\angle \mathrm{ABC}+\angle \mathrm{ABC}=180^{\circ}\)
\(\angle \mathrm{ABC}=90^{\circ}\)
Since \( A B C D \) is a parallelogram and one of its interior angles is \( 90^{\circ} \), ABCD is a rectangle.
3. Show that if the diagonals of a quadrilateral bisect each
other at right angles, then it is a rhombus.
Answer
To Prove: If diagonals of a quadrilateral bisect at \( 90^{\circ}
\), it is a rhombus.Figure:
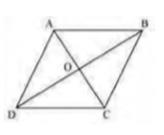
Definition of Rhombus: A parallelogram whose all sides are equal.
Given: Let ABCD be a quadrilateral whose diagonals bisect at \( 90^{\circ}\)
In \( \triangle \mathrm{AOD} \) and \( \triangle \mathrm{COD} \),
\( \mathrm{OA}=\mathrm{OC} \) (Diagonals bisect each other)
\( \angle \mathrm{AOD}=\angle \mathrm{COD} \) (Given)
\( \mathrm{OD}=\mathrm{OD}( \) Common)
\( \triangle \mathrm{AOD} \cong \triangle \mathrm{COD}(\mathrm{By} \) \(SAS\) congruence rule)
\( \mathrm{AD}=\mathrm{CD} \ldots(1)\)
Similarly,
\( \mathrm{AD}=\mathrm{AB} \) and \( \mathrm{CD}=\mathrm{BC} \ldots(2)\)
From equations (1) and (2),
\(\mathrm{AB}=\mathrm{BC}=\mathrm{CD}=\mathrm{AD}\)
Since opposite sides of quadrilateral ABCD are equal, it can be said that \( A B C D \) is a parallelogram. Since all sides of a parallelogram \( A B C D \) are equal, it can be said that
ABCD is a rhombus
Hence, Proved.
4. Show that the diagonals of a square are equal and bisect each
other at right angles.
Answer
Let ABCD be a square. Let the diagonals AC and BD intersect each
other at a point \( O \).To prove that the diagonals of a square are equal and bisect each other at right angles,
We have to prove: \( \mathrm{AC}=\mathrm{BD}, \mathrm{OA}=\mathrm{OC}, \mathrm{OB}=\mathrm{OD} \) and \( \angle \mathrm{AOB}=90^{\circ} \)
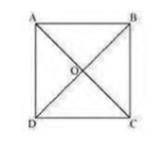
In \( \triangle \mathrm{ABC} \) and \( \triangle \mathrm{DCB} \),
\( \mathrm{AB}=\mathrm{DC} \) (Sides of a square are equal to each other)
\( \angle \mathrm{ABC}=\angle \mathrm{DCB} \) (angles of square are \( 90^{\circ} \) )
\( \mathrm{BC}=\mathrm{CB}( \) Common side \( ) \)
\( \Delta \mathrm{ABC} \ \Delta \mathrm{DCB} \) (By \(SAS\) congruency)
\( \mathrm{AC}=\mathrm{DB}(\mathrm{By} \mathrm{CPCT}) \)
Hence, the diagonals of a square are equal in length.
In \( \triangle \mathrm{AOB} \) and \( \triangle \mathrm{COD} \),
\( \angle \mathrm{AOB}=\angle \mathrm{COD} \) (Vertically opposite angles)
\( \angle \mathrm{ABO}=\angle \mathrm{CDO} \) (Alternate interior angles)
\( \mathrm{AB}=\mathrm{CD}( \) Sides of a square are always equal \( ) \)
\( \triangle \mathrm{AOB} \ \triangle \mathrm{COD} \) (By \(AAS\) congruence rule)
\( \mathrm{AO}=\mathrm{CO} \) and
\( \mathrm{OB}=\mathrm{OD}(\mathrm{By} \mathrm{CPCT}) \)
Hence, the diagonals of a square bisect each other
In \( \triangle \mathrm{AOB} \) and \( \triangle \mathrm{COB} \),
As we had proved that diagonals bisect each other, therefore,
\( \mathrm{AO}=\mathrm{CO} \)
\( \mathrm{AB}=\mathrm{CB} \) (Sides of a square are equal)
\( \mathrm{BO}=\mathrm{BO} \) (Common)
\( \Delta \mathrm{AOB} \cong \Delta \mathrm{COB} \) (By \(SSS\) congruency)
\( \angle \mathrm{AOB}=\angle \mathrm{COB}(\mathrm{By} \) CPCT \( ) \)
However,
\(\angle \mathrm{AOB}+\angle \mathrm{COB}=180^{\circ}(\text { Linear pair })\)
\(2 \angle \mathrm{AOB}=180^{\circ}\)
\(\angle \mathrm{AOB}=90^{\circ}\)
Hence, the diagonals of a square bisect each other at right angles.
5. Show that if the diagonals of a quadrilateral are equal and
bisect each other at right angles, then it is a square.
Answer
Let us consider a quadrilateral ABCD in which the diagonals AC and
BD intersect each other at O . It is given that the diagonals of ABCD are equal and bisect each other at right angles.
Therefore, \( \mathrm{AC}=\mathrm{BD}, \mathrm{OA}=\mathrm{OC}, \mathrm{OB}=\mathrm{OD} \), and
\( \angle \mathrm{AOB}=\angle \mathrm{BOC}=\angle \mathrm{COD}=\angle \mathrm{AOD}=90^{\circ} \)
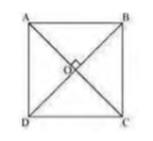
To prove: \( A B C D \) is a square,
Proof:
we have to prove that \( A B C D \) is a parallelogram with all of its sides equal and one of the interior angle is right angle.
or,
\( \mathrm{AB}=\mathrm{BC}=\mathrm{CD}=\mathrm{AD} \), and one of its interior angles is 900
In \( \triangle \mathrm{AOB} \) and \( \triangle \mathrm{COD} \),
\( \mathrm{AO}=\mathrm{CO} \) (Diagonals bisect each other)
\( \mathrm{OB}=\mathrm{OD} \) (Diagonals bisect each other)
\( \angle \mathrm{AOB}=\angle \mathrm{COD} \) (Vertically opposite angles)
(\(SAS\)) Definition: Triangles are congruent if any pair of corresponding sides and their included angles are equal in both triangles.
\( \triangle \mathrm{AOB} \Delta \mathrm{COD} \) (SAS congruence rule)
\( \mathrm{AB}=\mathrm{CD}(\mathrm{By} \mathrm{CPCT}) \ldots(1)\)
And,
\( \angle \mathrm{OAB}=\angle \mathrm{OCD}( \) By CPCT \( ) \)
However, these are alternate interior angles for line \( A B \) and \( C D \) and alternate interior angles are equal to each other only when the two lines are parallel
\( \mathrm{AB} \| \mathrm{CD} \ldots(2)\)
From equations (1) and (2), we obtain ABCD is a parallelogram
(Theorem: Quadrilateral with any of opposite sides equal and parallel is a parallelogram.)
In \( \triangle \mathrm{AOD} \) and \( \triangle \mathrm{COD} \),
\( \mathrm{AO}=\mathrm{CO} \) (Diagonals bisect each other)
\( \angle \mathrm{AOD}=\angle \mathrm{COD} \) (Given that each is 900 )
\( \mathrm{OD}=\mathrm{OD}( \) Common \( ) \)
\( \triangle \mathrm{AOD} \cong \triangle \mathrm{COD} \) (\(SAS\) congruence rule)
\( \mathrm{AD}=\mathrm{DC}\ldots(3) \)
However,
\( \mathrm{AD}=\mathrm{BC} \) and
\( \mathrm{AB}=\mathrm{CD} \) (Opposite sides of parallelogram ABCD\( ) \)
\( \mathrm{AB}=\mathrm{BC}=\mathrm{CD}=\mathrm{DA} \)
Therefore, all the sides of quadrilateral ABCD are equal to each other.
In \( \triangle \mathrm{ADC} \) and \( \triangle \mathrm{BCD} \),
\(\mathrm{AD}=\mathrm{BC}(\text { Already proved })\)
\(\mathrm{AC}=\mathrm{BD}(\text { Given })\)
\(\mathrm{DC}=\mathrm{CD}(\text { Common })\)
\(\Delta \mathrm{ADC} \cong \triangle \mathrm{BCD}(\text {SSS Congruence rule })\)
\(\angle \mathrm{ADC}=\angle \mathrm{BCD}(\text { By CPCT })\)
However,
\(\angle \mathrm{ADC}+\angle \mathrm{BCD}=180^{\circ}(\text { Co-interior angles })\)
\(\angle \mathrm{ADC}+\angle \mathrm{ADC}=180^{\circ}\)
\(2 \angle \mathrm{ADC}=180^{\circ}\)
\( \angle \mathrm{ADC}=90^{\circ} \) One of the interior angles of quadrilateral ABCD is a right angle.
Thus, we have obtained that ABCD is a parallelogram, \( \mathrm{AB}=\mathrm{BC}=\mathrm{CD}= AD\) and one of its interior angles is \( 90^{\circ} \)
Therefore, ABCD is a square.
exercise 8.1 class 9 solutions || exercise 8.1 class 9 || quadrilaterals class 9 exercise 8.1 || class 9 quadrilaterals exercise 8.1 || class 9 maths chapter 8 exercise 8.1 || exercise 8.1 class 9 maths || ncert solutions for class 9 chapter quadrilaterals exercise 8.1 || class 9 exercise 8.1
6. Diagonal AC of a parallelogram ABCD bisects \( \angle
\mathrm{A} \) (see Fig. 8.19). Show that
(i) It bisects \( \angle \mathrm{C} \) also,
(ii) ABCD is a rhombus.
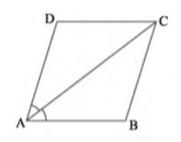
(i) It bisects \( \angle \mathrm{C} \) also,
(ii) ABCD is a rhombus.

Answer
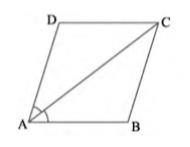
(i) ABCD is a parallelogram.
\( \angle \mathrm{DAC}=\angle \mathrm{BCA} \) (Alternate interior angles) \( \ldots(1)\)
And,
\( \angle \mathrm{BAC}=\angle \mathrm{DCA} \) (Alternate interior angles) \(\ldots(2)\)
However, it is given that AC bisects A
\(\angle \mathrm{DAC}=\angle \mathrm{BAC} \ldots(3)\)
From equations (1), (2), and (3), we obtain
\(\angle \mathrm{DAC}=\angle \mathrm{BCA}=\angle \mathrm{BAC}=\angle \mathrm{DCA} \ldots(4)\)
\(\angle \mathrm{DCA}=\angle \mathrm{BCA}\)
Hence, AC bisects C
(ii) From equation (4), we obtain
\( \angle \mathrm{DAC}=\angle \mathrm{DCA} \)
\( \mathrm{DA}=\mathrm{DC} \) (Side opposite to equal angles are equal)
However,
\( \mathrm{DA}=\mathrm{BC} \) and \( \mathrm{AB}=\mathrm{CD} \) (Opposite sides of a parallelogram)
\( \mathrm{AB}=\mathrm{BC}=\mathrm{CD}=\mathrm{DA} \)
Hence, ABCD is a rhombus
7. ABCD is a rhombus. Show that diagonal AC bisects \( \angle
\mathrm{A} \) as well as \( \angle \mathrm{C} \) and diagonal BD
bisects \( \angle \mathrm{B} \) as well as \( \angle \mathrm{D}
\).
Answer
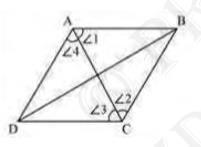
To Prove: \( \angle 1=\angle 4, \angle 2=\angle 3 \)
Proof:
In \( \triangle \mathrm{ABC} \),
\( \mathrm{BC}=\mathrm{AB} \quad \) (Sides of a rhombus are equal to each other)
\( \angle 1=\angle 2 \quad \) (Angles opposite to equal sides of a triangle are equal)
However,
\( \angle 1=\angle 3 \) (Alternate interior angles for parallel lines AB and CD )
\(\angle 2=\angle 3\)
Therefore, AC bisects \( \angle \mathrm{C} \)
Also,
\( \angle 2=\angle 4 \quad \) (Alternate interior angles for \( \| \) lines BC and DA)
\(\angle 1=\angle 4\)
Therefore,
AC bisects \( \angle \mathrm{A} \)
Hence, Proved.
Similarly, it can be proved that BD bisects B and D as well.
8. ABCD is a rectangle in which diagonal AC bisects \( \angle
\mathrm{A} \) as well as \( \angle \mathrm{C} \) Show that:
(i) ABCD is a square
(ii) Diagonal BD bisects \( \angle \mathrm{B} \) as well as \( \angle \mathrm{D} \)
(i) ABCD is a square
(ii) Diagonal BD bisects \( \angle \mathrm{B} \) as well as \( \angle \mathrm{D} \)

Answer
Given: \( A B C D \) is a rectangle,\(\angle \mathrm{A}=\angle \mathrm{C} \)
To Prove: \( A B C D \) is a square Proof:
\( \angle \mathrm{DAC}=\angle \mathrm{DCA}(\mathrm{AC} \) bisects A and C\( ) \)
\( \mathrm{CD}=\mathrm{DA} \) (Sides opposite to equal angles are also equal)
However,
\( \mathrm{DA}=\mathrm{BC} \) and \( \mathrm{AB}=\mathrm{CD} \) (Opposite sides of a rectangle are equal)
\(\mathrm{AB}=\mathrm{BC}=\mathrm{CD}=\mathrm{DA}\)
\( A B C D \) is a rectangle and all of its sides are equal.
Hence, ABCD is a square
Hence, Proved.
(ii) Let us join BD
In \( \triangle \mathrm{BCD} \),
\( \mathrm{BC}=\mathrm{CD} \) (Sides of a square are equal to each other)
\( \angle \mathrm{CDB}=\angle \mathrm{CBD} \) (Angles opposite to equal sides are equal)
However,
\( \angle \mathrm{CDB}=\angle \mathrm{ABD} \) (Alternate interior angles for \( \mathrm{AB} \| \mathrm{CD} \) )
\( \angle \mathrm{CBD}=\angle \mathrm{ABD} \)
BD bisects B
Also,
\( \angle \mathrm{CBD}=\angle \mathrm{ADB} \) (Alternate interior angles for \( \mathrm{BC} \| \mathrm{AD} \) )
\( \angle \mathrm{CDB}=\angle \mathrm{ABD} \)
BD bisects D .
9. In parallelogram \( A B C D \), two points \( P \) and \( Q \)
are taken on diagonal BD such that \( \mathrm{DP}=\mathrm{BQ} \)
(see Fig. 8.20). Show that:
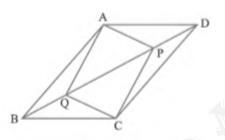
(i) \( \Delta \mathrm{APD} \cong \Delta \mathrm{CQB} \)
(ii) \( \mathrm{AP}=\mathrm{CQ} \)
(iii) \( \Delta \mathrm{AQB} \cong \triangle \mathrm{CPD} \)
(iv) \( \mathrm{AQ}=\mathrm{CP} \)
(v) \(APCQ\) is a parallelogram

(i) \( \Delta \mathrm{APD} \cong \Delta \mathrm{CQB} \)
(ii) \( \mathrm{AP}=\mathrm{CQ} \)
(iii) \( \Delta \mathrm{AQB} \cong \triangle \mathrm{CPD} \)
(iv) \( \mathrm{AQ}=\mathrm{CP} \)
(v) \(APCQ\) is a parallelogram
Answer
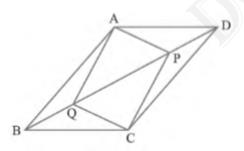
(i) In \( \triangle \mathrm{APD} \) and \( \triangle \mathrm{CQB} \),
\( \angle \mathrm{ADP}=\angle \mathrm{CBQ} \) (Alternate interior angles for \( \mathrm{BC} \| \mathrm{AD} \) )
\( \mathrm{AD}=\mathrm{CB} \) (Opposite sides of parallelogram ABCD\( ) \)
\( \mathrm{DP}=\mathrm{BQ} \) (Given)
Two sides and included angle (SAS) Definition: Triangles are congruent if any pair of corresponding sides and their included angles are equal in both triangles.
\( \triangle \mathrm{APD} \triangle \mathrm{CQB} \) (Using SAS congruence rule)
(ii) As we had observed that,
\(\triangle \mathrm{APD} \cong \Delta \mathrm{CQB}\)
\(\mathrm{AP}=\mathrm{CQ}(\mathrm{CPCT})\)
(iii) In \( \triangle \mathrm{AQB} \) and \( \triangle \mathrm{CPD} \),
\( \angle \mathrm{ABQ}=\angle \mathrm{CDP} \) (Alternate interior angles for \( \mathrm{AB} \| \mathrm{CD} \) )
\( \mathrm{AB}=\mathrm{CD} \) (Opposite sides of parallelogram ABCD\( ) \)
\(\mathrm{BQ}=\mathrm{DP}(\text { Given })\)
Two sides and included angle (SAS) Definition: Triangles are congruent if any pair of corresponding sides and their included angles are equal in both triangles.
\(\triangle \mathrm{AQB} \cong \triangle \mathrm{CPD}(\text { Using SAS congruence rule })\)
(iv) As we had observed that,
\(\triangle \mathrm{AQB} \cong \Delta \mathrm{CPD} \)
\(\mathrm{AQ}=\mathrm{CP}(\mathrm{CPCT})\)
(v) From the result obtained in (ii) and (iv),
\(\mathrm{AQ}=\mathrm{CP} \text { and } \mathrm{AP}=\mathrm{CQ}\)
Since,
Opposite sides in quadrilateral APCQ are equal to each other, APCQ is a parallelogram.
10. ABCD is a parallelogram and AP and CQ are perpendiculars from
vertices A and C on diagonal BD (see Fig. 8.21). Show that
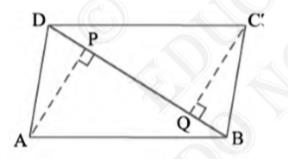
(i) \( \Delta \mathrm{APB} \cong \Delta \mathrm{CQD} \)
(ii) \( \mathrm{AP}=\mathrm{CQ} \)

(i) \( \Delta \mathrm{APB} \cong \Delta \mathrm{CQD} \)
(ii) \( \mathrm{AP}=\mathrm{CQ} \)
Answer
(i) In \( \triangle \mathrm{APB} \) and \( \triangle \mathrm{CQD}
\), \( \angle \mathrm{APB}=\angle \mathrm{CQD}\left(\right. \) Each \( \left.90^{\circ}\right) \)
\( \mathrm{AB}=\mathrm{CD} \) (Opposite sides of parallelogram ABCD\( ) \)
\( \angle \mathrm{ABP}=\angle \mathrm{CDQ} \) (Alternate interior angles for \( \mathrm{AB} \| \mathrm{CD} \) )
\( \Delta \mathrm{APB} \cong \Delta \mathrm{CQD} \) (By AAS congruency)
(ii) By using the above result
\( \Delta \mathrm{APB} \cong \Delta \mathrm{CQD} \), we obtain
CPCT: Corresponding parts of congruent triangles are congruent \( \mathrm{AP}=\mathrm{CQ}(\mathrm{By} \mathrm{CPCT}) \)
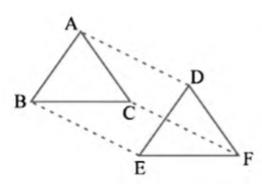
11. In \( \triangle \mathrm{ABC} \) and \( \Delta \mathrm{DEF},
\mathrm{AB}=\mathrm{DE}, \mathrm{AB} \| \mathrm{DE},
\mathrm{BC}=\mathrm{EF} \) and \( B C \| E F \). Vertices \( A, B
\) and \( C \) are joined to vertices \( D, E \) and \( F \)
respectively (see Fig. 8.22). Show that
(i) Quadrilateral \(ABED\) is a parallelogram
(ii) Quadrilateral \(BEFC\) is a parallelogram
(iii) \( \mathrm{AD} \| \mathrm{CF} \) and \( \mathrm{AD}=\mathrm{CF} \)
(iv) Quadrilateral \(ACFD\) is a parallelogram
(v) \( \mathrm{AC}=\mathrm{DF} \)
(vi) \( \Delta \mathrm{ABC} \cong \Delta \mathrm{DEF} \).
(i) Quadrilateral \(ABED\) is a parallelogram
(ii) Quadrilateral \(BEFC\) is a parallelogram
(iii) \( \mathrm{AD} \| \mathrm{CF} \) and \( \mathrm{AD}=\mathrm{CF} \)
(iv) Quadrilateral \(ACFD\) is a parallelogram
(v) \( \mathrm{AC}=\mathrm{DF} \)
(vi) \( \Delta \mathrm{ABC} \cong \Delta \mathrm{DEF} \).

Answer
(i) Given that: \( \mathrm{AB}=\mathrm{DE} \) and\( \mathrm{AB} \| \mathrm{DE} \)
If two opposite sides of a quadrilateral are equal and parallel to each other, then it will be a parallelogram.
Therefore, quadrilateral \(ABED\) is a parallelogram
(ii) Again,
\( \mathrm{BC}=\mathrm{EF} \) and \( \mathrm{BC} \| \mathrm{EF} \)
Therefore, quadrilateral \(BCEF\) is a parallelogram
(iii) As we had observed that \(ABED\) and \(BEFC\) are parallelograms
Therefore,
\( \mathrm{AD}=\mathrm{BE} \) and \( \mathrm{AD} \| \mathrm{BE} \)
(Opposite sides of a parallelogram are equal and parallel)
And,
\( \mathrm{BE}=\mathrm{CF} \) and \( \mathrm{BE} \| \mathrm{CF} \)
(Opposite sides of a parallelogram are equal and parallel)
\( \mathrm{AD}=\mathrm{CF} \) and \( \mathrm{AD} \| \mathrm{CF} \)
(iv) As we had observed that one pair of opposite sides ( AD and CF ) of quadrilateral
ACFD are equal and parallel to each other, therefore, it is a parallelogram
(v) As ACFD is a parallelogram, therefore, the pair of opposite sides will be equal and parallel to each other
\( \mathrm{AC} \| \mathrm{DF} \) and \( \mathrm{AC}=\mathrm{DF} \)
(vi) \( \triangle \mathrm{ABC} \) and \( \triangle \mathrm{DEF} \),
\( \mathrm{AB}=\mathrm{DE} \) (Given)
\( \mathrm{BC}=\mathrm{EF}( \) Given \( ) \)
\( \mathrm{AC}=\mathrm{DF}(\mathrm{ACFD} \) is a parallelogram \( ) \)
\( \Delta \mathrm{ABC} \cong \Delta \mathrm{DEF}(\mathrm{By} \) \(SSS\) congruence rule \( ) \)
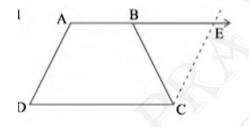
12. \(\mathrm{ABCD} \) is a trapezium in which \( \mathrm{AB} \|
\mathrm{CD} \) and \( \mathrm{AD}=\mathrm{BC} \) (see Fig. 8.23).
Show that
(i) \( \angle \mathrm{A}=\angle \mathrm{B} \)
(ii) \( \angle \mathrm{C}=\angle \mathrm{D} \)
(iii) \( \Delta \mathrm{ABC} \cong \Delta \mathrm{BAD} \)
(iv) Diagonal \( \mathrm{AC}= \) diagonal BD
[Hint: Extend \(AB\) and draw a line through \(C\) parallel to \(DA\) intersecting \(AB\) produced at \(E\) .]
(i) \( \angle \mathrm{A}=\angle \mathrm{B} \)
(ii) \( \angle \mathrm{C}=\angle \mathrm{D} \)
(iii) \( \Delta \mathrm{ABC} \cong \Delta \mathrm{BAD} \)
(iv) Diagonal \( \mathrm{AC}= \) diagonal BD
[Hint: Extend \(AB\) and draw a line through \(C\) parallel to \(DA\) intersecting \(AB\) produced at \(E\) .]

Answer
Let us extend \(AB \). Then, draw a line through \(C \), which is
parallel to \(AD \), intersecting \(AE\) at point \(E\)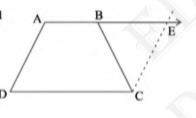
\( \mathrm{AD} \| \mathrm{CE} \) ( by construction) \( \mathrm{AE} \| \mathrm{DC} \) ( as AB is extended to E )It is clear that AECD is a parallelogram
(i) \( \mathrm{AD}=\mathrm{CE}( \) Opposite sides of parallelogram \(AECD) \)
However,
\( \mathrm{AD}=\mathrm{BC} \) (Given)
Therefore,
\(\mathrm{BC}=\mathrm{CE}\)
\( \angle \mathrm{CEB}=\angle \mathrm{CBE} \) (Angle opposite to equal sides are also equal)
Consider parallel lines \(AD\) and \(CE \). \(AE\) is the transversal line for them
\( \angle \mathrm{A}+\angle \mathrm{CEB}=180^{\circ} \) (Angles on the same side of transversal)
\( \angle \mathrm{A}+\angle \mathrm{CBE}=180^{\circ} \) (Using the relation \( \left.\mathrm{CEB}=\mathrm{CBE}\right) \ldots(1)\)
However,
\( \angle \mathrm{B}+\angle \mathrm{CBE}=180^{\circ} \) (Linear pair angles) \(\ldots(2)\)
From equations (1) and (2), we obtain
\(\angle \mathrm{A}=\angle \mathrm{B}\)
(ii) \( \mathrm{AB} \| \mathrm{CD} \)
\( \angle \mathrm{A}+\angle \mathrm{D}=180^{\circ} \) (Angles on the same side of the transversal)
Also,
\( \angle \mathrm{C}+\angle \mathrm{B}=180^{\circ} \) (Angles on the same side of the transversal)
\(\angle \mathrm{A}+\angle \mathrm{D}=\angle \mathrm{C}+\angle \mathrm{B}\)
However,
\( \angle \mathrm{A}=\angle \mathrm{B} \) [Using the result obtained in (i)
\(\angle C=\angle D\)
(iii) In \( \triangle \mathrm{ABC} \) and \( \triangle \mathrm{BAD} \),
\( \mathrm{AB}=\mathrm{BA}( \) Common side \( ) \)
\( \mathrm{BC}=\mathrm{AD} \) (Given)
\( \angle \mathrm{B}=\angle \mathrm{A} \) (Proved before)
\( \triangle \mathrm{ABC} \cong \triangle \mathrm{BAD} \) (SAS congruence rule)
(iv) We had observed that,
\( \triangle \mathrm{ABC} \cong \triangle \mathrm{BAD} \)
\( \mathrm{AC}=\mathrm{BD}(\mathrm{By} \mathrm{CPCT}) \)

