Ncert solutions for class 9 chapter Areas of Parallelograms and Triangles exercise 9.3 || class 9 exercise 9.3 || Areas of Parallelograms and Triangles class 9 exercise 9.3 || exercise 9.3 class 9 || exercise 9.3 class 9 maths || exercise 9.3 class 9 solutions || class 9 maths chapter 9 exercise 9.3 || class 9 Areas of Parallelograms and Triangles exercise 9.3
Explore clear, step-by-step solutions for Class 9 Maths Chapter 9, Exercise 9.3, which focuses on deepening students’ understanding of the area properties of triangles and parallelograms through logical proofs and geometric reasoning. This exercise emphasizes how figures on the same base and between the same parallels have equal areas. By solving these problems, students learn to apply fundamental geometric concepts to establish mathematical relationships between shapes. The tasks are designed to improve visual interpretation, strengthen logical analysis, and encourage precise proof-writing. Exercise 9.3 lays the groundwork for future topics like mensuration and coordinate geometry, while also building confidence in solving real-world geometry problems with clarity and accuracy.

ncert solutions for class 9 chapter Areas of Parallelograms and Triangles exercise 9.3 || class 9 exercise 9.3 || Areas of Parallelograms and Triangles class 9 exercise 9.3 || exercise 9.3 class 9 || exercise 9.3 class 9 maths || exercise 9.3 class 9 solutions || class 9 maths chapter 9 exercise 9.3 || class 9 Areas of Parallelograms and Triangles exercise 9.3
Exercise 9.3
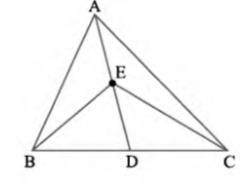
\( \operatorname{Area}(\triangle \mathrm{ABD})=\operatorname{Area}(\triangle \mathrm{ACD})\ldots(i)\)
ED is the median of \( \triangle \mathrm{EBC} \)
\( \operatorname{Area}(\triangle \mathrm{EBD})=\operatorname{Area}(\triangle \mathrm{ECD})\ldots(ii)\)
On subtracting equation (ii) from equation (i), we get,
\( \operatorname{Area}(\triangle \mathrm{ABD})-\operatorname{Area}(\mathrm{EBD})=\operatorname{Area}(\Delta \mathrm{ACD})-\operatorname{Area}(\Delta \mathrm{ECD}) \)
\( \operatorname{Area}(\triangle \mathrm{ABE})=\operatorname{Area}(\triangle \mathrm{ACE}) \)
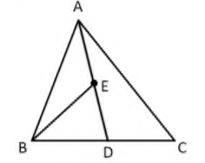
To prove: ar \( (\mathrm{BED})=\frac{ 1 }{ 4 } \) ar \( (\mathrm{ABC}) \).
Proof: AD is a median of \( \triangle \mathrm{ABC} \) and median divides a triangle into two triangles of equal area
\( \therefore \operatorname{ar}(\mathrm{ABD})=\operatorname{ar}(\mathrm{ACD}) \)
\( \Rightarrow \operatorname{ar}(\mathrm{ABD})=\frac{ 1 }{ 2 } \) ar \( (\mathrm{ABC}) \ldots(i)\)
In \( \Delta \mathrm{ABD} \),
BE is median (As E is mid-point of AD )
median divides a triangle into two triangles of equal area
\( \therefore \operatorname{ar}(\mathrm{BED})=\operatorname{ar}(\mathrm{BEA}) \)
\( \Rightarrow \operatorname{ar}(\mathrm{BED})=\frac{ 1 }{ 2 } \) ar \( (\mathrm{ABD}) \)
\( \Rightarrow \operatorname{ar}(\mathrm{BED})=\frac{ 1 }{ 2 } \times \frac{ 1 }{ 2 } \operatorname{ar}(\mathrm{ABC})( \text{from} (1): \operatorname{ar}(\mathrm{ABD})=\frac{ 1 }{ 2 } \operatorname{ar}(\mathrm{ABC})) \)
\( \Rightarrow \operatorname{ar}(\mathrm{BED})=\frac{ 1 }{ 4 } \mathrm{ar}(\mathrm{ABC}) \)
Hence proved.
\( B O \) is the median in \( \triangle A B C \). Therefore, it will divide it into two triangles of equal areas
Area \( (\triangle \mathrm{AOB})=\operatorname{Area}(\triangle \mathrm{BOC}) \ldots(i)\) In \( \triangle \mathrm{BCD} \),
CO is the median
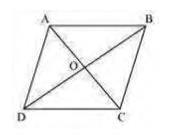
\( \operatorname{Area}(\Delta \mathrm{BOC})=\operatorname{Area}(\Delta \mathrm{COD})\ldots(ii)\)
Similarly, Area \( (\triangle \mathrm{COD})=\operatorname{Area}(\triangle \mathrm{AOD}) \ldots(iii)\)
From equations (i), (ii), and (iii), we obtain Area
\( (\Delta \mathrm{AOB})=\operatorname{Area}(\Delta \mathrm{BOC})=\operatorname{Area}(\Delta \mathrm{COD})=\operatorname{Area}(\Delta \mathrm{AOD}) \)
Therefore, it is evident that the diagonals of a parallelogram divide it into four triangles of equal area.
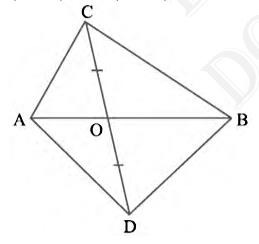
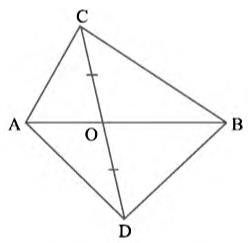
Consider \( \triangle \mathrm{ACD} \).
Line-segment CD is bisected by AB at \(O \). Therefore, \( AO\) is the median of \( \triangle \mathrm{ACD} \)
\( \operatorname{Area}(\triangle \mathrm{ACO})=\operatorname{Area}(\triangle \mathrm{ADO}) \ldots(i)\)
Considering \( \triangle \mathrm{BCD}, \mathrm{BO} \) is the median
\( \operatorname{Area}(\Delta \mathrm{BCO})=\operatorname{Area}(\Delta \mathrm{BDO}) \ldots(ii)\)
Adding equations (i) and (ii), we get
\( \operatorname{Area}(\triangle \mathrm{ACO})+\operatorname{Area}(\Delta \mathrm{BCO})=\operatorname{Area}(\triangle \mathrm{ADO})+\operatorname{Area}(\Delta \mathrm{BDO}) \)
\( \operatorname{Area}(\triangle \mathrm{ABC})=\operatorname{Area}(\Delta \mathrm{ABD}) \)
(i) \(BDEF\) is a parallelogram.
(ii) \( \operatorname{ar}(\mathrm{DEF})=\frac{1}{2} \operatorname{ar}(\mathrm{ABC}) \)
(iii) ar \( (\mathrm{BDEF})=\frac{1}{2} \) ar \( (\mathrm{ABC}) \)
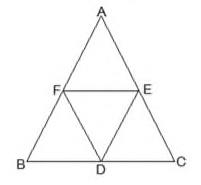
\( E F \) is parallel to \( B C \)
And,
The Midpoint Theorem states that the segment joining two sides of a triangle at the midpoints of those sides is parallel to the third side and is half the length of the third side.
\( \mathrm{EF}=\frac{1}{2} \mathrm{BC} \quad \) (By using Mid - point theorem)
Also,
\( \mathrm{BD}=\frac{1}{2} \mathrm{BC} \) (As D is the mid-point)
So,
\( \mathrm{BD}=\mathrm{EF} \)
BF and DE also parallel to each other
Therefore, the pair of opposite sides are equal and parallel in length.
Similarly, BF = DE
Therefore,
BDEF is a parallelogram
(ii) Diagonal of a parallelogram divides it into two equal area Therefore,
In parallelogram \(BDEF \)
\(DF\) is the diagonal
\( \Rightarrow \) Area of triangle \( \mathrm{BFD}= \) Area of triangle \(DEF \ldots(1)\)
In parallelogram \(DCEF\)
\(ED\) is the diagonal
\( \Rightarrow \) Area of triangle \( AFE = \) Area of triangle \(DEF \ldots(2)\)
In parallelogram \(AFDE\)
\(EF\) is the diagonal.
\( \Rightarrow \) Area of triangle \( \mathrm{CDE}= \) Area of triangle \(DEF \ldots(3)\)
So from (1), (2) and (3)
Area of triangle \( \mathrm{BFD}= \) Area of triangle \( \mathrm{AFE}= \) Area of triangle \( \mathrm{CDE}= \) Area of triangle \(DEF\)
Area of triangle \( \mathrm{ABC}= \) Area of triangle \( \mathrm{BFD}+ \) Area of triangle \( \mathrm{AFE}+ \) Area of triangle \(CDE +\) Area of triangle \(DEF\)
\(4 (\)Area of triangle \(DEF) = \) Area of triangle \(ABC\)
Area of triangle \( \mathrm{DEF}=\frac{1}{4} \times \) Area of triangle
(iii) Area of parallelogram \( \mathrm{BDEF}= \) Area of triangle \( \mathrm{DEF}+ \) Area of triangle \(BDE\)
From part (ii)
Area of parallelogram \(BDEF =\) Area of triangle \(DEF +\) Area of triangle \(DEF\)
\(=2 \times \text { Area of triangle DEF }\)
\(=2 \times \frac{1}{2} \times \text { Area of triangle } \mathrm{ABC}\)
\(=\frac{1}{2} \times \text { Area of triangle } \mathrm{ABC}\)
ncert solutions for class 9 chapter Areas of Parallelograms and Triangles exercise 9.3 || class 9 exercise 9.3 || Areas of Parallelograms and Triangles class 9 exercise 9.3 || exercise 9.3 class 9 || exercise 9.3 class 9 maths || exercise 9.3 class 9 solutions || class 9 maths chapter 9 exercise 9.3 || class 9 Areas of Parallelograms and Triangles exercise 9.3
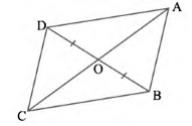
If \( \mathrm{AB}=\mathrm{CD} \), then show that:
(i) \( \operatorname{ar}(\mathrm{DOC})=\operatorname{ar}(\mathrm{AOB}) \)
(ii) ar \( (\mathrm{DCB})= \) ar \( (\mathrm{ACB}) \)
(iii) \( \mathrm{DA} \| \mathrm{CB} \) or ABCD is a parallelogram.
[Hint: From D and B, draw perpendiculars to AC]
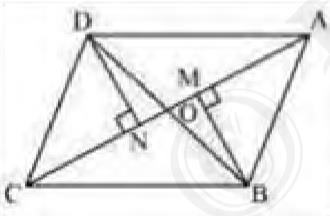
(i) In \( \triangle \mathrm{DON} \) and \( \triangle \mathrm{BOM} \),
\(\angle \mathrm{DNO}=\angle \mathrm{BMO} \quad\left(90^{\circ}\right)\)
\(\angle \mathrm{DON}=\angle \mathrm{BOM} \text { (Vertically opposite angles) }\)
\(\mathrm{OD}=\mathrm{OB} \text { (Given) }\)
By AAS congruence rule,
\(\Delta \mathrm{DON} \cong \Delta \mathrm{BOM}\)
\( \mathrm{DN}=\mathrm{BM} \quad(\mathrm{BY} CPCT) \ldots(i)) \)
We know that congruent triangles have equal areas.
\( \operatorname{Area}(\Delta \mathrm{DON})=\operatorname{Area}(\Delta \mathrm{BOM}) \ldots(ii)\)
In \( \triangle \mathrm{DNC} \) and \( \triangle \mathrm{BMA} \),
\( \angle \mathrm{DNC}=\angle \mathrm{BMA} \) (Angles made by perpendicular)
\( \mathrm{CD}=\mathrm{AB} \) (Given)
\( \mathrm{DN}=\mathrm{BM}[ \) Using equation (i)]
\( \triangle \mathrm{DNC} \cong \triangle \mathrm{BMA} \) (RHS congruence rule)
Area \( (\triangle \mathrm{DNC})= \) Area \( (\triangle \mathrm{BMA}) \ldots(iii)\)
Let us draw DN AC and BM AC
On adding equations (ii) and (iii), we obtain
\( \operatorname{Area}(\triangle \mathrm{DON})+\operatorname{Area}(\Delta \mathrm{DNC}) \)
\( =\operatorname{Area}(\Delta \mathrm{BOM})+\operatorname{Area}(\Delta \mathrm{BMA}) \)
Therefore,
\( \operatorname{Area}(\Delta \mathrm{DOC})=\operatorname{Area}(\Delta \mathrm{AOB}) \)
(ii) TO prove: \( \operatorname{Area}(\triangle \mathrm{DCB})=\operatorname{Area}(\triangle \mathrm{ACB}) \)
we have proved, Area \( (\triangle \mathrm{DOC})=\operatorname{Area}(\triangle \mathrm{AOB}) \)
\( \operatorname{Area}(\triangle \mathrm{DOC})+\operatorname{Area}(\triangle \mathrm{OCB})=\operatorname{Area}(\triangle \mathrm{AOB})+\operatorname{Area}(\triangle \mathrm{OCB}) \)
(Adding Area \( (\triangle \mathrm{OCB}) \) to both sides)
Area \( (\triangle \mathrm{DCB})=\operatorname{Area}(\triangle \mathrm{ACB}) \)
(iii)
We have proved above, \( \operatorname{Area}(\triangle \mathrm{DCB})=\operatorname{Area}(\triangle \mathrm{ACB}) \)
If two triangles have the same base and equal areas, then these will lie between the same parallels
So, \(DA \| CB \ldots(iv)\)
In quadrilateral \( A B C D \), one pair of opposite sides is equal \( (A B=C D) \) and the other pair of opposite sides is parallel (DA \( \| \mathrm{CB} \) )
Therefore, \( A B C D \) is a parallelogram
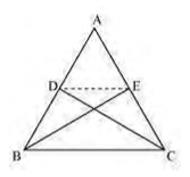
Since \( \triangle B C E \) and \( \triangle B C D \) are lying on a common base \( B C \) and also have equal areas,
\( \triangle \mathrm{BCE} \) and \( \triangle \mathrm{BCD} \) will lie between the same parallel lines
Therefore,
\( \mathrm{DE} \| \mathrm{BC} \)
Hence proved
In \( \triangle \mathrm{ABC}, \mathrm{XY}\|\mathrm{BC} \ \& \ \mathrm{BE}\| \mathrm{AC} \ \& \ \mathrm{CF} \| \mathrm{AB} \)
To prove: \( \operatorname{Ar}(\Delta \mathrm{ABE})=\operatorname{Ar}(\Delta \mathrm{ACF}) \)
Proof:
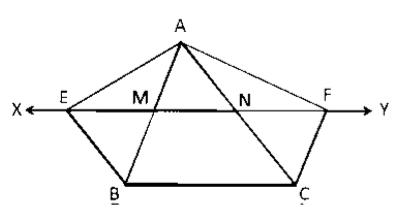
Let \(XY\) intersect \( \mathrm{AB} \ \& \ \mathrm{BC} \) at points M and N respectively.
The figure of the question is:
Now, \(XY || BC\)
And, we know that the parts of the parallel lines are parallel
\( \Rightarrow \mathrm{EN} \| \mathrm{BC} \ldots(1)\)
Also, it is given that \( \mathrm{BE} \| \mathrm{AC} \)
\( \Rightarrow \mathrm{BE} \| \mathrm{CN} \ldots(2)\)
From 1 and 2
\(BCNE\) is a parallelogram (because both the pair of opposite sides are parallel)
Now, the parallelogram \( \mathrm{BCNE} \& \triangle \mathrm{ABE} \) have a common base i.e. \( \mathrm{BE} \ \& BE\) is parallel to \(AC \).
\( \Rightarrow \operatorname{ar}(\triangle \mathrm{ABE})=1 / 2 \) area of parallelogram \(BCNE \ldots(i)\)
Similarly, we \(BCFM\) is also a parallelogram.
And, the \( \triangle \mathrm{ACF} \) and the parallelogram \( B C F M \) lie on the same base i.e. \(CF\)
\( \Rightarrow \operatorname{ar}(\triangle \mathrm{ACF})=\frac{1}{2} \) area of parallelogram \(BCFM \ldots(ii)\)
Now,
Parallelograms BCNE and BCFM are on the same base BC and between the same parallels BC and EF
hence there area will be equal.
\( \Rightarrow \operatorname{Area}(\mathrm{BCNE})=\operatorname{Area}(\mathrm{BCFM}) \ldots(iii) \)
From the equations (i), (ii) and (iii), we can write that, \( \operatorname{Ar}(\Delta \mathrm{ABE})=\operatorname{Ar}(\Delta \mathrm{ACF}) \)
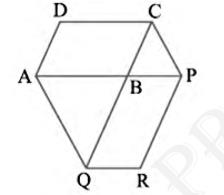
[Hint: Join AC and PQ. Now compare ar (ACQ) and ar (APQ)]
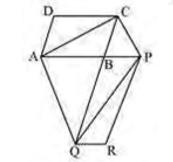
\( \triangle \mathrm{ACQ} \) and \( \triangle \mathrm{AQP} \) are on the same base \(AQ\) and between the same parallels \( A Q \) and \( C P \).
\( \operatorname{Area}(\triangle \mathrm{ACQ})=\operatorname{Area}(\triangle \mathrm{APQ}) \)
\( \operatorname{Area}(\triangle \mathrm{ACQ})-\operatorname{Area}(\triangle \mathrm{ABQ})\)
\(= \operatorname{Area}(\triangle \mathrm{APQ})-\operatorname{Area}(\triangle \mathrm{ABQ})\)
\( \operatorname{Area}(\triangle \mathrm{ABC})=\operatorname{Area}(\Delta \mathrm{QBP})\ldots(i)\)
Since AC and PQ are diagonals of parallelograms ABCD and PBQR respectively,
\( \operatorname{Area}(\triangle \mathrm{ABC})=\frac{1}{2} \operatorname{Area}(\mathrm{ABCD}) \ldots(ii)\)
\( \operatorname{Area}(\triangle \mathrm{QBP})=\frac{1}{2} \) Area \( (\mathrm{PBQR}) \ldots(iii)\)
From equations (i), (ii), and (iii), we obtain
\( \operatorname{Area}(\mathrm{ABCD})=\frac{1}{2} \operatorname{Area}(\mathrm{PBQR}) \)
Area \( (\mathrm{ABCD})=\operatorname{Area}(\mathrm{PBQR}) \)
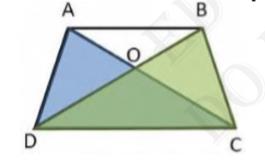
Area \( (\triangle \mathrm{DAC})=\operatorname{Area}(\triangle \mathrm{DBC})[ \) Area of triangles with same base and between the same parallels are equal in area.]
\( \operatorname{Area}(\triangle \mathrm{DAC})-\operatorname{Area}(\triangle \mathrm{DOC})=\operatorname{Area}(\Delta \mathrm{DBC})-\operatorname{Area}(\Delta \mathrm{DOC}) \)
\( \operatorname{Area}(\triangle \mathrm{AOD})=\operatorname{Area}(\Delta \mathrm{BOC}) \)
ncert solutions for class 9 chapter Areas of Parallelograms and Triangles exercise 9.3 || class 9 exercise 9.3 || Areas of Parallelograms and Triangles class 9 exercise 9.3 || exercise 9.3 class 9 || exercise 9.3 class 9 maths || exercise 9.3 class 9 solutions || class 9 maths chapter 9 exercise 9.3 || class 9 Areas of Parallelograms and Triangles exercise 9.3
(i) \( \operatorname{ar}(\mathrm{ACB})= \) ar \( (\mathrm{ACF}) \)
(ii) \( \operatorname{ar}(\mathrm{AEDF})= \) ar \( (\mathrm{ABCDE}) \)
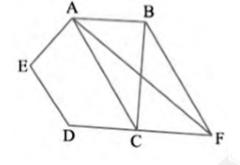
\( \operatorname{Area}(\triangle \mathrm{ACB})=\operatorname{Area}(\triangle \mathrm{ACF}) \)
(ii) It can be observed that:
\(\operatorname{Area}(\triangle \mathrm{ACB})=\operatorname{Area}(\triangle \mathrm{ACF})\)
\(\text { Area }(\triangle \mathrm{ACB})+\text { Area }(\mathrm{ACDE})=\text { Area }(\mathrm{ACF})+\text { Area }(\mathrm{ACDE})\)
\(\text { Area }(\mathrm{ABCDE})=\text { Area }(\mathrm{AEDF})\)
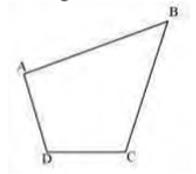
Join diagonal BD and draw a line parallel to BD through point A .
Let it meet the extended side \( C D \) of \( A B C D \) at point \( E \). Join \( B E \) and \( A D \). Let them intersect each other at \( O \). Then, portion \( \triangle A O B \) can be cut from the original field so that the new shape of the field will be \( \triangle B C E \)
We have to prove that the area of \( \triangle \mathrm{AOB} \) (portion that was cut so as to construct Health Centre)
is equal to the area of \( \triangle \mathrm{DEO} \) (portion added to the field so as to make the area of the new field so formed equal to the area of the original field)
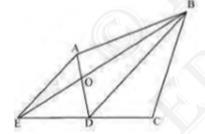
It can be observed that \( \triangle \mathrm{DEB} \) and \( \triangle \mathrm{DAB} \) lie on the same base BD and are between the same parallels BD and AE
So,
Area \( (\triangle \mathrm{DEB})=\operatorname{Area}(\triangle \mathrm{DAB}) \)
\( \operatorname{Area}(\triangle \mathrm{DEB})-\operatorname{Area}(\triangle \mathrm{DOB})=\operatorname{Area}(\triangle \mathrm{DAB})-\operatorname{Area}(\Delta \mathrm{DOB}) \)
\( \operatorname{Area}(\triangle \mathrm{DEO})=\operatorname{Area}(\triangle \mathrm{AOB}) \)
[Hint: Join CX]
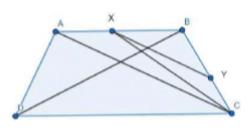
It can be observed that \( \triangle \mathrm{ADX} \) and \( \triangle \mathrm{ACX} \) lie on the same base \(AX\) and are between the same parallels \(AB\) and \(DC\) .
\( \operatorname{Area}(\triangle \mathrm{ADX})=\operatorname{Area}(\triangle \mathrm{ACX}) \ldots(i)\)
\( \triangle \mathrm{ACY} \) and \( \triangle \mathrm{ACX} \) lie on the same base \(AC\) and are between the same parallels AC and \(XY\)
Area \( (\triangle \mathrm{ACY})=\operatorname{Area}(\mathrm{ACX}) \ldots(ii)\)
From equations (i) and (ii), we obtain
\( \operatorname{Area}(\triangle \mathrm{ADX})=\operatorname{Area}(\triangle \mathrm{ACY}) \)
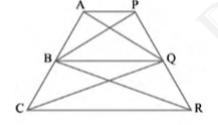
\( \operatorname{Area}(\triangle \mathrm{ABQ})=\operatorname{Area}(\Delta \mathrm{PBQ}) \ldots(i)\)
Again, \( \triangle \mathrm{BCQ} \) and \( \triangle \mathrm{BRQ} \) lie on the same base BQ and are between the same parallels BQ and CR
\( \operatorname{Area}(\triangle \mathrm{BCQ})=\operatorname{Area}(\triangle \mathrm{BRQ}) \ldots(ii)\)
On adding equations (i) and (ii), we obtain
\( \operatorname{Area}(\triangle \mathrm{ABQ})+\operatorname{Area}(\triangle \mathrm{BCQ})=\operatorname{Area}(\Delta \mathrm{PBQ})+\operatorname{Area}(\Delta \mathrm{BRQ}) \)
\( \operatorname{Area}(\triangle \mathrm{AQC})=\operatorname{Area}(\triangle \mathrm{PBR}) \)
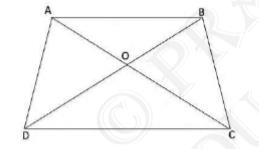
It is given that:
\( \operatorname{Area}(\Delta \mathrm{AOD})=\operatorname{Area}(\Delta \mathrm{BOC}) \)
add area \( (\mathrm{AOB}) \) to both sides,
\( \operatorname{Area}(\triangle \mathrm{AOD})+\operatorname{Area}(\triangle \mathrm{AOB})=\operatorname{Area}(\triangle \mathrm{BOC})+\operatorname{Area}(\triangle \mathrm{AOB}) \)
\( \Rightarrow \operatorname{Area}(\triangle \mathrm{ADB})=\operatorname{Area}(\triangle \mathrm{ACB}) \)
We know that triangles on the same base having areas equal to each other lie between the same parallels
Therefore, these triangles, \( \triangle \mathrm{ADB} \) and \( \triangle \mathrm{ACB} \), are lying between the same parallels i.e.,
\( \mathrm{AB} \| \mathrm{CD} \)
Therefore, \( A B C D \) is a trapezium.
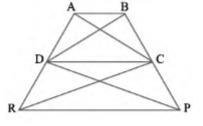
Area \( (\Delta \mathrm{DRC})=\operatorname{Area}(\Delta \mathrm{DPC}) \)
As \( \triangle \mathrm{DRC} \) and \( \triangle \mathrm{DPC} \) lie on the same base DC and have equal areas, therefore, they must lie between the same parallel lines
\( \mathrm{DC} \| RP\)
Therefore, DCPR is a trapezium. It is
Also given that:
Area \( (\triangle \mathrm{BDP})=\operatorname{Area}(\triangle \mathrm{ARC}) \)
Area \( (\mathrm{BDP})-\operatorname{Area}(\triangle \mathrm{DPC})=\operatorname{Area}(\triangle \mathrm{ARC})-\operatorname{Area}(\Delta \mathrm{DRC}) \)
Area \( (\triangle \mathrm{BDC})=\operatorname{Area}(\triangle \mathrm{ADC}) \)
Since \( \triangle \mathrm{BDC} \) and \( \triangle \mathrm{ADC} \) are on the same base CD and have equal areas, they must lie between the same parallel lines
\( \mathrm{AB} \| \mathrm{CD} \)
Therefore,
ABCD is a trapezium.

