Class 9 exercise 10.3 || exercise 10.3 class 9 solutions || ncert solutions for class 9 chapter circles exercise 10.3 || exercise 10.3 class 9 maths || exercise 10.3 class 9 || class 9 circles exercise 10.3 || class 9 maths chapter 10 exercise 10.3 || circles class 9 exercise 10.3
Explore clear, step-by-step solutions for Class 9 Maths Chapter 10, Exercise 10.3, which deepens students’ understanding of the geometry of circles through practical theorems and reasoning. This exercise emphasizes key concepts such as the angle subtended by a chord at a point on the circle, the angles in the same segment and the cyclic nature of quadrilaterals. Students are guided to observe and prove important relationships between arcs, angles and chords using precise constructions and deductive logic. Exercise 10.3 not only sharpens critical thinking and visual interpretation skills but also builds a solid foundation for future topics like coordinate geometry, circle theorems, and real-world applications involving arcs and angles.
class 9 exercise 10.3 || exercise 10.3 class 9 solutions || ncert solutions for class 9 chapter circles exercise 10.3 || exercise 10.3 class 9 maths || exercise 10.3 class 9 || class 9 circles exercise 10.3 || class 9 maths chapter 10 exercise 10.3 || circles class 9 exercise 10.3
Exercise 10.3
class 9 exercise 10.3 || exercise 10.3 class 9 solutions || ncert solutions for class 9 chapter circles exercise 10.3 || exercise 10.3 class 9 maths || exercise 10.3 class 9 || class 9 circles exercise 10.3 || class 9 maths chapter 10 exercise 10.3 || circles class 9 exercise 10.3
1. Draw different pairs of circles. How many points does each
pair have in common? What is the maximum number of common
points?
Answer
Consider the following pair of circles
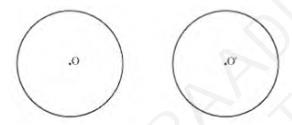
The above circles do not intersect each other at any point. Therefore, they do not have any point in common
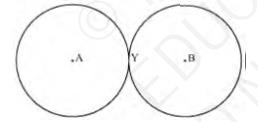
The above circles touch each other only at one-point Y. Therefore, there is 1 point in common
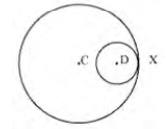
The above circles touch each other at 1-point X only. Therefore, the circles have 1 point in common
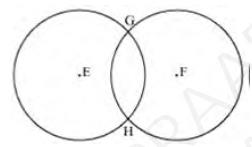
These circles intersect each other at two points G and H.
Therefore, the circles have two points in common. It can be observed that there can be a maximum of 2 points in common.
2. Suppose you are given a circle. Give a construction to find
its centre.
Answer
The below given steps will be followed to find the centre of the
given circle
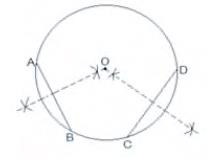
Step 1. Take the given circle
Step 2. Take any two different chords AB and CD of this circle and draw perpendicular bisectors of these chords
Step 3. Let these perpendicular bisectors meet at point \( O \).
Hence, \( O \) is the centre of the given circle
class 9 exercise 10.3 || exercise 10.3 class 9 solutions || ncert solutions for class 9 chapter circles exercise 10.3 || exercise 10.3 class 9 maths || exercise 10.3 class 9 || class 9 circles exercise 10.3 || class 9 maths chapter 10 exercise 10.3 || circles class 9 exercise 10.3
3. If two circles intersect at two points, prove that their
center lie on the perpendicular bisector of the common chord.
Answer
Let two circles with centres \( O \) and \( O^{\prime} \)
respectively intersect at two points A and Bsuch that \( A B \) is the common chord of two circles and \( O O^{\prime} \) is the line segment joining the centres, as shown in the figure:
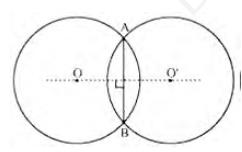
Also, AB is the chord of the circle centered at O. Therefore, the perpendicular bisector of \( A B \) will pass through \( O \).
Let \( {OO}^{\prime} \) intersect AB at M. Also, draw line segments \( {OA}, {OB}, {O}^{\prime} {A} \) and \(O^{\prime}B\).
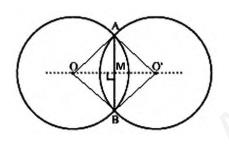
Now, In \( \triangle {OAO}^{\prime} \) and \( {OBO}^{\prime} \),
\( {OA}={OB} \) (radii of same circle) \( {O}^{\prime} {A}={O}^{\prime} {B} \) (radii of same circle) \( {O}^{\prime} {O} \) (common side)
\( \Rightarrow \Delta {OAO}^{\prime} \cong \Delta {OBO}^{\prime} \) (Side-Side-Side congruency)
\( \Rightarrow \angle {AOO}^{\prime}=\angle {BOO}^{\prime}\)
\( \Rightarrow \angle {AOM}=\angle {BOM} \quad \ldots\ldots\text{(i)}\)
Now in \( \triangle {AOM} \) and \( \triangle {BOM} \) we have \( {OA}={OB} \) (radii of same circle)
\( \angle A O M=\angle B O M \) (from (i)) OM \( ={OM} \) (common side)
\( \Rightarrow \triangle {AOM} \cong \triangle {BOM} \) (Side-Angle-Side congruency)
\( \Rightarrow {AM}={BM} \) and \( \angle {AMO}=\angle {BMO} \) but \( \angle {AMO}+\angle {BMO}=180^{\circ} \)
\( \Rightarrow 2 \angle {AMO}=180^{\circ} \)
\( \Rightarrow \angle {AMO}=90^{\circ} \)
Thus, \( {AM}={BM} \) and \( \angle {AMO}=\angle {BMO}=90^{\circ} \)
Hence \( O O^{\prime} \) is the perpendicular bisector of \( A B \).
