Ex 11.1 Class 12 Maths Ncert Solutions

Let the direction cosines of the line making \( \angle \alpha \) with x-axis, \( \beta \) - with y-axis and \( \gamma \) - with z-axis are \( l, \mathrm{~m} \) and n
\( \Rightarrow l=\cos \alpha, \mathrm{m}=\cos \beta \) and \( \mathrm{n}=\cos \gamma \)
Here \( \alpha=90^{\circ}, \beta=135^{\circ} \) and \( \gamma=45^{\circ} \)
So direction cosines are
\( l=\cos 90^{\circ}=0 \)
\( m=\cos 135^{\circ}=\cos \left(180^{\circ}-45^{\circ}\right)=-\cos 45^{\circ}=\frac{-1}{\sqrt{2}} \)
\( \mathrm{n}=\cos 45^{\circ}=\frac{1}{\sqrt{2}} \)
\( \Rightarrow \) Direction cosines of the line \( 0, \frac{-1}{\sqrt{2}}, \frac{1}{\sqrt{2}} \)

Let the direction cosines of the line making \( \angle \alpha \) with x-axis, \( \beta \) - with y-axis and \( \gamma \) - with z-axis are \( l, \mathrm{~m} \) and n
\( \Rightarrow l=\cos \alpha, \mathrm{m}=\cos \beta \) and \( \mathrm{n}=\cos \gamma \)
Here given \( \alpha=\beta=\gamma \) (line makes equal angles with the coordinate axes) \(\ldots(1) \)
Direction Cosines are
\( \Rightarrow l=\cos \alpha, \mathrm{m}=\cos \beta \) and \( \mathrm{n}=\cos \gamma \)
We have
\( l^{2}+\mathrm{m}^{2}+\mathrm{n}^{2}=1 \)
\( \cos ^{2} \alpha+\cos ^{2} \beta+\cos ^{2} \gamma=1 \)
From 1 we have
\( \cos ^{2} \alpha+\cos ^{2} \alpha+\cos ^{2} \alpha=1 \)
\( 3 \cos ^{2} \alpha=1 \)
\( \cos \alpha= \pm \sqrt{\frac{1}{3}} \)
The direction cosines are
\( l= \pm \sqrt{\frac{1}{3}}, m= \pm \sqrt{\frac{1}{3}} n= \pm \sqrt{\frac{1}{3}} \)

If the direction ratios of the line are \( \mathrm{a}, \mathrm{b} \) and c
Then the direction cosines are \( \frac{a}{\sqrt{a^{2}+b^{2}=c^{2}}}, \frac{b}{\sqrt{a^{2}+b^{2}=c^{2}}}, \frac{c}{\sqrt{a^{2}+b^{2}=c^{2}}} \)
Given direction ratios are \( -18,12 \) and -4
\( \Rightarrow \mathrm{a}=-18, \mathrm{~b}=12 \) and \( \mathrm{c}=-4 \)
\( \sqrt{a^{2}+b^{2}=c^{2}}=\sqrt{(-18)^{2}+12^{2}=(-4)^{2}} \)
\(=\sqrt{324+144+16}\)
\(=\sqrt{484}=22\)
Direction cosines are
\(\frac{-18}{22}, \frac{12}{22}, \frac{-4}{22}=\frac{-9}{11}, \frac{6}{11}, \frac{-2}{11}\)

If the direction ratios of two lines segments are proportional, then the lines are collinear.
Given A \( (2,3,4) \), B \( (-1,-2,1) \), C \( (5,8,7) \)
Direction ratio of line joining \( A(2,3,4) \) and \( B(-1,-2,1) \), are
\((-1-2),(-2-3),(1-4)\)
\(=(-3,-5,-3)\)
So \( \mathrm{a}_{1}=-3, \mathrm{~b}_{1}=-5, \mathrm{c}_{1}=-3 \)
Direction ratio of line joining \( B(-1,-2,1) \) and \( C(5,8,7) \) are
\((5-(-1)),(8-(-2)),(7-1)\)
\(=(6,10,6)\)
So \( \mathrm{a}_{2}=6, \mathrm{~b}_{2}=10 \) and \( \mathrm{c}_{2}=6 \)
It is clear that the direction ratios of AB and BC are of same proportions
As
\(\frac{a_{1}}{a_{2}}=\frac{-3}{6}=-2\)
\(\frac{b_{1}}{b_{2}}=\frac{-5}{10}=-2\)
And \( \frac{c_{1}}{c_{2}}=\frac{-3}{6}=-2 \)
Therefore, A, B, C are collinear.

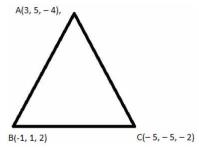
The direction cosines of the two points passing through \( \mathrm{A}\left(x_{1}, y_{1}, z_{1}\right) \) and B \( \left(x_{2}, y_{2}, z_{2}\right) \) is given by
\(
\left(x_{2}-x_{1}\right),\left(y_{2}-y_{1}\right),\left(z_{2}-z_{1}\right)
\)
And the direction cosines of the line AB is \( \frac{\left(x_{2}-x_{1}\right)}{\mathrm{AB}}, \frac{\left(y_{2}-y_{1}\right)}{\mathrm{AB}}, \frac{\left(z_{2}-z_{1}\right)}{\mathrm{AB}} \)
Where \( \mathrm{AB}=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}+\left(z_{2}-z_{1}\right)^{2}} \)
\(\begin{array}{|l|l|l|}
\hline Here \ \mathrm{A}=(3,5,-4) & \mathrm{B}=(-1,1,2) & \mathrm{C}=(-5,-5,-2) \\
\hline \mathrm{B}=(-1,1,2) & \mathrm{C}=(-5,-5,-2) & \mathrm{A}=(3,5,-4) \\
\hline \text{Direction ratios of AB} & \text{Direction ratios of BC} & \text{Direction ratios of CA} \\
\hline (-1-3),(1-5),(2-(-4)) & (-5+1),(-5-1),(-2-2) & (3+5),(5+5),(-4+2) \\
\hline =-4,-4,6 & =(-4,-6,-4) & =(8,10,-2) \\
\hline \sqrt{\mathrm{AB}}=\sqrt{(68)}=2 \sqrt{17} & \sqrt{\mathrm{BC}}=\sqrt{(68)}=2 \sqrt{17} & \sqrt{\mathrm{CA}}=\sqrt{(168)}=2 \sqrt{42} \\
\hline \text{Direction Cosines of} & \text{Direction Cosines of BC} & \text{Direction Cosines of CA} \\
AB \ \text{are} & \text{are} & \text{are} \\
\frac{-4}{2 \sqrt{17}}, \frac{-4}{2 \sqrt{17}}, \frac{6}{2 \sqrt{17}} , & \frac{-4}{2 \sqrt{17}}, \frac{-6}{2 \sqrt{17}}, \frac{-4}{2 \sqrt{17}} , & \frac{8}{2 \sqrt{42}}, \frac{10}{2 \sqrt{42}}, \frac{-2}{2 \sqrt{42}} , \\
\frac{-2}{\sqrt{17}}, \frac{-2}{\sqrt{17}}, \frac{3}{\sqrt{17}} & \frac{-2}{\sqrt{17}}, \frac{-3}{\sqrt{17}}, \frac{-2}{\sqrt{17}} & \frac{4}{\sqrt{42}}, \frac{5}{\sqrt{42}}, \frac{1}{\sqrt{42}} \\
\hline
\end{array} \)