Class 11 Chapter 2 Exercise 2.1 Solution

Given: \( \left(\frac{x}{3}+1, y-\frac{2}{3}\right)=\left(\frac{5}{3}, \frac{1}{3}\right) \)
Since the ordered pairs are equal, the corresponding elements are equal.
Therefore, \( \frac{x}{3}+1=\frac{5}{3} \) and \( y-\frac{2}{3}=\frac{1}{3} \)
\(\frac{x}{3}=\frac{5}{3}-1 \text { and } y=\frac{1}{3}+\frac{2}{3}\)
\(\frac{x}{3}=\frac{5-3}{3} \text { and } y=\frac{1+2}{3}\)
\(\frac{x}{3}=\frac{2}{3} \quad \text { and } y=\frac{3}{3}\)
Hence by solving we get, \( x=2 \) and \( y=1 \).

Given: Set A has 3 elements and the set \( \mathrm{B}=\{3,4,5\} \)
As we see the number of elements in set \( \mathrm{B}=3 \).
Number of elements in \( (A \times B)=( \) Number of elements in set \( A) \times \) (Number of elements in B)
\(\Rightarrow \mathrm{n}(\mathrm{A} \times \mathrm{B})=\mathrm{n}(\mathrm{A}) \times \mathrm{n}(\mathrm{B})\)
\(\Rightarrow \mathrm{n}(\mathrm{A} \times \mathrm{B})=3 \times 3\)
\(\Rightarrow \mathrm{n}(\mathrm{A} \times \mathrm{B})=9\)
Hence, the number of elements in \( (A \times B)=9 \).

Given: \( \mathrm{G}=\{7,8\} \) and \( \mathrm{H}=\{5,4,2\} \)
By definition of Cartesian product of two non-empty Set \(P\) and \(Q\) :
\(P \times Q=\{(p, q): p \in P, q \in Q\}\)
Therefore, \( \mathrm{G} \times \mathrm{H}=\{(7,5),(7,4),(7,2),(8,5),(8,4),(8,2)\} \).
And \( \mathrm{H} \times \mathrm{G}=\{(5,7),(5,8),(4,7),(4,8),(2,7),(2,8)\} \).

(i) Given: \( \mathrm{P}=\{\mathrm{m}, \mathrm{n}\} \) and \( \mathrm{Q}=\{\mathrm{n}, \mathrm{m}\} \)
By definition of Cartesian product of two non-empty Set \(P\) and \(Q\) :
\(P \times Q=\{(p, q): p \in P, q \in Q\}\)
Therefore, \( P \times Q=\{(m, n),(m, m),(n, m),(n, n)\} \).
\(\Rightarrow \mathrm{P} \times \mathrm{Q} \neq\{(\mathrm{m}, \mathrm{n}),(\mathrm{n}, \mathrm{m})\}\)
Hence, the statement is false.
(ii) Given: A and B are non-empty sets and \( x \in \mathrm{A} \) and \( y \in \mathrm{B} \).
By definition of Cartesian product of two non-empty Set P and Q :
\(\mathrm{P} \times \mathrm{Q}=\{(\mathrm{p}, \mathrm{q}): \mathrm{p} \in \mathrm{P}, \mathrm{q} \in \mathrm{Q}\}\)
\(\Rightarrow \mathrm{A} \times \mathrm{B}=\{(x, y): x \in \mathrm{A}, y \in \mathrm{B}\}\)
Hence, the statement is true.
(iii) Given: \( \mathrm{A}=\{1,2\}, \mathrm{B}=\{3,4\} \)
To Prove: \( \mathrm{A} \times(\mathrm{B} \cap \phi)=\phi \).
As \( (B \cap \phi)=\phi \)
By definition if either of the two set P and Q is null set then \( \mathrm{P} \times \mathrm{Q} \) will also be a null set. i.e. \( \mathrm{P} \times \mathrm{Q}=\phi \).
\(\Rightarrow \mathrm{A} \times(\mathrm{B} \cap \phi)=\phi\)
Hence, the statement is true.

Given: \( \mathrm{A}=\{-1,1\} \)
Cartesian product of a two sets A and B is given by set of multiplication of every member of the set with every other member of the set. Thus pairs of members of set are formed.
For given \( \mathrm{A}, \mathrm{A} \times \mathrm{A}=\{-1,1\} \times\{-1,1\} \)
\(\mathrm{A} \times \mathrm{A}=\{(-1,-1),(-1,1),(1,-1),(1,1)\}\)
Now,
By definition \( \mathrm{A} \times \mathrm{A} \times \mathrm{A}=\{(\mathrm{a}, \mathrm{b}, \mathrm{c}): \mathrm{a}, \mathrm{b}, \mathrm{c} \in \mathrm{A}\} \).
\(\Rightarrow \mathrm{A} \times \mathrm{A} \times \mathrm{A}=\{(-1,-1,-1),(-1,-1,1),(-1,1,-1),(1,-1,-1),(-1,1,1)\)
\((1,-1,1),(1,1,-1),(1,1,1)\}\)

Given: \( \mathrm{A} \times \mathrm{B}=\{(\mathrm{a}, x),(\mathrm{a}, y),(\mathrm{b}, x),(\mathrm{b}, y)\} \)
By definition of Cartesian product of two non-empty Set \(P\) and \(Q\) :
\(P \times Q=\{(p, q): p \in P, q \in Q\}\)
Hence, we see \( \mathrm{A}= \) set of all first elements.
\( B= \) set of all second elements.
\( \Rightarrow \mathrm{A}=\{\mathrm{a}, \mathrm{b}\} \) and \( \mathrm{B}=\{x, y\} \).

Given: \( \mathrm{A}=\{1,2\}, \mathrm{B}=\{1,2,3,4\}, \mathrm{C}=\{5,6\} \) and \( \mathrm{D}=\{5,6,7,8\} \)
To verify: \( A \times(B \cap C)=(A \times B) \cap(A \times C) \)
As we see, \( \mathrm{B} \cap \mathrm{C}=\{1,2,3,4\} \cap\{5,6\}=\phi \).
By definition if either of the two set P and Q is null set then \( \mathrm{P} \times \mathrm{Q} \) will also be a null set. i.e. \( \mathrm{P} \times \mathrm{Q}=\phi \).
\( A \times(B \cap C)=\phi \ldots (1\) )
Now, \( (\mathrm{A} \times \mathrm{B})=\{(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4)\} \)
And \( (\mathrm{A} \times \mathrm{C})=\{(1,5),(1,6),(2,5),(2,6)\} \)
\( (\mathrm{A} \times \mathrm{B}) \cap(\mathrm{A} \times \mathrm{C})=\phi \ldots(2) \)
From (1) and (2)
\( A \times(B \cap C)=(A \times B) \cap(A \times C) \)

Given: \( \mathrm{A}=\{1,2\}, \mathrm{B}=\{1,2,3,4\}, \mathrm{C}=\{5,6\} \) and \( \mathrm{D}=\{5,6,7,8\} \)
To verify: \( A \times C \) is a subset of \( B \times D \).
\((\mathrm{A} \times \mathrm{C})=\{(1,5),(1,6),(2,5),(2,6)\}\)
\((\mathrm{B} \times \mathrm{D})=\{(1,5),(1,6),(1,7),(1,8),(2,5),(2,6),(2,7),(2,8),(3,5),(3,6),\)
\((3,7),(3,8),(4,5),(4,6),(4,7),(4,8)\}\)
As we see all the elements of set \( A \times B \) are there in set \( B \times D \).
Hence, \( A \times C \) is a subset of \( B \times D \).

Given: \( \mathrm{A}=\{1,2\} \) and \( \mathrm{B}=\{3,4\} \)
\((\mathrm{A} \times \mathrm{B})=\{(1,3),(1,4),(2,3),(2,4)\}\)
Number of elements in \( (A \times B)=4 \)
\(\Rightarrow \mathrm{n}(\mathrm{A} \times \mathrm{B})=4\)
Then number of subsets of \( \operatorname{set}(A \times B)=2 n=24=16 \)
\( \Rightarrow \) number of subsets of \( \operatorname{set}(A \times B)=16 \)
These are:
\(\{\phi\},\{(1,3)\},\{(1,4)\},\{(2,3)\},\{(2,4)\},\{(1,3),(1,4)\},\{(1,3),(2,3)\},\)
\(\{(1,3),(2,4)\},\{(1,4),(2,3)\},\{(1,4),(2,4)\},\{(2,3),(2,4)\},\{(1,3),(1,4)\)
\((2,3)\},\{(1,3),(1,4),(2,4)\},\{(1,4),(2,3),(2,4)\},\{(1,3),(2,3),(2,4)\}\)
\(\{(1,3),(1,4),(2,3),(2,4)\} .\)

Given: \( \mathrm{n}(\mathrm{A})=3 \) and \( \mathrm{n}(\mathrm{B})=2 \) and If \( (x, 1),(y, 2),(z, 1) \) are in \( \mathrm{A} \times \mathrm{B} \).
By definition of Cartesian product of two non-empty Set P and Q : \( P \times Q=\{(p, q): p \in P, q \in Q\} \)
It means graphically as,

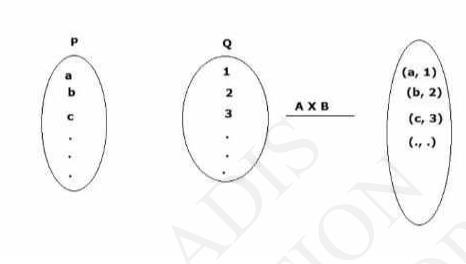
Hence, we see \( \mathrm{P}= \) set of all first elements.
\( \mathrm{Q}= \) set of all second elements.
\( \Rightarrow(x, y, z) \) are elements of A and \( (1,2) \) are elements of B .
\( \Rightarrow \mathrm{As} \mathrm{n}(\mathrm{A})=3 \) and \( \mathrm{n}(\mathrm{B})=2 \) so, \( \mathrm{A}=\{x, y, z\} \) and \( \mathrm{B}=\{1,2\} \).

Given: Cartesian product \( \mathrm{A} \times \mathrm{A} \) having 9 elements among which are found \( (-1,0) \) and \( (0,1) \).
Number of elements in \( (A \times B)=( \) Number of elements in set \( A) \times \) (Number of elements in B)
\(\Rightarrow \mathrm{n}(\mathrm{A} \times \mathrm{A})=\mathrm{n}(\mathrm{A}) \times \mathrm{n}(\mathrm{A})\)
\(\Rightarrow \mathrm{n}(\mathrm{A} \times \mathrm{A})=9 \text { (given) }\)
\(\Rightarrow \mathrm{n}(\mathrm{A}) \times \mathrm{n}(\mathrm{A})=9\)
\(\Rightarrow \mathrm{n}(\mathrm{A})=3\)
By definition \( \mathrm{A} \times \mathrm{A}=\{(\mathrm{a}, \mathrm{a}): \mathrm{a} \in \mathrm{A}\} \).
Therefore, \( -1,0 \) and 1 are the elements of set A .
Because, \( \mathrm{n}(\mathrm{A})=3 \) therefore, \( \mathrm{A}=\{-1,0,1\} \).
Hence the remaining elements of set \( (\mathrm{A} \times \mathrm{A}) \) are: \( (-1,-1),(-1,1),(0,0),(0,-1),(1,1),(1,-1) \) and \( (1,0) \).