class 11 ch 2 exercise 2.2 solutions || class 11 maths ncert solutions || ncert solutions for class 11 maths chapter 2 || class 11 maths relations and functions || ncert exemplar class 11 maths || exercise 2.2 class 11 maths solutions || class 11 chapter 2 exercise 2.2 solution
Searching for Class 11 Maths NCERT Solutions for Exercise 2.2? You’ve come to the perfect place! Here, you’ll find detailed and easy-to-follow solutions for every question from Chapter 2 – Relations and Functions, Exercise 2.2. This part of the chapter focuses on important concepts that lay the groundwork for deeper mathematical studies. The solutions provided are completely in line with the latest CBSE syllabus, making your exam preparation more effective. Reviewing Exercise 2.2 carefully will not only boost your understanding but also improve your problem-solving abilities in this foundational area of mathematics.

class 11 ch 2 exercise 2.2 solutions || class 11 maths ncert solutions || ncert solutions for class 11 maths chapter 2 || class 11 maths relations and functions || ncert exemplar class 11 maths || exercise 2.2 class 11 maths solutions || class 11 chapter 2 exercise 2.2 solution
Exercise 2.2
1. Let \( \mathrm{A}=\{1,2,3, \ldots, 14\} \). Define a relation R from A to A by \( \mathrm{R}= \) \( \{(x, y): 3 x-y=0 \), where \( x, y \in \mathrm{A}\} \). Write down its domain, codomain and range.
Answer
Given: \( \mathrm{A}=\{1,2,3, \ldots, 14\} \) and \( \mathrm{R}=\{(x, y): 3 x-y=0 \), where \( x, y \in \mathrm{A}\} \)
As the relation R from A to A is given as:
\( \mathrm{R}=\{(x, y): 3 x-y=0 \), where \( x, y, \mathrm{~A}\} \)
\( \Rightarrow \mathrm{R}=\{(x, y): 3 x=y \), where \( x, y, \mathrm{~A}\} \)
Hence the relation in roaster form, \( \mathrm{R}=\{(1,3),(2,6),(3,9),(4,12)\} \)
As Domain of \( \mathrm{R}= \) set of all first elements of the order pairs in the relation.
\( \Rightarrow \) Domain of \( \mathrm{R}=\{1,2,3,4\} \)
Codomain of \( \mathrm{R}= \) the whole set A
\( \Rightarrow \) Codomain of \( \mathrm{R}=\{1,2,3, \ldots, 14\} \)
Range of \( \mathrm{R}= \) set of all second elements of the order pairs in the relation.
\( \Rightarrow \) range of \( \mathrm{R}=\{3,6,9,12\} \).
class 11 ch 2 exercise 2.2 solutions || class 11 maths ncert solutions || ncert solutions for class 11 maths chapter 2 || class 11 maths relations and functions || ncert exemplar class 11 maths || exercise 2.2 class 11 maths solutions || class 11 chapter 2 exercise 2.2 solution
2. Define a relation R on the set N of natural numbers by \( \mathrm{R}=\{(x, y): y \) \( =x+5, x \) is a natural number less than \( 4 ; x, y \in \mathrm{N}\} \). Depict this relationship using roster form. Write down the domain and the range.
Answer
Given: \( \mathrm{R}=\{(x, y): y=x+5, x \) is a natural number less than \( 4 ; x, y \in \mathrm{N}\} \).
As \(x\) is a natural number which is less than 4 .
Hence the relation in roaster form, \( \mathrm{R}=\{(1,6),(2,7),(3,8)\} \)
As Domain of \( \mathrm{R}= \) set of all first elements of the order pairs in the relation.
\( \Rightarrow \) Domain of \( \mathrm{R}=\{1,2,3\} \)
Range of \( R= \) set of all second elements of the order pairs in the relation.
\( \Rightarrow \) range of \( R=\{6,7,8\} \).
3. \( \mathrm{~A}=\{1,2,3,5\} \) and \( \mathrm{B}=\{4,6,9\} \). Define a relation \( R \) from \( A \) to \( B \) by \( \mathrm{R}=\{(x, y) \) : the difference between \(x\) and \(y\) is odd; \( x \in \mathrm{A}, y \in \mathrm{B}\} \). Write R in roster form.
Answer
Given: \( \mathrm{A}=\{1,2,3,5\} \) and \( \mathrm{B}=\{4,6,9\} \)
\( \mathrm{R}=\{(x, y) \) : the difference between \( x \) and \( y \) is odd; \( x \in \mathrm{A}, y \in \mathrm{B}\} \)
Now the difference should be odd. Let us take all possible differences. \( (1-4)=-3,(1-6)=-5,(1-9)=-8(2-4)=-2,(2-6)=-4,(2-9)= \) \( -7(3-4)=-1,(3-6)=-3,(3-9)=-6(5-4)=1,(5-6)=-1,(5-9) \) \( =-4 \) Taking the difference which are odd we get,
Hence the relation in roaster form, \( \mathrm{R}=\{(1,4),(1,6),(2,9),(3,4),(3,6) \), \( (5,4),(5,6)\} \)
4. The Fig 2.7 shows a relationship between the sets P and Q . Write this relation
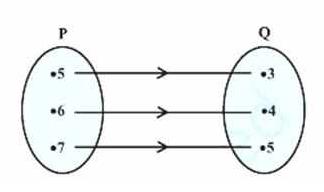
(i) in set-builder form
(ii) roster form.
What is its domain and range?

(i) in set-builder form
(ii) roster form.
What is its domain and range?
Answer
Given:
As we see in given figure: \( \mathrm{P}=\{5,6,7\}, \mathrm{Q}=\{3,4,5\} \)
(i) Hence the relation in set builder form, \( \mathrm{R}=\{(x, y): y=x-2 ; x \in \mathrm{P}\} \) or \( \mathrm{R}=\{(x, y): y=x-2 ; \) for \( x=5,6,7\} \)
(ii) And the relation in roaster form, \( \mathrm{R}=\{(5,3),(6,4),(7,5)\} \)
As Domain of \( \mathrm{R}= \) set of all first elements of the order pairs in the relation.
\( \Rightarrow \) Domain of \( R=\{5,6,7\} \)
Range of \( R= \) set of all second elements of the order pairs in the relation.
\( \Rightarrow \) range of \( R=\{3,4,5\} \).
class 11 ch 2 exercise 2.2 solutions || class 11 maths ncert solutions || ncert solutions for class 11 maths chapter 2 || class 11 maths relations and functions || ncert exemplar class 11 maths || exercise 2.2 class 11 maths solutions || class 11 chapter 2 exercise 2.2 solution
5. Let \( A=\{1,2,3,4,6\} \). Let \( R \) be the relation on \( A \) defined by \( \{(a, b): a, b \in A, b \) is exactly divisible by \( a\} \).
(i) Write R in roster form
(ii) Find the domain of R
(iii) Find the range of R.
(i) Write R in roster form
(ii) Find the domain of R
(iii) Find the range of R.
Answer
Given: \( \mathrm{A}=\{1,2,3,4,6\} \)
\( R=\{(a, b): a, b \in A, b \) is exactly divisible by \( a\} \)
Hence the relation in roaster form, \( R=\{(1,1),(1,2),(1,3),(1,4),(1,6) , (2,2),(2,4),(2,6),(3,3),(3,6),(4,4),(6,6)\} \)
As Domain of \( \mathrm{R}= \) set of all first elements of the order pairs in the relation.
\( \Rightarrow \) Domain of \( \mathrm{R}=\{1,2,3,4,6\} \)
Range of \( \mathrm{R}= \) set of all second elements of the order pairs in the relation.
6. Determine the domain and range of the relation \( R \) defined by
\( \mathrm{R}=\{(x, x+5): x \in\{0,1,2,3,4,5\}\} \).
\( \Rightarrow \) range of \( \mathrm{R}=\{1,2,3,4,6\} \).
\( \mathrm{R}=\{(x, x+5): x \in\{0,1,2,3,4,5\}\} \).
\( \Rightarrow \) range of \( \mathrm{R}=\{1,2,3,4,6\} \).
Answer
Given: \( \mathrm{R}=\{(x, x+5): x \in\{0,1,2,3,4,5\}\} \)
Hence the relation in roaster form, \( \mathrm{R}=\{(0,5),(1,6),(2,7),(3,8),(4,9) \), \( (5,10)\} \)
As Domain of \( \mathrm{R}= \) set of all first elements of the order pairs in the relation.
\( \Rightarrow \) Domain of \( \mathrm{R}=\{0,1,2,3,4,5\} \)
Range of \( \mathrm{R}= \) set of all second elements of the order pairs in the relation.
\( \Rightarrow \) range of \( \mathrm{R}=\{5,6,7,8,9,10\} \).
7. Write the relation \( \mathrm{R}=\left\{\left(x, x_{3}\right)\right. \) : \( x \) is a prime number less than \(10 \} \) in roster form.
Answer
Given: \( \mathrm{R}=\left\{\left(x, x_{3}\right)\right. \) : \(x\) is a prime number less than 10\( \} \)
As we know the prime number less than 10 are 2, 3, 5 and 7 .
Hence the relation in roaster form, \( \mathrm{R}=\{(2,8),(3,27),(5,125),(7 \), 343) \( \} \)
8. Let \( \mathrm{A}=\{x, y, z\} \) and \( \mathrm{B}=\{1,2\} \). Find the number of relations from A to B.
Answer
Given: \( \mathrm{A}=\{x, y, z\} \) and \( \mathrm{B}=\{1,2\} \)
\(\therefore \mathrm{A} \times \mathrm{B}=\{(x, 1),(x, 2),(y, 1),(y, 2),(z, 1),(z, 2)\}\)
\(\Rightarrow \mathrm{n}(\mathrm{A} \times \mathrm{B})=6\)
Then number of subsets of set \( (A \times B)=2 n=26 \)
\( \Rightarrow \) number of relations from A to \( \mathrm{B}=26 \).
9. Let \( R \) be the relation on \( Z \) defined by \( R=\{(a, b): a, b \in Z, a-b \) is an integer \(\}\). Find the domain and range of \(R\).
Answer
Given: \( \mathrm{R}=\{(\mathrm{a}, \mathrm{b}): \mathrm{a}, \mathrm{b} \in \mathrm{Z}, \mathrm{a}-\mathrm{b} \) is an integer \( \} \)
As we know that the difference between any two integers is always an integer.
As Domain of \( \mathrm{R}= \) set of all first elements of the order pairs in the relation.
\( \Rightarrow \) Domain of \( \mathrm{R}=\mathrm{Z} \)
Range of \( R= \) set of all second elements of the order pairs in the relation. \( \Rightarrow \) range of \( \mathrm{R}=\mathrm{Z} \)

