Class 11 Maths Ch 1 Miscellaneous Exercise Solutions

\( A=\{x: x \in R \) and \( x \) satisfies \( x 2-8 x+12=0\} \)
2 and 6 are the only solutions of \( x 2-8 x+12=0 \).
\(\therefore A=\{2,6\}\)
\(B=\{2,4,6\}, C=\{2,4,6,8 \ldots\}, D=\{6\}\)
\(\therefore D \subset A \subset B \subset C\)
Hence, \( \mathrm{A} \subset \mathrm{B}, \mathrm{A} \subset \mathrm{C}, \mathrm{B} \subset \mathrm{C}, \mathrm{D} \subset \mathrm{A}, \mathrm{D} \subset \mathrm{B}, \mathrm{D} \subset \mathrm{C} \)

False
Let \( \mathrm{A}=\{1,2\} \) and \( \mathrm{B}=\{1,\{1,2\},\{3\}\} \)
Now,
\( 2 \in\{1,2\} \) and \( \{1,2\} \in\{\{3\}, 1,\{1,2\}\} \)
\( \therefore \mathrm{A} \in \mathrm{B} \)
However,
\( 2 \notin \{\{3\}, 1\{1,2\}\} \)

False
Let
\( A=\{2\}, B=\{0,2\} \), and \( C=\{1,\{0,2\}, 3\} \)
As \( \mathrm{A} \subset \mathrm{B} \)
\( B \in C \)
However, \( \mathrm{A} \notin \mathrm{C} \)

True
Let \( \mathrm{A} \subset \mathrm{B} \) and \( \mathrm{B} \subset \mathrm{C} \).
Let \( x \in \mathrm{A} \)
\(=x \in \mathrm{B}[\mathrm{A} \subset \mathrm{B}]\)
\(=x \in \mathrm{C}[\mathrm{B} \subset \mathrm{C}]\)
\(\therefore \mathrm{A} \subset \mathrm{C}\)

False
\( A=\{1,2\}, B=\{0,6,8\} \) and \( C=\{0,1,2,6,9\} \)
\( \mathrm{A} \not \subset \mathrm{B} \) and \( \mathrm{B} \not \subset \mathrm{C} \)
Let
Accordingly,
However, \( \mathrm{A} \subset \mathrm{C} \)

False
Let \( \mathrm{A}=\{3,5,7\} \) and \( \mathrm{B}=\{3,4,6\} \)
Now, \( 5 \in \mathrm{A} \) and \( \mathrm{A} \not \subset \mathrm{B} \)
However, \( 5 \notin \mathrm{B} \)

True
Let \( \mathrm{A} \subset \mathrm{B} \) and \( x \notin \mathrm{B} \).
To show: \( x \notin \mathrm{A} \)
If possible, suppose \( x \in A \).
Then, \( x \in B \), which is a contradiction as \( x \notin B \)
\(\therefore x \notin \mathrm{A}\)

Let, \( \mathrm{A}, \mathrm{B} \) and C be the sets such that.
To show: \( \mathrm{B}=\mathrm{C} \)
Let \( x \in \mathrm{B} \)
\(=x \in \mathrm{A} \cup \mathrm{B}[\mathrm{B} \subset \mathrm{A} \cup \mathrm{B}]\)
\(=x \in \mathrm{A} \cup \mathrm{C}[\mathrm{A} \cup \mathrm{B}=\mathrm{A} \cup \mathrm{C}]\)
\(=x \in \mathrm{A} \text { or } x \in \mathrm{C}\)
Case 1 x \( \in \) A
Also, \( x \in B \)
\( \therefore x \in \mathrm{A} \) and \( x \in \mathrm{C} \)
\( \therefore x \in \mathrm{C} \)
\( \therefore \mathrm{B} \subset \mathrm{C} \)
Similarly, we can show that \( \mathrm{C} \subset \mathrm{B} \).
\( \therefore \mathrm{B}=\mathrm{C} \)

First, we have to show that (i) \( \Leftrightarrow \) (ii).
Let \( \mathrm{A} \subset \mathrm{B} \)
To show: \( \mathrm{A}-\mathrm{B} \neq \phi \)
If possible, suppose \( A-B \neq \phi \)
This means that there exists \( x \in A, x \neq B \), which is not possible as \( A \subset \) B.
\( \therefore \mathrm{A}-\mathrm{B}=\phi \)
\( \therefore \mathrm{A} \subset \mathrm{B} \Rightarrow \mathrm{A}-\mathrm{B}=\phi \)
Let \( \mathrm{A}-\mathrm{B}=\phi \)
To show: \( \mathrm{A} \subset \mathrm{B} \)
Let \( x \in \mathrm{A} \)
Clearly, \( x \in B \) because if \( x \notin B \), then \( A-B \neq \phi \)
\( \therefore \mathrm{A}-\mathrm{B}=\phi \Rightarrow \mathrm{A} \subset \mathrm{B} \)
\( \therefore \) (i) \( \Leftrightarrow \) (ii)
Let \( \mathrm{A} \subset \mathrm{B} \)
To show: \( \mathrm{A} \cup \mathrm{B}=\mathrm{B} \)
Clearly, \( \mathrm{B} \subset \mathrm{A} \cup \mathrm{B} \)
Let \( x \in \mathrm{A} \cup \mathrm{B} \)
\( =x \in \mathrm{A} \) or \( x \in \mathrm{B} \)
Case I: \( x \in A \)
\( x \in B[A \subset B] \)
\( A \cup B \subset B \)
Case II: \( x \in B \)
Then, \( \mathrm{A} \cup \mathrm{B}=\mathrm{B} \)
Conversely, let
Let \( x \in \mathrm{A} \)
\( =x \in A \cup B \)
\( =x \in \mathrm{B} \)
\( \mathrm{A} \subset \mathrm{B} \)
Hence, (i) \( \Leftrightarrow \) (iii)
Now, we have to show that (i) \( \Leftrightarrow \) (iv).
Let \( \mathrm{A} \subset \mathrm{B} \)
Clearly
Let \( x \in \mathrm{A} \)
We have to show that
As \( \mathrm{A} \subset \mathrm{B}, x \in \mathrm{B} \)
Hence, \( A=A \cap B \)
Conversely, suppose \( A \cap B=A \)
Let \( x \in \mathrm{A} \)
\(\Rightarrow x \in \mathrm{A} \cap \mathrm{B}\)
\(\Rightarrow x \in \mathrm{A} \text { and } x \in \mathrm{B}\)
\(\Rightarrow x \in \mathrm{B}\)
\(\therefore \mathrm{A} \subset \mathrm{B}\)
Hence, (i) \( \Leftrightarrow \) (iv).

Let \( \mathrm{A} \subset \mathrm{B} \)
To show: \( \mathrm{C}-\mathrm{B} \subset \mathrm{C}-\mathrm{A} \)
Let \( x \in \mathrm{C}-\mathrm{B} \)
\( \Rightarrow x \in \mathrm{C} \) and \( x \notin \mathrm{B} \)
\( \Rightarrow x \in \mathrm{C} \) and \( x \notin \mathrm{A}[\mathrm{A} \subset \mathrm{B}] \)
\( \Rightarrow x \in \mathrm{C}-\mathrm{A} \)
\( \therefore \mathrm{C}-\mathrm{B} \subset \mathrm{C}-\mathrm{A} \)

Let \( \mathrm{P}(\mathrm{A})=\mathrm{P}(\mathrm{B}) \)
To show: \( \mathrm{A}=\mathrm{B} \)
Let \( x \in \mathrm{A} \)
\( \mathrm{A} \in \mathrm{P}(\mathrm{A})=\mathrm{P}(\mathrm{B}) \)
\( \therefore x \in \mathrm{C} \), for some \( \mathrm{C} \in \mathrm{P}(\mathrm{B}) \)
Now, \( \mathrm{C} \subset \mathrm{B} \)
\( \therefore x \in \mathrm{B} \)
\( \therefore \mathrm{A} \subset \mathrm{B} \)
Similarly, B \( \subset \mathrm{A} \)
\( \therefore \mathrm{A}=\mathrm{B} \)

False
Let \( \mathrm{A}=\{0,1\} \) and \( \mathrm{B}=\{1,2\} \)
\(\begin{array}{l}
\therefore A \cup B=\{0,1,2\} \\
P(A)=\{\phi,\{0\},\{1\},\{0,1\}\} \\
P(B)=\{\phi,\{1\},\{2\},\{1,2\}\} \\
P(A \cup B)=\{\phi,\{0\},\{1\},\{2\},\{0,1\},\{1,2\},\{0,2\},\{0,1,2\}\} \\
P(A) \cup P(B)=\{\phi,\{0\},\{1\},\{0,1\},\{2\},\{1,2\}\} \\
\therefore P(A) \cup P(B) \neq P(A \cup B)
\end{array}\)

To show: \( A=(A \cap B) \cup(A-B) \)
Let \( x \in \mathrm{A} \)
We have to show that \( x \in(A \cap B) \cup(A-B) \) Case I \( x \in A \cap B \)
Then, \( x \in(A \cap B) \subset(A \cup B) \cup(A-B) \) Case II \( x \notin A \cap B \)
\( \Rightarrow x \notin \mathrm{A} \) or \( x \notin \mathrm{B} \)
\( \therefore x \notin \mathrm{B}[x \notin \mathrm{A}] \)
\( \therefore x \notin \mathrm{A}-\mathrm{B} \subset(\mathrm{A} \cup \mathrm{B}) \cup(\mathrm{A}-\mathrm{B}) \)
\( \therefore \mathrm{A} \subset(\mathrm{A} \cap \mathrm{B}) \cup(\mathrm{A}-\mathrm{B}) \ldots (1)\)
It is clear that
\( \mathrm{A} \cap \mathrm{B} \subset \mathrm{A} \) and \( (\mathrm{A}-\mathrm{B}) \subset \mathrm{A} \)
\( \therefore(\mathrm{A} \cap \mathrm{B}) \cup(\mathrm{A}-\mathrm{B}) \subset \mathrm{A} \ldots (2)\)
From (1) and (2), we obtain
\(A=(A \cap B) \cup(A-B)\)
To prove: \( \mathrm{A} \cup(\mathrm{B}-\mathrm{A}) \subset \mathrm{A} \cup \mathrm{B} \)
Let \( x \in \mathrm{A} \cup(\mathrm{B}-\mathrm{A}) \)
\(\begin{array}{l}
\Rightarrow x \in A \text { or } x \in(B-A) \\
\Rightarrow x \in A \text { or }(x \in B \text { and } x \notin A) \\
\Rightarrow(x \in A \text { or } x \in B) \text { and }(x \in A \text { or } x \notin A) \\
\Rightarrow x \in(A \cup B) \\
\therefore A \cup(B-A) \subset(A \cup B) \ldots(3)
\end{array}\)
Next, we show that \( (A \cup B) \subset A \cup(B-A) \).
Let \( y \in A \cup B \)
\(\Rightarrow y \in A \text { or } y \in B\)
\(\Rightarrow(y \in A \text { or } y \in B) \text { and }(y \in A \text { or } y \notin A)\)
\(\Rightarrow y \in A \text { or }(y \in B \text { and } y \notin A)\)
\(\Rightarrow y \in A \cup(B-A)\)
\(\therefore A \cup B \subset A \cup(B-A) \ldots(4)\)
Hence, from (3) and (4), we obtain \( A \cup(B-A)=A \cup B \).

To show: \( \mathrm{A} \cup(\mathrm{A} \cap \mathrm{B})=\mathrm{A} \)
We know that
\( \mathrm{A} \subset \mathrm{A} \)
\( \mathrm{A} \cap \mathrm{B} \subset \mathrm{A} \)
\( \therefore \mathrm{A} \cup(\mathrm{A} \cap \mathrm{B}) \subset \mathrm{A} \ldots(1) \)
Also, \( \mathrm{A} \subset \mathrm{A} \cup(\mathrm{A} \cap \mathrm{B}) \ldots(2) \)
\( \therefore \) From (1) and (2), \( \mathrm{A} \cup(\mathrm{A} \cap \mathrm{B})=\mathrm{A} \)

To show: \( \mathrm{A} \cap(\mathrm{A} \cup \mathrm{B})=\mathrm{A} \)
\( A \cap(A \cup B)=(A \cap A) \cup(A \cap B) \)
\( =A \cup(A \cap B) \)
\( =\mathrm{A}\{ \) from \( (1)\} \)

Let \( \mathrm{A}=\{0,1\}, \mathrm{B}=\{0,2,3\} \), and \( \mathrm{C}=\{0,4,5\} \)
Accordingly, \( \mathrm{A} \cap \mathrm{B}=\{0\} \) and \( \mathrm{A} \cap \mathrm{C}=\{0\} \)
Here, \( \mathrm{A} \cap \mathrm{B}=\mathrm{A} \cap \mathrm{C}=\{0\} \)
However, \( \mathrm{B} \neq \mathrm{C}[2 \in \mathrm{B} \) and \( 2 \notin \mathrm{C}] \)

Let \( A \) and \( B \) be two sets such that \( A \cap X=B \cap X=f \) and \( A \cup X=B \cup X\) for
some set X .
To show: \( \mathrm{A}=\mathrm{B} \)
It can be seen that
\(A=A \cap(A \cup X)=A \cap(B \cup X)[A \cup X=B \cup X]\)
\(=(A \cap B) \cup(A \cap X)[\text { Distributive law }]\)
\(=(A \cap B) \cup \phi[A \cap X=\phi]\)
\(=A \cap B \ldots \ldots (1) \)
Now, \( B=B \cap(B \cup X) \)
\(=B \cap(A \cup X)[A \cup X=B \cup X]\)
\(=(B \cap A) \cup(B \cap X) \text { [Distributive law] }\)
\(=(B \cap A) \cup \phi[B \cap X=\phi]\)
\(=\mathrm{B} \cap \mathrm{A}\)
\(=A \cap B \ldots \ldots (2) \)
Hence, from (1) and (2), we obtain \( \mathrm{A}=\mathrm{B} \).

Let \( A=\{0,1\}, B=\{1,2\} \), and \( C=\{2,0\} \).
Accordingly, \( \mathrm{A} \cap \mathrm{B}=\{1\}, \mathrm{B} \cap \mathrm{C}=\{2\} \), and \( \mathrm{A} \cap \mathrm{C}=\{0\} \).
\( \therefore \mathrm{A} \cap \mathrm{B}, \mathrm{B} \cap \mathrm{C} \), and \( \mathrm{A} \cap \mathrm{C} \) are non-empty.
However, \( \mathrm{A} \cap \mathrm{B} \cap \mathrm{C}=\phi \)

Let \( U \) be the set of all students who took part in the survey.
Let T be the set of students taking tea.
Let C be the set of students taking coffee.
Accordingly, \( \mathrm{n}(\mathrm{U})=600, \mathrm{n}(\mathrm{T})=150, \mathrm{n}(\mathrm{C})=225, \mathrm{n}(\mathrm{T} \cap \mathrm{C})=100 \)
To find: Number of student taking neither tea nor coffee i.e., we have to find \( n\left(T^{\prime} \cap C^{\prime}\right) \).
\(\begin{array}{l}
n\left(T^{\prime} \cap C^{\prime}\right)=n(T \cup C)^{\prime} \\
=n(U)-n(T \cup C) \\
=n(U)-[n(T)+n(C)-n(T \cap C)] \\
=600-[150+225-100] \\
=600-275 \\
=325
\end{array}\)
Hence, 325 students were taking neither tea nor coffee.

Let \( U \) be the set of all students in the group.
Let \( E \) be the set of all students who know English.
Let H be the set of all students who know Hindi.
\( \therefore \mathrm{H} \cup \mathrm{E}=\mathrm{U} \)
Accordingly, \( \mathrm{n}(\mathrm{H})=100 \) and \( \mathrm{n}(\mathrm{E})=50 \)
\( n(H \cup E)=n(H)+n(E)-n(H \cap E) \)
\( =100+50-25 \)
\( =125 \)
Hence, there are 125 students in the group.

Let \( A \) be the set of people who read newspaper H. Let B be the set of people
who read newspaper T. Let C be the set of people who read newspaper I.
Accordingly,
\(n(A)=25, n(B)=26, n(C)=26, n(A \cap C)=9, n(A \cap B)=11\)
\(n(B \cap C)=8, n(A \cap B \cap C)=3\)
Let \( U \) be the set of people who took part in the survey.
(i) Accordingly,
\( \mathrm{n}(\mathrm{A} \mathrm{B} \mathrm{C})=\mathrm{n}(\mathrm{A})+\mathrm{n}(\mathrm{B})+\mathrm{n}(\mathrm{C})-\mathrm{n}(\mathrm{A} \cap \mathrm{B})-\mathrm{n}(\mathrm{B} \cap \mathrm{C})-\mathrm{n}(\mathrm{C} \cap \mathrm{A})+ \) \( \mathrm{n}(\mathrm{A} \cap \mathrm{B} \cap \mathrm{C})=25+26+26-11-8-9+3=52 \)
Hence, 52 people read at least one of the newspapers.
(ii) Let a be the number of people who read newspapers H and T only.

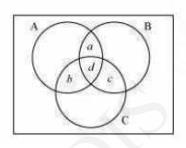
Let b denote the number of people who read newspapers I and H only.
Let c denote the number of people who read newspapers T and I only.
Let \( d \) denote the number of people who read all three newspapers.
Accordingly, \( d=n(A \cap B \cap C)=3 \)
Now, \( n(A \cap B)=a+d \)
\( \mathrm{n}(\mathrm{B} \cap \mathrm{C})=\mathrm{c}+\mathrm{d} \)
\( \mathrm{n}(\mathrm{C} \cap \mathrm{A})=\mathrm{b}+\mathrm{d} \)
\(\therefore \mathrm{a}+\mathrm{d}+\mathrm{c}+\mathrm{d}+\mathrm{b}+\mathrm{d}=11+8+9=28\)
\(\Rightarrow \mathrm{a}+\mathrm{b}+\mathrm{c}+\mathrm{d}=28-2 \mathrm{~d}=28-6=22\)
Hence, \( (52-22)=30 \) people read exactly one newspaper.

Let \( \mathrm{A}, \mathrm{B} \), and C be the set of people who like product A , product B , and productC respectively.
Accordingly, \( \mathrm{n}(\mathrm{A})=21, \mathrm{n}(\mathrm{B})=26, \mathrm{n}(\mathrm{C})=29, \mathrm{n}(\mathrm{A} \cap \mathrm{B})=14, \mathrm{n}(\mathrm{C} \cap \mathrm{A})=12, \)
\(\mathrm{n}(\mathrm{B} \cap \mathrm{C})=14, \mathrm{n}(\mathrm{A} \cap \mathrm{B} \cap \mathrm{C})=8 \)
The Venn diagram for the given problem can be drawn as

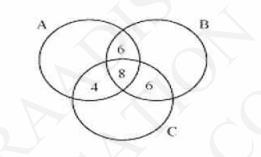
It can be seen that number of people who like product C only is \( \{29-(4+8+6)\}=11 \)