Class 11 Maths Chapter 1 Exercise 1.5 Solutions

Class 11 maths chapter 1 exercise 1.5 solutions | exercise 1.5 class 11 maths | class 11 ch 1 exercise solutions | class 11 chapter 1 exercise solution | sets class 11 ncert solutions | ncert solution for class 11 maths chapter 1 | ncert exemplar class 11 maths

Looking for NCERT Class 11 Maths Exercise 1.5 solutions? You’re in the right place! This section offers detailed and easy-to-understand solutions for all the questions from Exercise 1.5 of Chapter 1 – Sets. Based on the latest NCERT syllabus, these solutions focus on practical problems involving union and intersection of sets using Venn diagrams and real-life contexts. Whether you’re revising for exams or aiming to clear your fundamentals, these Class 11 Maths Chapter 1 solutions will guide you every step of the way. View or download the complete solutions now and master the concept of sets with ease!

exercise 1.5 class 11 maths || sets class 11 ncert solutions || ncert solution for class 11 maths chapter 1 || class 11 maths chapter 1 exercise 1.5 solutions || ncert exemplar class 11 maths || class 11 ch 1 exercise solutions || class 11 chapter 1 exercise solution

Download the Math Ninja App Now

Exercise 1.5

1. Let $ U=\{1,2,3,4,5,6,7,8,9\}, A=\{1,2,3,4\}, B=\{2,4,6,8\} $ and $ \mathrm{C}=\{3,4,5,6\} $. Find
(i) A' (ii) B' (iii) $ (\mathrm{A} \cup \mathrm{C})^{\prime} $ (iv) $ (\mathrm{A} \cup \mathrm{B})^{\prime} $ (v) (A')' (vi) $ (\mathrm{B}-\mathrm{C})^{\prime} $

Answer

$ U=\{1,2,3,4,5,6,7,8,9\} A=\{1,2,3,4\} B=\{2,4,6,8\} $
$ \mathrm{C}=\{3,4,5,6\} $
(i) $ \mathrm{A}^{\prime}=\{5,6,7,8,9\} $
(ii) $ \mathrm{B}^{\prime}=\{1,3,5,7,9\} $
(iii) $ \mathrm{A} \cup \mathrm{C}=\{1,2,3,4,5,6\} $
$=(A \cup C)^{\prime}=\{7,8,9\}$
(iv) $ \mathrm{A} \cup \mathrm{B}=\{1,2,3,4,6,8\} $
$ (A \cup B)^{\prime}=\{5,7,9\} $
(v) $ \left(\mathrm{A}^{\prime}\right)^{\prime}=\mathrm{A}=\{1,2,3,4\} $
(vi) $ \mathrm{B}-\mathrm{C}=\{2,8\} $
$(B-C)^{\prime}=\{1,3,4,5,6,7,9\}$

2. If $ U=\{a, b, c, d, e, f, g, h\} $, find the complements of the following sets:
(i) $ \mathrm{A}=\{\mathrm{a}, \mathrm{b}, \mathrm{c}\} $ (ii) $ B=\{d, e, f, g\} $ (iii) $ \mathrm{C}=\{\mathrm{a}, \mathrm{c}, \mathrm{e}, \mathrm{g}\} $ (iv) $ D=\{f, g, h, a\} $

Answer

$ \mathrm{U}=\{\mathrm{a}, \mathrm{b}, \mathrm{c}, \mathrm{d}, \mathrm{e}, \mathrm{f}, \mathrm{g}, \mathrm{h}\} $
(i) $ \mathrm{A}=\{\mathrm{a}, \mathrm{b}, \mathrm{c}\} $
$ A^{\prime}=\{d, e, f, g, h\} $
(ii) $ B=\{d, e, f, g\} $
$ B^{\prime}=\{a, b, c, h\} $
(iii) $ \mathrm{C}=\{\mathrm{a}, \mathrm{c}, \mathrm{e}, \mathrm{g}\} $
$ C^{\prime}=\{b, d, f, h\} $
(iv) $ D=\{\mathrm{f}, \mathrm{g}, \mathrm{h}, \mathrm{a}\} $
$ D^{\prime}=\{b, c, d, e\} $

3. Taking the set of natural numbers as the universal set, write down the complements of the following sets:

exercise 1.5 class 11 maths || sets class 11 ncert solutions || ncert solution for class 11 maths chapter 1 || class 11 maths chapter 1 exercise 1.5 solutions || ncert exemplar class 11 maths || class 11 ch 1 exercise solutions || class 11 chapter 1 exercise solution

Download the Math Ninja App Now

(i) $ \{x: x $ is an even natural number}

Answer

$ \mathrm{U}=\mathrm{N} $ : Set of natural numbers
$ \{x: x \text { is an even natural number }\}^{\prime}=\{x: x $ is an odd natural number $ \} $

(ii) $ \{x: x $ is an odd natural number}

Answer

$ \mathrm{U}=\mathrm{N} $ : Set of natural numbers
$ \{x: x \text { is an odd natural number }\}^{\prime}=\{x: x $ is an even natural number $ \} $

(iii) $ \{x: x $ is a positive multiple of 3}

Answer

$ \mathrm{U}=\mathrm{N} $ : Set of natural numbers
$ \{x \text { : } x \text { is a positive multiple of } 3\}^{\prime}=\{x: x\ N $ and x is not a multiple of $ 3\} $

(iv) $ \{x: x $ is a prime number}

Answer

$ \mathrm{U}=\mathrm{N} $ : Set of natural numbers
$ \{x: x \text { is a prime number }\}^{\prime}=\{x: x $ is a positive composite number and $ x=1\} $

exercise 1.5 class 11 maths || sets class 11 ncert solutions || ncert solution for class 11 maths chapter 1 || class 11 maths chapter 1 exercise 1.5 solutions || ncert exemplar class 11 maths || class 11 ch 1 exercise solutions || class 11 chapter 1 exercise solution

Download the Math Ninja App Now

$Mathninja.in$

(v) {x: x is a natural number divisible by 3 and 5}

Answer

$ \mathrm{U}=\mathrm{N} $ : Set of natural numbers
$ \{x \text { : } x \text { is a natural number divisible by } 3 \text { and } 5\}^{\prime}=\{x: x $ is a natural number that is not divisible by 3 or 5$ \} $

(vi) $ \{x: x $ is a perfect square}

Answer

$ \mathrm{U}=\mathrm{N} $ : Set of natural numbers
$ \{x \text { : } x \text { is a perfect square }\}^{\prime}=\{x: x\ N $ and x is not a perfect square $ \} $

(vii) $ \{x: x $ is a perfect cube}

Answer

$ \mathrm{U}=\mathrm{N} $ : Set of natural numbers
$ \{x: x \text { is a perfect cube }\}^{\prime}=\{x: x \ N $ and x is not a perfect cube $ \} $

(viii) $ \{x: x+5=8\} $

Answer

$ \mathrm{U}=\mathrm{N} $ : Set of natural numbers
$ \{x: x+5=8\}^{\prime}=\{x: x \ N $ and $ x \neq 3\} $

exercise 1.5 class 11 maths || sets class 11 ncert solutions || ncert solution for class 11 maths chapter 1 || class 11 maths chapter 1 exercise 1.5 solutions || ncert exemplar class 11 maths || class 11 ch 1 exercise solutions || class 11 chapter 1 exercise solution

Download the Math Ninja App Now

(ix) $ \{x: 2 x+5=9\} $

Answer

$ \mathrm{U}=\mathrm{N} $ : Set of natural numbers
$ \{x: 2 x+5=9\}^{\prime}=\{x: x $ N and $ x \neq 2\} $

(x) $ \{x: x \geq 7\} $

Answer

$ \mathrm{U}=\mathrm{N} $ : Set of natural numbers
$ \{x: x \geq 7\}^{\prime}=\{x: x $ N and $ x < 7\} $

(xi) $ \{x: x \in \mathrm{N} $ and 2x + 1 > 10}

Answer

$ \mathrm{U}=\mathrm{N} $ : Set of natural numbers
$ \{x: x \ \mathrm{N} \text { and } 2 x+1 > 10\}^{\prime}=\{x: x \ \mathrm{N} $ and $ x \leq \frac{ 9 }{ 2 }\} $

4. If $ U=\{1,2,3,4,5,6,7,8,9\}, A=\{2,4,6,8\} $ and $ B=\{2,3,5 $, $ 7\} $.
Verify that (i) $ (A \cup B)^{\prime}=A^{\prime} \cap B^{\prime} $ (ii) $ (A \cap B)^{\prime}=A^{\prime} \cup B^{\prime} $

Answer

$\mathrm{U}=\{1,2,3,4,5,6,7,8,9\}$
$\mathrm{A}=\{2,4,6,8\}, B=\{2,3,5,7\}$
(i) $(A \cup B)^{\prime}=\{2,3,4,5,6,7,8\}^{\prime}=\{1,9\}$
$A^{\prime} \cap B^{\prime}=\{1,3,5,7,9\} \cap(1,4,6,8,9)=\{1,9\}$
$=(A \cup B)^{\prime}=A^{\prime} \cap B^{\prime}$
(ii) $ (\mathrm{A} \cap \mathrm{B})^{\prime}=\{2\}^{\prime}=\{1,3,4,5,6,7,8,9\} $
$ A^{\prime} \cup B^{\prime}=\{1,3,5,7,9\} \cup\{1,4,6,8,9\}=\{1,3,4,5,6,7,8,9\} $ $ =(A \cap B)^{\prime}=A^{\prime} \cup B^{\prime} $

5. Draw appropriate Venn diagram for each of the following:

(i) $ (\mathrm{A} \cup \mathrm{B})^{\prime} $,

Answer

Yellow region is ( $ \mathrm{A} \cup \mathrm{B} $ ).

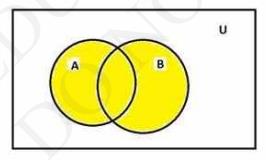
The shaded region represents $ (A \cup B) $.
We have to draw diagram for complement of $ (A \cup B) $ i.e., $ (A \cup B)^{\prime} $, which is given by $ U-(A \cup B) $.
Green region is $ (\mathrm{A} \cup \mathrm{B})^{\prime} $.

(ii) $\mathrm{A}^{\prime} \cap \mathrm{B}^{\prime}$,

Answer

A' $ \cap $ B'
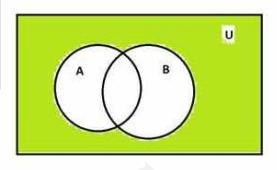
Here we have to draw diagram of $ \left(A^{\prime} \cap B^{\prime}\right) $
So, first we draw $ A^{\prime}=(U-A) $

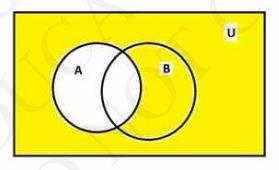
Now, we draw B' (= U - B)

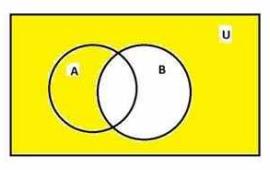
Now the area common in both the shaded regions gives us ( $ \mathrm{A}^{\prime} \cap \mathrm{B}^{\prime} $ )

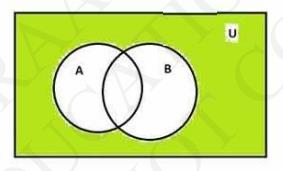
Here, we observe that the final result for (i) and (ii) is same.
$\Rightarrow(\mathrm{A} \cup \mathrm{B})^{\prime}=\left(\mathrm{A}^{\prime} \cap \mathrm{B}^{\prime}\right)$

(iii) $ (\mathrm{A} \cap \mathrm{B})^{\prime} $,

Answer

$ (\mathrm{A} \cap \mathrm{B})^{\prime} $
First we draw $ (\mathrm{A} \cap \mathrm{B}) $

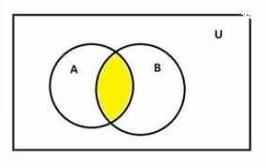
The shaded region represents $ (A \cap B) $.
We have to draw diagram for complement of $ (A \cap B) $ i.e., $ (A \cap B)^{\prime} $, which is given by $ U-(A \cap B) $

(iv) $\mathrm{A}^{\prime} \cup \mathrm{B}^{\prime}$

Answer

$\mathrm{A}^{\prime} \cup \mathrm{B}^{\prime}$
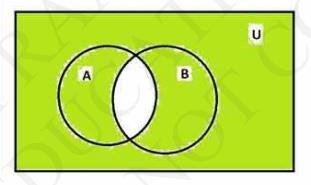
Here we have to draw diagram of ( $ A^{\prime} \cup B^{\prime} $ )
So, first we draw $ A^{\prime}=(U-A) $

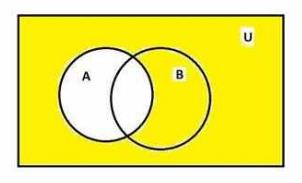
Now, we draw B' (= U - B)

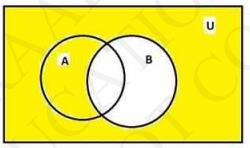
Now the area present in both is added to give ( $\mathrm{A}^{\prime} \cup \mathrm{B}^{\prime}$)

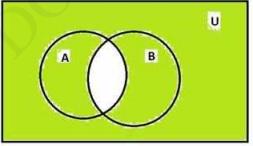
Here, we observe that the final result for (iii) and (iv) is same.
$\Rightarrow(\mathrm{A} \cap \mathrm{B})^{\prime}=\left(\mathrm{A}^{\prime} \cup \mathrm{B}^{\prime}\right)$

6. Let $ U $ be the set of all triangles in a plane. If $ A $ is the set of all triangles with at least one angle different from $ 60^{\circ} $, what is $ \mathrm{A}^{\prime} $ ?

Answer

A" = is the set of all equilateral triangles.

7. Fill in the blanks to make each of the following a true statement:
(i) $ \mathrm{A} \cup \mathrm{A}^{\prime}= \ldots$ (ii) $ \phi^{\prime} \cap \mathrm{A}= \ldots$ (iii) $ \mathrm{A} \cap \mathrm{A}^{\prime}= \ldots$ (iv) $ U^{\prime} \cap A= \ldots$

Answer

(i) $ \mathrm{A} \cup \mathrm{A}^{\prime}=\mathrm{U} $
(ii) $ \phi^{\prime} \cap \mathrm{A}=\mathrm{U} \cap \mathrm{A}=\mathrm{A} $
$ \therefore \phi^{\prime} \cap \mathrm{A}=\mathrm{A} $
(iii) $ \mathrm{A} \cap \mathrm{A}^{\prime}=\phi $
(iv) $ \mathrm{U}^{\prime} \cap \mathrm{A}=\phi \cap \mathrm{A}=\phi $
$ \therefore \mathrm{U}^{\prime} \cap \mathrm{A}=\phi $

exercise 1.5 class 11 maths || sets class 11 ncert solutions || ncert solution for class 11 maths chapter 1 || class 11 maths chapter 1 exercise 1.5 solutions || ncert exemplar class 11 maths || class 11 ch 1 exercise solutions || class 11 chapter 1 exercise solution

Download the Math Ninja App Now