Class 11 maths exercise 6.2 solutions | exercise 6.2 class 11 maths solutions | class 11 ch 6 exercise 6.2 solutions | class 11 chapter 6 exercise 6.2 solution | class 11 maths ncert solutions chapter 6 | ncert solutions for class 11 maths chapter 6 | ncert exemplar class 11 maths | linear inequalities class 11 ncert solutions
Looking for Class 11 Maths Exercise 6.2 solutions? You’re at the right place! This section offers detailed and accurate solutions to all the questions from Exercise 6.2 of Chapter 6 – Linear Inequalities. These solutions follow the latest NCERT syllabus and cover the concepts of linear inequalities in two variables, graphical representation of solutions, and related problem-solving techniques. Whether you’re studying from the Class 11 Ch 6 Exercise 6.2 solutions or referring to the NCERT Exemplar Class 11 Maths, these step-by-step explanations will help you build a solid foundation. Download or explore the Class 11 Maths NCERT Solutions Chapter 6 now and strengthen your command over linear inequalities Class 11!

class 11 chapter 6 exercise 6.2 solution || ncert solutions for class 11 maths chapter 6 || linear inequalities class 11 ncert solutions || exercise 6.2 class 11 maths solutions || class 11 maths ncert solutions chapter 6 || class 11 maths exercise 6.2 solutions || class 11 ch 6 exercise 6.2 solutions || ncert exemplar class 11 maths
Exercise 6.2
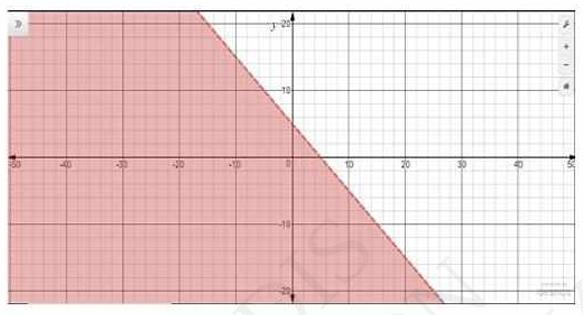
1. Solve the following inequalities graphically in two-dimensional plane: \(x+y < 5\)
Answer
\(\begin{array}{|l|l|l|}
\hline x & 0 & 5 \\
\hline y & 5 & 0 \\
\hline
\end{array}\)
The graphical representation of \( x+y=5 \) is given as dotted line in the figure below. This line divides the \( {x} y \) - plane in two half planes I and II.
Select a point (not on the line). Which lies in one of the half planes, to determine whether the point satisfies the given inequality or not.
We select the point as \( (0,0) \)
It is observed that,
\((0) +0 < 5 \) or \( 0 \geq 5 \) which is true
Therefore, lower half plane II is not the solution region of the given inequality. Also, it is evident that any point on the line satisfies the given inequality.
Thus, the solution region of the given inequality is the half plane I including the line.
The solution region is represented by the shaded region as follow.
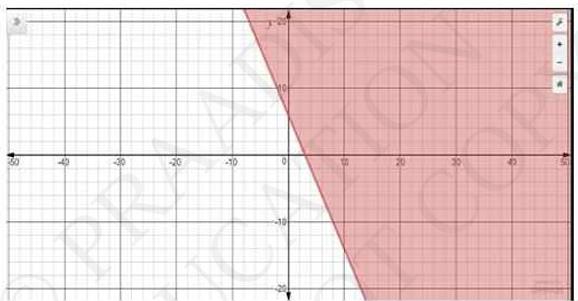
2. Solve the following inequalities graphically in two-dimensional plane: \(2 x+y \geq 6\)
Answer
\(\begin{array}{|l|l|l|}
\hline x & 0 & 3 \\
\hline y & 6 & 0 \\
\hline
\end{array}\)
The graphical representation of \( 2 {x}+{y}=6 \) is given as dotted line in the figure below. This line divides the \(x y\) - plane in two half planes I and II.
Select a point (not on the line). Which lies in one of the half planes, to determine whether the point satisfies the given inequality or not.
We select the point as \( (0,0) \)
It is observed that,
\( 2(0)+0 \geq 6 \) or \( 0 \geq 6 \) which is true
Therefore, lower half plane I is not the solution region of the given inequality. Also, it is evident that any point on the line satisfies the given inequality.
Thus, the solution region of the given inequality is the half plane II including the line.
The solution region is represented by the shaded region as follow.
class 11 chapter 6 exercise 6.2 solution || ncert solutions for class 11 maths chapter 6 || linear inequalities class 11 ncert solutions || exercise 6.2 class 11 maths solutions || class 11 maths ncert solutions chapter 6 || class 11 maths exercise 6.2 solutions || class 11 ch 6 exercise 6.2 solutions || ncert exemplar class 11 maths
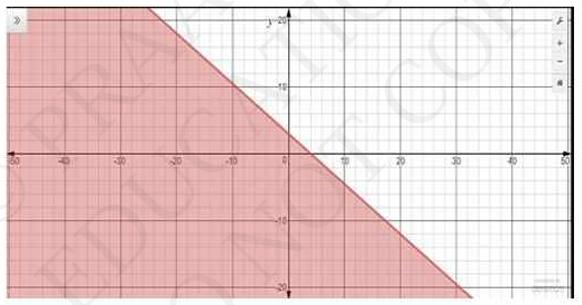
3. Solve the following inequalities graphically in two-dimensional plane: \(3 x+4 y \leq 12\)
Answer
\(\begin{array}{|l|l|l|}
\hline x & 0 & 4 \\
\hline y & 3 & 0 \\
\hline
\end{array}\)
\(3 x+4 y \leq 12\)
The graphical represented of \( 3 x+4 y=12 \) is given in the figure below.
This line divides the \(x y\) - plane in two half planes, I and II.
Select a point (not on the line), which lies in one of the half planes, to determines the point satisfies the given inequality or not.
We select the point as \( (0,0) \)
Thus, the solution region of the given inequality is the shaded half plane I including the point on the line.
This can be represented as follow.
4. Solve the following inequalities graphically in two-dimensional plane: \(y+8 \geq 2 x\)
Answer
\(\begin{array}{|l|l|l|}
\hline x & 0 & 4 \\
\hline y & -8 & 0 \\
\hline
\end{array}\)
The graphical representation of \( {y}+8=2 {x} \) is given as dotted line in the figure below. This line divides the \(x y\) - plane in two half planes.
Select a point (not on the line). Which lies in one of the half planes, to determine whether the point satisfies the given inequality or not.
We select the point as \( (0,0) \)
It is observed that,
\( 0+8 \leq 2 \) or \( 8 \geq 2 \) which is true
Therefore, lower half plane is not the solution region of the given inequality. Also, it is evident that any point on the line satisfies the given inequality.
Thus, the solution region of the given inequality is the half plane containing the point \( (0,0) \) including the line.
The solution region is represented by the shaded region as follow.

class 11 chapter 6 exercise 6.2 solution || ncert solutions for class 11 maths chapter 6 || linear inequalities class 11 ncert solutions || exercise 6.2 class 11 maths solutions || class 11 maths ncert solutions chapter 6 || class 11 maths exercise 6.2 solutions || class 11 ch 6 exercise 6.2 solutions || ncert exemplar class 11 maths
5. Solve the following inequalities graphically in two-dimensional plane: \(x-y \leq 2\)
Answer
\(\begin{array}{|l|l|l|}
\hline x & 0 & 2 \\
\hline y & -2 & 0 \\
\hline
\end{array}\)
The graphical representation of \( {x}-{y}=2 \) is given as dotted line in the figure below. This line divides the \(x y\) - plane in two half planes.
Select a point (not on the line). Which lies in one of the half planes, to determine whether the point satisfies the given inequality or not.
We select the point as \( (0,0) \)
It is observed that,
\( 0-0 \leq 2 \) or \( 0 > 2 \) which is true
Therefore, lower half plane is not the solution region of the given inequality. Also, it is evident that any point on the line satisfies the given inequality.
Thus, the solution region of the given inequality is the half plane containing the point \( (0,0) \) including the line.
The solution region is represented by the shaded region as follow.
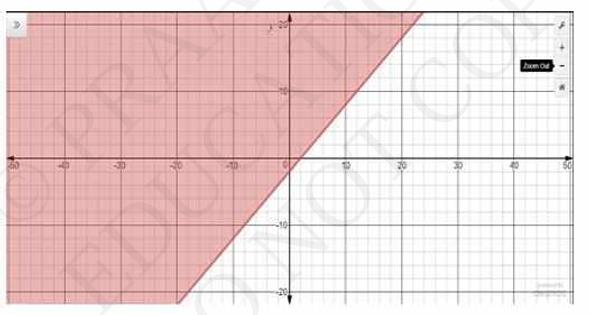
6. Solve the following inequalities graphically in two-dimensional plane: \(2 x-3 y > 6\)
Answer
\(\begin{array}{|l|l|l|}
\hline x & 0 & 3 \\
\hline y & -2 & 0 \\
\hline
\end{array}\)
The graphical representation of \( 2 x-3 y=6 \) is given as dotted line in the figure below. This line divides the \(x y\) - plane in two half planes.
Select a point (not on the line). Which lies in one of the half planes, to determine whether the point satisfies the given inequality or not.
We select the point as \( (0,0) \)
It is observed that,
\( 2(0)-3(0) > 6 \) or \( 0 < 6 \) which is true
Therefore, upper half plane is not the solution region of the given inequality. Also, it is evident that any point on the line satisfies the given inequality.
Thus, the solution region of the given inequality is the half plane does not contain the point \( (0,0) \) including the line.
The solution region is represented by the shaded region as follow
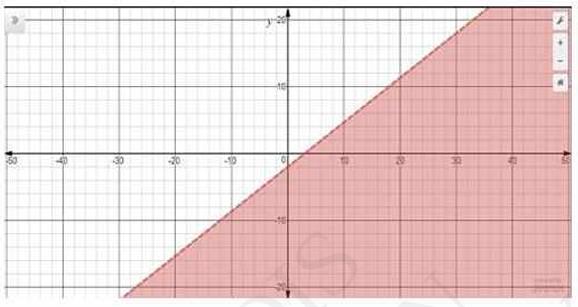
7. Solve the following inequalities graphically in two-dimensional plane: \( -3 x+2 y \geq-6 \)
Answer
\(\begin{array}{|l|l|l|}
\hline x & 0 & 2 \\
\hline y & -3 & 0 \\
\hline
\end{array}\)
The graphical representation of \( -3 x+2 y=-6 \) is given as dotted line in the figure below. This line divides the \(x y\) -plane in two half planes.
Select a point (not on the line). Which lies in one of the half planes, to determine whether the point satisfies the given inequality or not.
We select the point as \( (0,0) \)
It is observed that,
\( -3(0)+2(0) \geq-6 \) or \( 0 > -6 \) which is true
Therefore, lower half plane is not the solution region of the given inequality. Also, it is evident that any point on the line satisfies the given inequality.
Thus, the solution region of the given inequality is the half plane containing the point \( (0,0) \) including the line.
The solution region is represented by the shaded region as follow.
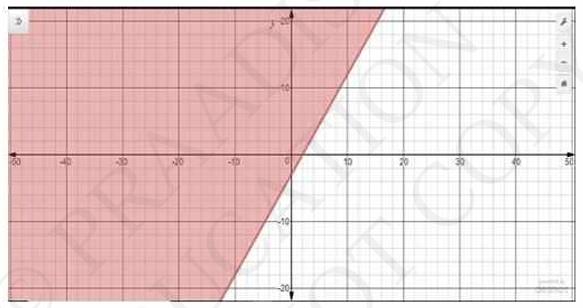
8. Solve the following inequalities graphically in two-dimensional plane: \(3 y-5 x < 30\)
Answer
\(\begin{array}{|l|l|l|}
\hline x & 0 & -6 \\
\hline y & 10 & 0 \\
\hline
\end{array}\)
The graphical representation of \( 3 y-5 x < 30 \) is given as dotted line in the figure below. This line divides the \( {x} y- \) plane in two half planes.
Select a point (not on the line). Which lies in one of the half planes, to determine whether the point satisfies the given inequality or not.
We select the point as \( (0,0) \)
It is observed that,
\( 3(0)-5(0) < 30 \) or \( 0 > 30 \) which is true
Also, it is evident that any point on the line does not satisfies the given inequalities.
Therefore, the upper half plane is not the solutions region of the given inequality. Also, it is evident that any point on the line does not satisfy the given inequality.
Thus, the solution region of the given inequality is the half plane containing the point \( (0,0) \) including the line.
The solution region is represented by the shaded region as follow.
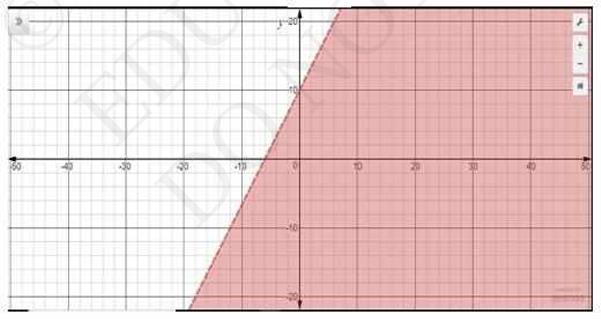
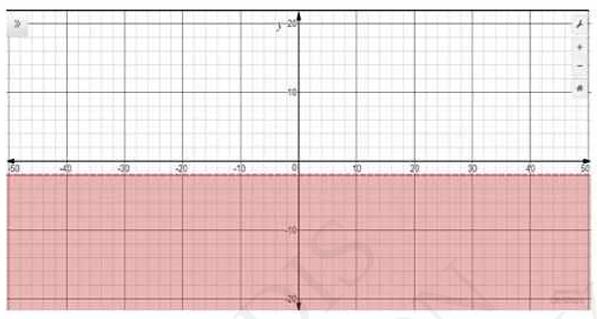
9. Solve the following inequalities graphically in two-dimensional plane: \(y < -2\)
Answer
The graphical representation of \( y=-2 \) is given as dotted line in the figure below. This line divides the \(x y\) - plane in two half planes.
Select a point (not on the line). Which lies in one of the half planes, to determine whether the point satisfies the given inequality or not.
We select the point as \( (0,0) \)
It is observed that,
\( 0 < -2 \), which is true
Also, it is evident that any point on the line does not satisfies the given inequalities.
Hence, every point on the right side of the line, \( y=-2 \) (excluding all the points on the line), determines the solutions of the given inequalities.
The solutions regions are represented by the shaded region as follow.
The graph is as follows:
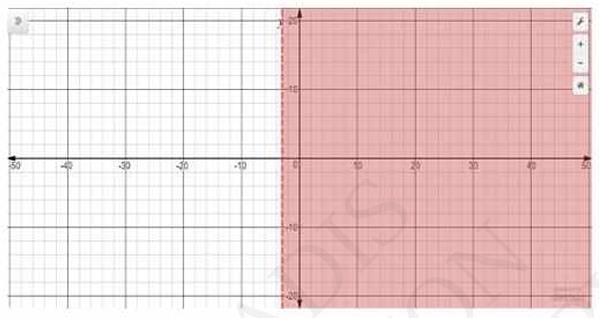
10. Solve the following inequalities graphically in two-dimensional plane: \(x > -3\)
Answer
The graphical representation of \( x=-3 \) is given as dotted line in the figure below. This line divides the \(x y\) - plane in two half planes.
Select a point (not on the line). Which lies in one of the half planes, to determine whether the point satisfies the given inequality or not.
We select the point as \( (0,0) \)
It is observed that,
\( 0-3 \), which is true
Also, it is evident that any point on the line does not satisfies the given inequalities.
Hence, every point on the right side of the line, \( x=3 \) (excluding all the points on the line), determines the solutions of the given inequalities.
The solutions regions are represented by the shaded region as follow.