Class 12 maths chapter 9 miscellaneous exercise solutions | miscellaneous exercise chapter 9 class 12 | miscellaneous exercise class 12 chapter 9 | differential equations class 12 ncert solutions
Get complete and reliable Class 12 Maths Chapter 9 Miscellaneous Exercise Solutions to strengthen your understanding of Differential Equations. The Miscellaneous Exercise Chapter 9 Class 12 combines all major concepts from the chapter, offering a mix of challenging and conceptual questions. Our step-by-step explanations in the Miscellaneous Exercise Class 12 Chapter 9 help students revise and apply different methods such as variable separable, homogeneous equations, and linear differential equations. These well-organized Differential Equations Class 12 NCERT Solutions are ideal for board exam preparation and concept clarity.

miscellaneous exercise chapter 9 class 12 || differential equations class 12 ncert solutions || miscellaneous exercise class 12 chapter 9 || class 12 maths chapter 9 miscellaneous exercise solutions
Miscellaneous Exercise
1A. For each of the differential equations given below, indicate its order and degree (if defined).
\(\frac{d^{2} y}{d x^{2}}+5 x\left(\frac{d y}{d x}\right)^{2}-6 y=\log x\)
\(\frac{d^{2} y}{d x^{2}}+5 x\left(\frac{d y}{d x}\right)^{2}-6 y=\log x\)
Answer
It is given that equation is \( \frac{d^{2} y}{d x^{2}}+5 x\left(\frac{d y}{d x}\right)^{2}-6 y=\log x \)
\(\frac{d^{2} y}{d x^{2}}+5 x\left(\frac{d y}{d x}\right)^{2}-6 y-\log x=0\)
We can see that the highest order derivative present in the differential is \( \frac{d^{2} y}{d x^{2}} \).
Thus, its order is two. It is polynomial equation in \( \frac{d^{2} y}{d x^{2}} \). The highest power raised to \( \frac{d^{2} y}{d x^{2}} \) is \(1 \).
Therefore, its degree is one.
1B. For each of the differential equations given below, indicate its order and degree (if defined).
\(\left(\frac{d y}{d x}\right)^{3}-4\left(\frac{d y}{d x}\right)^{2}+7 y=\sin x\)
\(\left(\frac{d y}{d x}\right)^{3}-4\left(\frac{d y}{d x}\right)^{2}+7 y=\sin x\)
Answer
It is given that equation is \( \left(\frac{d y}{d x}\right)^{3}-4\left(\frac{d y}{d x}\right)^{2}+7 y=\sin x \)
\(\left(\frac{d y}{d x}\right)^{3}-4\left(\frac{d y}{d x}\right)^{2}+7 y-\sin x=0\)
We can see that the highest order derivative present in the differential is \( \frac{d y}{d x} \).
Thus, its order is one. It is polynomial equation in \( \frac{d y}{d x} \) The highest power raised to \( \frac{d y}{d x} \) is \(3 \).
Therefore, its degree is three.
1C. For each of the differential equations given below, indicate its order and degree (if defined).
\(\frac{d^{4} y}{d x^{4}}-\sin \left(\frac{d^{3} y}{d x^{3}}\right)=0\)
\(\frac{d^{4} y}{d x^{4}}-\sin \left(\frac{d^{3} y}{d x^{3}}\right)=0\)
Answer
It is given that equation is \( \frac{d^{4} y}{d x^{4}}-\sin \left(\frac{d^{3} y}{d x^{3}}\right)=0 \)
\(\frac{d^{2} y}{d x^{2}}+5 x\left(\frac{d y}{d x}\right)^{2}-6 y-\log x=0\)
We can see that the highest order derivative present in the differential is \( \frac{d^{4} y}{d x^{4}} \).
Thus, its order is four. The given differential equation is not a polynomial equation.
Therefore, its degree is not defined.
miscellaneous exercise chapter 9 class 12 || differential equations class 12 ncert solutions || miscellaneous exercise class 12 chapter 9 || class 12 maths chapter 9 miscellaneous exercise solutions
2A. For each of the exercises given below, verify that the given function (implicit or explicit) is a solution of the corresponding differential equation.
\(x y=a e^{x}+b e^{-x}+x^{2} ; x \frac{d^{2} y}{d x^{2}}+2 \frac{d y}{d x}-x y+x^{2}-2=0\)
\(x y=a e^{x}+b e^{-x}+x^{2} ; x \frac{d^{2} y}{d x^{2}}+2 \frac{d y}{d x}-x y+x^{2}-2=0\)
Answer
It is given that \( x y=a e^{x}+b e^{-x}+x^{2} \)
Now, differentiating both sides w.r.t. \(x\), we get,
\(\frac{d y}{d x}=a \frac{d}{d x}\left(e^{x}\right)+b \frac{d}{d x}\left(e^{-x}\right)+\frac{d}{d x}\left(x^{2}\right)\)
\(\Rightarrow \frac{d y}{d x}=a e^{x}+b e^{-x}+2 x\)
Now, Again differentiating both sides w.r.t. \( x \), we get,
\(\frac{d}{d x}\left(y^{\prime}\right)=\frac{d}{d x}\left(a e^{x}+b e^{-x}+2 x\right)\)
\(\Rightarrow \frac{d^{2} y}{d x^{2}}=a e^{x}+b e^{-x}+2\)
Now, Substituting the values of \( \frac{d y}{d x} \), and \( \frac{d^{2} y}{d x^{2}} \) in the given differential equations, we get,
\( \text {LHS }=x \frac{d^{2} y}{d x^{2}}+2 \frac{d y}{d x}-x y+x^{2}-2\)
\(={x}\left({ae}^{{x}}+{be}^{-{x}}+2\right)+2\left({ae}^{{x}}-{be}^{-{x}}+2\right)-{x}\left({ae}^{{x}}+{be}^{-{x}}+{x}^{2}\right)+{x}^{2}-2\)
\(=\left({axe}^{{x}}+{bxe^{- \textrm {x } } + 2 { x }}\right)+2\left({ae}^{{x}}-{be}^{-{x}}+2\right)-{x}\left({ae}^{{x}}+{be}^{-{x}}+{x}^{2}\right)+{x}^{2}-2\)
\(=2 {ae}^{{x}}-2 {be}^{-{x}}+{x}^{2}+6 {x}-2\)
\(\neq 0\)
\(\Rightarrow \text { LHS } \neq \text { RHS }\)
Therefore, the given function is not the solution of the corresponding differential equation.
2B. For each of the exercises given below, verify that the given function (implicit or explicit) is a solution of the corresponding differential equation.
\(y=e^{x}(a \cos x+b \sin x) ; \frac{d^{2} y}{d x^{2}}-2 \frac{d y}{d x}+2 y=0\)
\(y=e^{x}(a \cos x+b \sin x) ; \frac{d^{2} y}{d x^{2}}-2 \frac{d y}{d x}+2 y=0\)
Answer
It is given that \( =e^{x}(a \cos x+b \sin x)=a e^{x} \cos x+b e^{x} \sin x \)
Now, differentiating both sides w.r.t. \( x \), we get,
\(\frac{d y}{d x}=a \frac{d}{d x}\left(e^{x} \cos x\right)+b \frac{d}{d x}\left(e^{x} \sin x\right)\)
\(\Rightarrow \frac{d y}{d x}=a\left(e^{x} \cos x-e^{x} \sin x\right)+b\left(e^{x} \sin x-e^{x} \cos x\right)\)
\(\Rightarrow \frac{d y}{d x}=(a+b) e^{x} \cos x+(b-a) e^{x} \sin x\)
Now, again differentiating both sides w.r.t. \(x \), we get,
\( \frac{d^{2} y}{d x^{2}}=(a+b) \cdot \frac{d}{d x}\left(e^{x} \cos x\right)+(b-a) \frac{d}{d x}\left(e^{x} \sin x\right)\)
\(=(a+b) \cdot\left[e^{x} \cos x-e^{x} \sin x\right]+(b-a)\left[e^{x} \sin x-e^{x} \cos x\right]\)
\(=e^{x}[a \cos x-a \sin x+b \cos x-b \sin x+b \sin x+b \cos x-a \sin x-a \cos x] \)
\(=\left[2 e^{x}(b \cos x-a \sin x)\right] \)
Now, Substituting the values of \( \frac{d y}{d x} \), and \( \frac{d^{2} y}{d x^{2}} \) in the given differential equations, we get,
\(\text {LHS }=\frac{d^{2} y}{d x^{2}}+2 \frac{d y}{d x}+2 y\)
\(=2 {e}^{x}({b} \cos x-{a} \sin x)-2 {e}^{x}[({a}+{b}) \cos x+({b}-{a}) \sin x]\) \(+2 {e}^{x}({a} \cos x+{b} \sin x)\)
\(={e}^{x}[(2 {b} \cos x-2 {a} \sin x)-(2 {a} \cos x+2 {~b} \cos x)\) \(-(2 {b} \sin x-2 {a} \sin x)+(2 {a \cos} x+2 {b \sin} x)]\)
\(={e}^{x}[(2 {b}-2 {a}-2 {~b}+2 {a}) \cos x]+{e}^{x}[(-2 {a}-2 {b}+2 {a}+2 {~b} \sin x]\)
\(=0=\text { RHS }\)
Therefore, the given function is the solution of the corresponding differential equation.
2C. For each of the exercises given below, verify that the given function (implicit or explicit) is a solution of the corresponding differential equation.
\(y=x \sin 3 x ; \frac{d^{2} y}{d x^{2}}+9 y-6 \cos 3 x=0\)
\(y=x \sin 3 x ; \frac{d^{2} y}{d x^{2}}+9 y-6 \cos 3 x=0\)
Answer
It is given that \( =y=x \sin 3 x \)
Now, differentiating both sides w.r.t. \(x \), we get,
\(\frac{d y}{d x}=\frac{d}{d x}(x \sin 3 x)=\sin 3 x+x \cdot \cos 3 x \cdot 3\)
\(\Rightarrow \frac{d y}{d x}=\sin 3 x+3 x \cos 3 x\)
Now, again differentiating both sides w.r.t. \( x \), we get,
\(\frac{d^{2} y}{d x^{2}}=\frac{d}{d x}(x \sin 3 x)+3 \frac{d}{d x}(x \cos 3 x)\)
\(\Rightarrow \frac{d^{2} y}{d x^{2}}=3 x \cos 3 x+3[\cos 3 x+x(-\sin 3 x) .3]\)
\(\Rightarrow \frac{d^{2} y}{d x^{2}}=6 \cos 3 x-9 x \sin 3 x\)
Now, substituting the value of \( \frac{d^{2} y}{d x^{2}} \) in the LHS of the given differential equation, we get,
\(\frac{d^{2} y}{d x^{2}}+9 y-6 \cos 3 x\)
\(=(6 \cdot \cos 3 x-9 x \sin 3 x)+9 x \sin 3 x-6 \cos 3 x\)
\(=0=\text{RHS}\)
Therefore, the given function is the solution of the corresponding differential equation.
2D. For each of the exercises given below, verify that the given function (implicit or explicit) is a solution of the corresponding differential equation.
\(x^{2}=2 y^{2} \log y ;\left(x^{2}+y^{2}\right) \frac{d y}{d x}-x y=0\)
\(x^{2}=2 y^{2} \log y ;\left(x^{2}+y^{2}\right) \frac{d y}{d x}-x y=0\)
Answer
It is given that \( x^{2}=2 {y}^{2} \log {y} \)
Now, differentiating both sides w.r.t. \(x \), we get,
\(2 x=2 \cdot \frac{d}{d x}\left(y^{2} \log y\right)\)
\(\Rightarrow x=\left[2 y \cdot \log y \cdot \frac{d y}{d x}+y^{2} \cdot \frac{1}{y} \cdot \frac{d y}{d x}\right]\)
\(\Rightarrow x=\frac{d y}{d x}(2 y \log y+y)\)
\(\Rightarrow \frac{d y}{d x}=\frac{x}{y(1+2 \log y)}\)
Now, substituting the value of \( \frac{d y}{d x} \) in the LHS of the given differential equation, we get,
\(\left(x^{2}+y^{2}\right) \frac{d y}{d x}-x y=\left(2 y^{2} \log +y^{2}\right) \cdot \frac{x}{y(1+2 \log y)}-x y\)
\(=y^{2}(1+2 \log y) \cdot \frac{x}{y(1+2 \log y)}-x y\)
\(={xy}-{xy}\)
\(=0\)
Therefore, the given function is the solution of the corresponding differential equation.
3. Form the differential equation representing the family of curves given by \( (x-a)^{2}+2 y^{2}=a^{2} \), where \( a \) is an arbitrary constant.
Answer
It is given that \( (x-a)^{2}+2 y^{2}=a^{2} \)
\(\Rightarrow x^{2}+a^{2}-2 a x+2 y^{2}=a^{2}\)
\(\Rightarrow 2 y^{2}=2 a x-x^{2}\quad \ldots\ldots\text{(1)}\)
Now, differentiating both sides w.r.t. \( x \), we get,
\( 2 y \frac{d y}{d x}=\frac{2 a-2 x}{2} \)
\( \Rightarrow \frac{d y}{d x}=\frac{a-x}{2 y} \)
\( \Rightarrow \frac{d y}{d x}=\frac{2 a x-2 x^{2}}{4 x y} \quad \ldots\ldots\text{(2)}\)
So, equation (1), we get,
\(2 {ax}=2 {y}^{2}+x^{2}\)
On substituting this value in equation (3), we get,
\(\frac{d y}{d x}=\frac{2 y^{2}+x^{2}-2 x^{2}}{4 x y}\)
\(\Rightarrow \frac{d y}{d x}=\frac{2 y^{2}-x^{2}}{4 x y}\)
Therefore, the differential equation of the family of curves is given as \( \frac{d y}{d x}=\frac{2 y^{2}-x^{2}}{4 x y} \).
4. Prove that \( x^{2}-y^{2}=c\left(x^{2}+y^{2}\right)^{2} \) is the general solution of differential equation \( \left(x^{3}-3 x y^{2}\right) d x=\left(y^{3}-3 x^{2} y\right) d y \), where \( c \) is a parameter.
Answer
It is given that \( \left(x^{3}-3 x^{2}\right) d x=\left(y^{3}-3 x^{2} y\right) d y \)
\(\Rightarrow \frac{d y}{d x}=\frac{x^{3}-3 x y^{2}}{y^{3}-3 x^{2} y}\quad \ldots\ldots\text{(1)}\)
Now, let us take \( {y}={vx} \)
\(\Rightarrow \frac{d}{d x}(y)=\frac{d}{d x}(v x)\)
\(\Rightarrow \frac{{dy}}{{dx}}={v}+x \frac{{dv}}{{dx}}\)
Now, substituting the values of y and \( \frac{{dv}}{{dx}} \) in equation (1), we get,
\(v+x \frac{d v}{d x}=\frac{x^{3}-3 x(v x)^{2}}{(v x)^{3}-3 x^{2}(v x)}\)
\(\Rightarrow v+x \frac{d v}{d x}=\frac{1-3 v^{2}}{v^{3}-3 v}\)
\(\Rightarrow x \frac{d v}{d x}=\frac{1-3 v^{2}}{v^{3}-3 v}-v\)
\(\Rightarrow x \frac{d v}{d x}=\frac{1-3 v^{2}-v\left(v^{3}-3 v\right)}{v^{3}-3 v}\)
\(\Rightarrow \frac{v^{3}-3 v}{1-3 v^{4}} d v=\frac{d x}{x}\)
On integrating both sides we get,
\( \int \frac{v^{3}-3 v}{1-3 v^{4}} {~d} v=\log x+\log C^{\prime} \quad \ldots\ldots\text{(2)}\)
Now, \( \int \frac{v^{3}-3 v}{1-3 v^{4}} d v=\int \frac{v^{3}}{1-v^{4}} d v-3 \int \frac{v d v}{1-v^{4}} \)
\( \Rightarrow \int \frac{v^{3}-3 v}{1-3 {v}^{4}} {dv}={I}_{1}-3 {I}_{2} \) where \( {I}_{1} \int \frac{{v}^{3}}{1-{v}^{4}} {dv} \) and \( {I}_{2}=\int \frac{{vdv}}{1-{v}^{4}} \quad \ldots\ldots\text{(3)}\)
Let \( 1-{v}^{4}=t \)
\(\Rightarrow \frac{d}{d v}\left(1-v^{4}\right)=\frac{d t}{d v}\)
\(\Rightarrow-4 v^{3}=\frac{d t}{d v}\)
\(\Rightarrow v^{3} d v=-\frac{d t}{4}\)
Now, \( {I}_{1}=\int-\frac{{dt}}{4}=-\frac{1}{4} \log t=-\frac{1}{4} \log \left(1-{v}^{4}\right) \)
and \( {I}_{2}=\int \frac{{vdv}}{1-{v}^{4}}=\int \frac{{vdv}}{1-\left({v}^{2}\right)^{2}} \)
Let \( {v}^{2}={p} \)
\(\frac{{d}}{{dv}}\left({v}^{2}\right)=\frac{{dp}}{{dv}}\)
\(\Rightarrow 2 {v}=\frac{{dp}}{{dv}}\)
\(\Rightarrow {vdv}=\frac{d p}{2}\)
\(\therefore {I}_{2}=\frac{1}{2} \int \frac{{dt}}{1-{p}^{2}}=\frac{1}{2 \times 2} \log \left|\frac{1+p}{1-p}\right|=\frac{1}{4}\left|\frac{1+{v}^{2}}{1-{v}^{2}}\right|\)
Now, substituting the values of \( {I}_{1} \) and \( {I}_{2} \) in equation (3), we get,
\(\int\left(\frac{{v}^{3}-3 y}{1-{v}^{4}}\right) {dv}-\frac{3}{4} \log \left|\frac{1+{v}^{2}}{1-{v}^{2}}\right|\)
Thus, equation (2), becomes,
\(-\frac{1}{4} \log \left(1-{v}^{4}\right)-\frac{3}{4} \log \left|\frac{1+{v}^{2}}{1-{v}^{2}}\right|=\log x+\log C^{\prime}\)
\(\Rightarrow-\frac{1}{4} \log \left[\left(1-{v}^{4}\right)\left(\frac{1+{v}^{2}}{1-{v}^{2}}\right)^{3}\right]=\log C^{\prime} x\)
\(\Rightarrow \frac{\left(1+{v}^{2}\right)^{4}}{\left(1-{v}^{2}\right)^{2}}=\left(C^{\prime} x\right)^{-4}\)
\(\Rightarrow \frac{\left(1+\frac{y^{2}}{x^{2}}\right)^{4}}{\left(1-\frac{y^{2}}{x^{2}}\right)^{2}}=\frac{1}{C^{\prime 4} x^{4}}\)
\(\Rightarrow\left(x^{2}-y^{2}\right)^{2}=C^{\prime} 4\left(x^{2}+y^{2}\right)^{4}\)
\(\Rightarrow\left(x^{2}-y^{2}\right)=C^{\prime 2}\left(x^{2}+y^{2}\right)\)
\(\Rightarrow\left(x^{2}-y^{2}\right)=C\left(x^{2}+y^{2}\right), \text { where } {C}=C^{\prime 2}\)
Therefore, the result is proved.
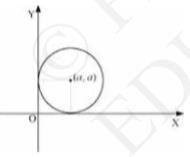
5. Form the differential equation of the family of circles in the first quadrant which touch the coordinate axes.
Answer
We know that the equation of a circle in the first quadrant with centre (a, a) and radius a which touches the coordinate axes is:
\((x-a)^{2}+(y-a)^{2}=a^{2}\quad \ldots\ldots\text{(1)}\)
Now differentiating above equation w.r.t. \(x \), we get,
\(2(x-{a})+2({y}-{a}) \frac{d y}{d x}=0\)
\(\Rightarrow(x-{a})+({y}-{a}) {y}^{\prime}=0\)
\(\Rightarrow x-{a}+{yy}^{\prime}-{ay}^{\prime}=0\)
\(\Rightarrow x+{yy}^{\prime}-{a}\left(1+{y}^{\prime}\right)=0\)
\(\Rightarrow {a}=\frac{x+y y^{\prime}}{1+y^{\prime}}\)
Now, substituting the value of a in equation (1), we get,
\({\left[x-\left(\frac{x+y y^{\prime}}{1+y^{\prime}}\right)\right]^{2}+\left[y-\left(\frac{x+y y^{\prime}}{1+y^{\prime}}\right)\right]^{2}=\left(\frac{x+y y^{\prime}}{1+y^{\prime}}\right)^{2}}\)
\(\Rightarrow\left[\frac{(x-y) y^{\prime}}{1+y^{\prime}}\right]^{2}+\left[\frac{y-x}{1+y^{\prime}}\right]^{2}=\left(\frac{x+y y^{\prime}}{1+y^{\prime}}\right)^{2}\)
\(\Rightarrow(x-{y})^{2} \cdot {y}^{\prime 2}+(x-{y})^{2}=\left(x+yy^{\prime}\right)^{2}\)
\(\Rightarrow(x-{y})^{2}\left[1+\left({y}^{\prime}\right)^{2}\right]=\left(x+y y^{\prime}\right)^{2}\)
Therefore, the required differential equation of the family of circles is
\((x-y)^{2}\left[1+\left(y^{\prime}\right)^{2}\right]=\left(x+y y^{\prime}\right)^{2}\)
miscellaneous exercise chapter 9 class 12 || differential equations class 12 ncert solutions || miscellaneous exercise class 12 chapter 9 || class 12 maths chapter 9 miscellaneous exercise solutions
6. Find the general solution of the differential equation
\(\frac{d y}{d x}+\sqrt{\frac{1-y^{2}}{1-x^{2}}}=0\)
\(\frac{d y}{d x}+\sqrt{\frac{1-y^{2}}{1-x^{2}}}=0\)
Answer
It is given that \( \frac{d y}{d x}+\sqrt{\frac{1-y^{2}}{1-x^{2}}}=0 \)
\(\Rightarrow \frac{d y}{d x}=-\sqrt{\frac{1-y^{2}}{1-x^{2}}}\)
\(\Rightarrow \frac{d y}{\sqrt{1-y^{2}}}=-\frac{d x}{\sqrt{1-x^{2}}}\)
On integrating, we get,
\(\sin ^{-1} y=\sin ^{-1} x+C\)
\(\Rightarrow \sin ^{-1} x=\sin ^{-1} y+C\)
7. Show that the general solution of the differential equation \( \frac{d y}{d x}+\frac{y^{2}+y+1}{x^{2}+x+1}=0 \) is given by \( (x+{y}+1)={A}(1-x-{y}-2 {xy}) ,\) where A is parameter.
Answer
It is given that \( \frac{d y}{d x}+\frac{y^{2}+y+1}{x^{2}+x+1}=0 \)
\(\Rightarrow \frac{d y}{d x}=-\left(\frac{y^{2}+y+1}{x^{2}+x+1}\right)\)
\(\Rightarrow \frac{d y}{y^{2}+y+1}=\frac{-d x}{x^{2}+x+1}\)
\(\Rightarrow \frac{d y}{y^{2}+y+1}+\frac{d x}{x^{2}+x+1}=0\)
On integrating both sides, we get,
\(\int \frac{d y}{y^{2}+y+1}+\int \frac{d x}{x^{2}+x+1}={C}\)
\(\Rightarrow \int \frac{d y}{\left(y+\frac{1}{2}\right)^{2}+\left(\frac{\sqrt{3}}{2}\right)^{2}}+\int \frac{d x}{\left(x+\frac{1}{2}\right)^{2}+\left(\frac{\sqrt{3}}{2}\right)^{2}}={C}\)
\(\Rightarrow \frac{2}{\sqrt{3}} \tan ^{-1}\left[\frac{y+\frac{1}{2}}{\frac{\sqrt{3}}{2}}\right]+\frac{2}{\sqrt{3}} \tan ^{-1}\left[\frac{x+\frac{1}{2}}{\frac{\sqrt{3}}{2}}\right]={C}\)
\(\Rightarrow \tan ^{-1}\left[\frac{2 y+1}{\sqrt{3}}\right]+\tan ^{-1}\left[\frac{2 x+1}{\sqrt{3}}\right]=\frac{\sqrt{3}}{2} {C}\)
\(\Rightarrow \tan ^{-1}\left[\frac{\frac{2 y+1}{\sqrt{3}}+\frac{2 x+1}{\sqrt{3}}}{1-\frac{2 y+1}{\sqrt{3}} \cdot \frac{12+1}{\sqrt{3}}}\right]=\frac{\sqrt{3}}{2} {C}\)
\(\Rightarrow \tan ^{-1}\left[\frac{2 \sqrt{3}(x+y+1)}{3-4 x y-2 x-2 y-1}\right]=\frac{\sqrt{3}}{2} {C}\)
\(\Rightarrow \tan ^{-1}\left[\frac{2 \sqrt{3}(x+y+1)}{2(1-x-y-2 x y)}\right]=\frac{\sqrt{3}}{2} {C}\)
\(\Rightarrow \frac{\sqrt{3}(x+y+1)}{(1-x-y-2 x y)}=\tan \left(\frac{\sqrt{3}}{2} {C}\right)\)
Let \( \tan \left(\frac{\sqrt{3}}{2} {C}\right)={B} \)
Then,
\(x+y+1=\frac{2 {B}}{\sqrt{3}}(1-x-y-2 x y)\)
Now, let \( A=\frac{2 B}{\sqrt{3}} \), then, we have,
\(x+y+1=A(1-x-y-2 x y)\)
8. Find the equation of the curve passing through the point \( \left(0, \frac{\pi}{4}\right) \) whose differential equation is \( \sin x \cos {y} d x+\cos x \sin {y} d y=0 \).
Answer
It is given that \( \sin x \cos {ydx}+\cos x \sin {ydy}=0 \)
\(\Rightarrow \frac{\sin x \cos y d x+\cos x \sin y d y}{\cos x \cos y}=0\)
\(\Rightarrow \tan x d x+\tan y d y=0\)
So, on integrating both sides, we get,
\(\log (\sec x)+\log (\sec {y})=\log {C}\)
\(\Rightarrow \log (\sec x \cdot \sec {y})=\log {C}\)
\(\Rightarrow \sec x \cdot \sec {y}=C\)
The curve passes through point \( \left(0, \frac{\pi}{4}\right) \)
Thus, \( 1 \times \sqrt{2}={C} \)
\(\Rightarrow {C}=\sqrt{2}\)
On substituting \( {C}=\sqrt{2} \) in equation (1), we get,
\(\sec x \cdot \sec {y}=\sqrt{2}\)
\(\Rightarrow \sec x \cdot \frac{1}{\cos y}=\sqrt{2}\)
\(\Rightarrow \cos y=\frac{\sec x}{\sqrt{2}}\)
Therefore, the required equation of the curve is \( \cos y=\frac{\sec x}{\sqrt{2}} \)
9. Find the particular solution of the differential equation \(( 1+ e^{2 x}) d y+(1+y^{2}) e^{x} d x=0 \), given that \( y=1 \) when \( x=0 \).
Answer
It is given that \( \left(1+e^{2 x}\right) d y+\left(1+y^{2}\right) e^{x} d x=0 \)
\(\Rightarrow \frac{d y}{1+y^{2}}+\frac{e^{x} d x}{1+e^{2 x}}=0\)
On integrating both sides, we get,
\(\tan ^{-1} y+\int \frac{e^{x} d x}{1+e^{2 x}}=C\quad \ldots\ldots\text{(1)}\)
Let \( {e}^{x}={t} \)
\(\Rightarrow {e}^{2 x}={t}^{2}\)
\(\Rightarrow \frac{d}{d x}\left(e^{x}\right)=\frac{d t}{d x}\)
\(\Rightarrow e^{x}=\frac{d t}{d x}\)
\(\Rightarrow {e}^{x} {dx}={dt}\)
Substituting the value in equation (1), we get,
\(\tan ^{-1} y+\int \frac{d t}{1+t^{2}}=C\)
\(\Rightarrow \tan ^{-1} {y}+\tan ^{-1} {t}={C}\)
\(\Rightarrow \tan ^{-1} {y}+\tan ^{-1}\left({e}^{x}\right)={C}\quad \ldots\ldots\text{(2)}\)
Now, \( {y}=1 \) at \( x=0 \)
Therefore, equation (2) becomes:
\(\tan ^{-1} 1+\tan ^{-1} 1={C}\)
\(\Rightarrow \frac{\pi}{4}+\frac{\pi}{4}={C}\)
\(\Rightarrow C=\frac{\pi}{4}\)
Substituting \( C=\frac{\pi}{4} \) in (2), we get,
\(\tan ^{-1} {y}+\tan ^{-1}\left({e}^{x}\right)=\frac{\pi}{4}\)
10. Solve the differential equation \( y e^{\frac{x}{y}}=\left(x e^{\frac{x}{y}}+y^{2}\right) d y(y \neq 0) \)
Answer
It is given that \( y e^{\frac{x}{y}}=\left(x e^{\frac{x}{y}}+y^{2}\right) d y \)
\(
\Rightarrow y e^{\frac{x}{y} }\frac{d x}{d y}=x e^{\frac{x}{y}}+y^{2}\)
\(
\Rightarrow e^{\frac{x}{y}}\left[y \cdot \frac{d x}{d y}-x\right]=y^{2}\)
\(
\Rightarrow e^{\frac{x}{y}} \frac{\left[y \cdot \frac{d x}{d y}-x\right]}{y^{2}}=1\quad \ldots\ldots\text{(1)}
\)
Let \( e^{\frac{x}{y}}=z \)
Differentiating it w.r.t. \(y\), we get,
\(\frac{d}{d y}\left(e^{\frac{x}{y}}\right)=\frac{d z}{d y}\)
\(\Rightarrow e^{\frac{x}{y}} \cdot \frac{d}{d y}\left(\frac{x}{y}\right)=\frac{d z}{d y}\)
\(\Rightarrow e^{\frac{x}{y}}\left[\frac{y \cdot \frac{d x}{d y}-x}{y^{2}}\right]=\frac{d z}{d y}\quad \ldots\ldots\text{(2)}\)
From equation (1) and equation (2), we get,
\(\frac{d z}{d y}=1\)
\(\Rightarrow {dz}={dy}\)
On integrating both sides, we get,
\({z}={y}+{C}\)
\(\Rightarrow e^{\frac{x}{y}}=y+C\)
11. Find a particular solution of the differential equation \(( x-y ) (d x+d y)=d x-d y \), given that \( y=-1 \), when \( x=0 \).
Answer
It is given that \( (x-y)(d x+d y)=d x-d y \)
\(\Rightarrow(x-{y}+1) {dy}=(1-x+{y}) {dx}\)
\(\Rightarrow \frac{d y}{d x}=\frac{1-x+y}{x-y+1}\)
\(\Rightarrow \frac{d y}{d x}=\frac{1-(x-y)}{x-y+1}\quad \ldots\ldots\text{(1)}\)
Let \( x-{y}={t} \)
\(\Rightarrow \frac{d(x-y)}{d x}=\frac{d t}{d x}\)
\(\Rightarrow 1-\frac{d y}{d x}=\frac{d t}{d x}\)
\(\Rightarrow 1-\frac{d t}{d x}=\frac{d y}{d x}\)
Now, let us substitute the value of \( x-y \) and \( \frac{d y}{d x} \) in equation (1), we get,
\(1-\frac{d t}{d x}=\frac{1-t}{1+t}\)
\(\Rightarrow \frac{d t}{d x}=1-\left(\frac{1-t}{1+t}\right)\)
\(\Rightarrow \frac{d t}{d x}=\frac{(1+t)-(1-t)}{1+t}\)
\(\Rightarrow \frac{d t}{d x}=\frac{2 t}{1+t}\)
\(\Rightarrow\left(\frac{1+t}{t}\right) d t=2 d x\)
\(\Rightarrow\left(1+\frac{1}{t}\right) d t=2 d x\quad \ldots\ldots\text{(2)}\)
On integrating both side, we get,
\({t}+\log |{t}|=2 x+{C}\)
\(\Rightarrow(x-{y})+\log |x-{y}|=2 x+{C}\)
\(\Rightarrow \log |x-{y}|=x+{y}+{C}\quad \ldots\ldots\text{(3)}\)
Now, \( {y}=-1 \) at \( x=0 \)
Then, equation (3), we get,
\(\log 1=0-1+C\)
\(\Rightarrow C=1\)
Substituting \( {C}=1 \) in equation (3), we get,
\(\log |x-y|=x+y+1\)
Therefore, a particular solution of the given differential equation is \( \log |x -{y} |=x+{y}+1 \).
miscellaneous exercise chapter 9 class 12 || differential equations class 12 ncert solutions || miscellaneous exercise class 12 chapter 9 || class 12 maths chapter 9 miscellaneous exercise solutions
12. Solve the differential equation \( \left[\frac{e^{-2 \sqrt{x}}}{\sqrt{x}}-\frac{y}{\sqrt{x}}\right] \frac{d x}{d y}=1(x \neq 0) \).
Answer
It is given that \( \left[\frac{e^{-2 \sqrt{x}}}{\sqrt{x}}-\frac{y}{\sqrt{x}}\right] \frac{d x}{d y}=1 \)
\(\Rightarrow \frac{d y}{d x}=\frac{e^{-2 \sqrt{x}}}{\sqrt{x}}-\frac{y}{\sqrt{x}}\)
\(\Rightarrow \frac{d y}{d x}+\frac{y}{\sqrt{x}}=\frac{e^{-2 \sqrt{x}}}{\sqrt{x}}\)
This is equation in the form of \( \frac{d y}{d x}+p y=Q \) (where, \( {p}=\frac{1}{\sqrt{x}} \) and \( {Q}=\frac{e^{-2 \sqrt{x}}}{\sqrt{x}} \))
Now, I.F. \( =e^{\int p d x}=e^{\int \frac{1}{\sqrt{x}} d x}=e^{2 \sqrt{x}} \)
Thus, the solution of the given differential equation is given by the relation:
\(\text { y(I.F.)}=\int(Q \times \text {I. F.}) d x+C\)
\(\Rightarrow y e^{2 \sqrt{x}}=\int\left(\frac{e^{-2 \sqrt{x}}}{\sqrt{x}} \times e^{2 \sqrt{x}}\right) d x+C\)
\(\Rightarrow y e^{2 \sqrt{x}}=\int \frac{1}{\sqrt{x}} d x+C\)
\(\Rightarrow y e^{2 \sqrt{x}}=2 \sqrt{x}+C\)
13. Find a particular solution of the differential equation \( \frac{d y}{d x}+y \cot x=4 x \operatorname{cosec} x(x \neq 0) \), given that \( {y}=0 \) when \( x=\frac{\pi}{2} \)
Answer
It is given that \( \frac{d y}{d x}+y \cot x=4 x \operatorname{cosec} x \)
This is equation in the form of \( \frac{d y}{d x}+p y=Q \) (where, \( {p}=\cot x \) and \( {Q}= \) \( 4 x \operatorname{cosec}x) \)
Now, I.F. \( =e^{\int p d x}=e^{\int \cot x d x}=e^{\log |\sin x|}=\sin x \)
Thus, the solution of the given differential equation is given by the relation:
\(\text {y(I.F.)}=\int(Q \times \text { I.F.}) d x+C\)
\(\Rightarrow y \sin x=\int 2 x \operatorname{cosec} x d x+C\)
\(=4 \int x d x+C\)
\(=4 . \frac{x^{2}}{2}+C\)
\(\Rightarrow y \sin x=2 x^{2}+C\quad \ldots\ldots\text{(1)}\)
Now \( {y}=0 \) at \( x=\frac{\pi}{2} \)
Therefore, equation (1), we get,
\( 0=2 \times \frac{\pi^{2}}{4}+C \)
\( \Rightarrow C=\frac{\pi^{2}}{4} \)
Now, substituting \( {C}=\frac{\pi^{2}}{4} \) in equation (1), we get,
\({y} \sin x=2 x^{2}-\frac{\pi^{2}}{4}\)
Therefore, the required particular solution of the given differential equation is
\({y} \sin x=2 x^{2}-\frac{\pi^{2}}{4}\)
14. Find a particular solution of the differential equation \( (x+1) \frac{d y}{d x}=2 e^{-y}-1 \), given that \( {y}=0 \) when \( x=0 \).
Answer
It is given that \( (x+1) \frac{d y}{d x}=2 e^{-y}-1 \)
\(\Rightarrow \frac{d y}{2 e^{-y}-1}=\frac{d x}{x+1}\)
\(\Rightarrow \frac{e^{y} d y}{2-e^{y}}=\frac{d x}{x+1}\)
On integrating both sides, we get,
\(\int \frac{{e}^{{y}} {dy}}{2-{e}^{{y}}}=\log |x+1|+\log {C}\quad \ldots\ldots\text{(1)}\)
Let \( 2-{e}^{{y}}=t \)
\(\therefore \frac{d}{d t}\left(2-{e}^{{y}}\right)=\frac{d t}{d y}\)
\(\Rightarrow-{e}^{{y}}=\frac{d t}{d y}\)
\(\Rightarrow {e}^{{y}} {dt}=-{dt}\)
Substituting value in equation (1), we get,
\(\int \frac{-{dt}}{{t}}=\log |x+1|+\log {C}\)
\(\Rightarrow-\log |{t}|=\log |{C}(x+1)|\)
\(\Rightarrow-\log \left|2-{e}^{{y}}\right|=\log |{C}(x+1)|\)
\(\Rightarrow \frac{1}{2-{e}^{{y}}}={C}(x+1)\)
\( \Rightarrow 2-{e}^{{y}}=\frac{1}{c(x+1)}\quad \ldots\ldots\text{(2)} \)
Now, at \( x=0 \) and \( y=0 \), equation (2) becomes,
\( \Rightarrow 2-1=\frac{1}{C} \)
\( \Rightarrow {C}=1 \)
Now, substituting the value of C I equation (2), we get,
\( \Rightarrow 2-{e}^{{y}}=\frac{1}{(x+1)} \)
\( \Rightarrow {e}^{{y}}=2-\frac{1}{(x+1)} \)
\( \Rightarrow {e}^{{y}}=\frac{2 x+2-1}{(x+1)} \)
\( \Rightarrow {e}^{{y}}=\frac{2 x+1}{(x+1)} \)
\( \Rightarrow y=\log \left|\frac{2 x+1}{x+1}\right| \cdot(x \neq-1) \)
Therefore, the required particular solution of the given differential equation is
\( y=\log \left|\frac{2 x+1}{x+1}\right| \cdot(x \neq-1) \)
15. The population of a village increases continuously at the rate proportional to the number of its inhabitants present at any time. If the population of the village was 20,000 in 1999 and 25000 in the year 2004, what will be the population of the village in 2009 ?
Answer
Let the population at any instant (t) be \( y \).
Now it is given that the rate of increase of population is proportional to the number of inhabitants at any instant.
\(\therefore \frac{d y}{d t} \alpha y\)
\(\Rightarrow \frac{d y}{d t}=k y(k \text { is a constant})\)
\(\Rightarrow \frac{d y}{y}=k d t\)
Now, integrating both sides, we get,
\(\log {y}={kt}+{C}\quad \ldots\ldots\text{(1)}\)
According to given conditions,
In the year \( 1999, {t}=0 \) and \( {y}=20000 \)
\(\Rightarrow \log 20000=C\quad \ldots\ldots\text{(2)}\)
Also, in the year \(2004, t=5 \) and \( {y}=25000 \)
\(\Rightarrow \log 25000={k} .5+{C}\)
\(\Rightarrow \log 25000=5 {k}+\log 20000\)
\(\Rightarrow 5 k=\log \left(\frac{25000}{20000}\right)=\log \left(\frac{5}{4}\right)\)
\(\Rightarrow k=\frac{1}{5} \log \left(\frac{5}{4}\right)\quad \ldots\ldots\text{(3)}\)
Also, in the year \(2009, t=10 \)
Now, substituting the values of \( {t}, {k} \) and c in equation (1), we get
\(\log y=10 \times \frac{1}{5} \log \left(\frac{5}{4}\right)+\log (20000)\)
\(\Rightarrow \log y=\log \left[20000 \times\left(\frac{5}{4}\right)^{2}\right]\)
\(\Rightarrow y=20000 \times \frac{5}{4} \times \frac{5}{4}\)
\(\Rightarrow y=31250\)
Therefore, the population of the village in 2009 will be 31250.
16. The general solution of the differential equation \( \frac{y d x-x d x}{y}= 0 \) is
A. \( x y=C \) B. \( x=C y^{2} \) C. \( y=C x \) D. \( {y}={Cx}^{2} \)
A. \( x y=C \) B. \( x=C y^{2} \) C. \( y=C x \) D. \( {y}={Cx}^{2} \)
Answer
It is given that \( \frac{y d x-x d x}{y}=0 \)
\(\Rightarrow \frac{y d x-x d x}{y}=0\)
\(\Rightarrow \frac{1}{x} d x-\frac{1}{y} d y=0\)
Integrating both sides, we get,
\(\log |x|-\log |{y}|=\log {k}\)
\(\Rightarrow \log \left|\frac{x}{y}\right|=\log k\)
\(\Rightarrow \frac{x}{y}=k\)
\(\Rightarrow y=\frac{1}{k} x\)
\( \Rightarrow {y}={Cx} \) where \( {C}=\frac{1}{k} \).
17. The general solution of a differential equation of the type \( \frac{d x}{d y}+{P}_{1} x={Q}_{1} \) is
A. \( x e^{\int {P}_{1} d y}=\int\left({Q}_{1} e^{\int {P}_{1} d y}\right) d x+C \)
B. \( y e^{\int {P}_{1} d y}=\int\left({Q}_{1} e^{\int {P}_{1} d y}\right) d x+C \)
C. \( x e^{\int {P}_{1} d y}=\int\left({Q}_{1} e^{\int {P}_{1} d y}\right) d y+C \)
D. \( x e^{\int {P}_{1} d y}=\int\left({Q}_{1} e^{\int {P}_{1} d y}\right) d x+C \)
A. \( x e^{\int {P}_{1} d y}=\int\left({Q}_{1} e^{\int {P}_{1} d y}\right) d x+C \)
B. \( y e^{\int {P}_{1} d y}=\int\left({Q}_{1} e^{\int {P}_{1} d y}\right) d x+C \)
C. \( x e^{\int {P}_{1} d y}=\int\left({Q}_{1} e^{\int {P}_{1} d y}\right) d y+C \)
D. \( x e^{\int {P}_{1} d y}=\int\left({Q}_{1} e^{\int {P}_{1} d y}\right) d x+C \)
Answer
The integrating factor of the given differential equation \( \frac{d x}{d y}+{P}_{1} x={Q}_{1} \) is \( e^{\int {P}_{1} d y} \).
Thus, the general solution of the differential equation is given by,
\(x({I} . {F} .)=\int({Q} \times {I} . {F} .) {dy}+{C}\)
\(\Rightarrow x . e^{\int {P}_{1} d y}=\int\left({Q}_{1} e^{\int {P}_{1} d y}\right) {dy}+{C}\)
18. The general solution of the differential equation \( e^{x} d y+(y e^{x}+2 x) d x=0 \) is
A. \( x ey +x^{2}=C \) B. \( x ey +y^{2}=C \) C. \( y ex +x^{2}=C \) D. \( y ey +x^{2}=C \)
A. \( x ey +x^{2}=C \) B. \( x ey +y^{2}=C \) C. \( y ex +x^{2}=C \) D. \( y ey +x^{2}=C \)
Answer
It is given that \( e^{x} d y+\left(y e^{x}+2 x\right) d x=0 \)
\(\Rightarrow e^{x} \frac{d y}{d x}+y e^{x}+2 x=0\)
\(\Rightarrow \frac{d y}{d x}+y=-2 x e^{-x}\)
This is equation in the form of \( \frac{d y}{d x}+p y=Q \) (where, \( {p}=1 \) and \( {Q}=-2 {xe}^{-x} \))
Now, I.F. \( =e^{\int p d x}=e^{\int d x}=e^{x} \)
Thus, the solution of the given differential equation is given by the relation:
\(\text {y(I.F.})=\int(Q \times \text {I. F.}) d x+C\)
\(\Rightarrow y e^{x}=\int\left(-2 x e^{-x} \times e^{x}\right) d x+C\)
\(\Rightarrow y e^{2 \sqrt{x}}=\int 2 x d x+C\)
\(\Rightarrow {ye}^{x}=-x^{2}+{C}\)
\(\Rightarrow {ye}^{x}+x^{2}={C}\)
