Ncert Solution Class 9 Maths Chapter 2 Exercise 2.3

Remainder Theorem: If \( f(x) \) is a polynomial and it is divided by another polynomial \( g(x) \), the remainder of this division equals to the value \( f(a) \), where \( a \) is the solution of polynomial \( g(x)=0 \)
for example: if \( x^{2}+2 \) is divided by \( x-1 \), then to find remainder.
Put \( x-1=0\ x=1 \) and now putting this value in \( x^{2}+1 \), we get \( 1+1=2 \) as the remainder.
\( f(x)=x^{3}+3 x^{2}+3 x+1 \)
Now let \( \mathrm{g}(\mathrm{x})=\mathrm{x}+1 \) So for finding remainder, put
\(g(x)=0 x+1=0 x=-1\)
So \( \mathrm{f}(-1) \) will be the remainder when \( \mathrm{f}(\mathrm{x}) \) is divided by \(\mathrm{g}(\mathrm{x}) \mathrm{f}(-1)=(-1)^{3}+3(-1)^{2}+3(-1)+1\)
\(\mathrm{f}(-1)=-1+3-3+1\)
\(\mathrm{f}(-1)=0\)
Hence, Remainder \(=0\)

Remainder Theorem: If \( f(x) \) is a polynomial and it is dividedby another polynomial \( g(x) \), the remainder of this division equals to the value \( f(a) \),where \( a \) is the solution of polynomial \( g(x)=0 \)
for example: if \( x^{2}+2 \) is divided by \( x-1 \), then to find remainder.
put \( x-1=0\ x=1 \) and now putting this value in \( x^{2}+1 \), we get \( 1+1=2 \) as the remainder.
\(f(x)=x^{3}+3 x^{2}+3 x+1\)
Now let \( g(x)=x-\frac{1}{2} \) So for finding remainder,
put \( g(x)=0 x-\frac{ 1 }{ 2 }=0 x\) \( =\frac{ 1 }{ 2 } \)
so, \( f(\frac{ 1 }{ 2 }) \) will be the remainder when \(\mathrm{f}(\mathrm{x}) \) is divided by \(\mathrm{g}(\mathrm{x})\mathrm{f}\left(\frac{1}{2}\right)=\left(\frac{1}{2}\right)^{3}+3\left(\frac{1}{2}\right)^{3}+\left(\frac{1}{2}\right)+1\)
\(=\frac{1}{8}+\frac{3}{4}+\frac{3}{2}+1\)
\(=\frac{1+6+12+8}{8}\)
\(=\frac{27}{8}\)
Hence, Remainder \( =\frac{27}{8} \)

Remainder Theorem: If \( f(x) \) is a polynomial and it is dividedby another polynomial \( g(x) \), the remainder of this division equals to the value \( f(a) \), where \( a \) is the solution of polynomial \( g(x)=0 \)
for example: if \( x^{2}+2 \) is divided by \( x-1 \), then to find remainder.
put \( x-1=0\ x=1 \) and now putting this value in \( x^{2}+1 \), we get \( 1+1=2 \) as the remainder.
\(f(x)=x^{3}+3 x^{2}+3 x+1\)
Now let \( \mathrm{g}(\mathrm{x})=\mathrm{x} \) So for finding remainder, put \(\mathrm{g}(\mathrm{x})=0 \mathrm{x}=0 \)
So, \( \mathrm{f}(0) \) will be the remainder when \(f(x) \) is divided by \(g(x) f(0)=(0)^{3}+3(0)^{2}+3(0)+1\)
\(f(0)=1\)
Hence, Remainder \( =1 \)

Remainder Theorem: If \( f(x) \) is a polynomial and it is dividedby another polynomial \( g(x) \), the remainder of this division equals to the value \( f(a) \),where \( a \) is the solution of polynomial \( g(x)=0 \)
for example: if \( x^{2}+2 \) is divided by \( x-1 \), then to find remainder.
put \( x-1=0\ x=1 \) and now putting this value in \( x^{2}+1 \), we get \( 1+1=2 \) as the remainder.
\(f(x)=x^{3}+3 x^{2}+3 x+1\)
Now let \( \mathrm{g}(\mathrm{x})=\mathrm{x}+\pi \)
So for finding remainder, put \( \mathrm{g}(\mathrm{x})=0 \mathrm{x}+\pi=0 \)
\(x=-\pi\)
So, \( f(-\pi) \) will be the remainder when \( f(x) \) is divided by
\(\mathrm{g}(\mathrm{x}) \mathrm{f}(-\pi)=(-\pi) 3+3(-\pi) 2+3(-\pi)+1\)
\(\mathrm{f}(-\pi)=-\pi 3+3 \pi 2-3 \pi+1\)
\(-\pi 3+3 \pi 2-3 \pi+1 \) will be the remainder

Remainder Theorem: If \( f(x) \) is a polynomial and it is dividedby another polynomial \( g(x) \), the remainder of this division equals to the value \( f(a) \),where \( a \) is the solution of polynomial \( g(x)=0 \)
for example: if \( x^{2}+2 \) is divided by \( x-1 \), then to find remainder.
put \( x-1=0\ x=1 \) and now putting this value in \( x^{2}+1 \), we get \( 1+1=2 \) as the remainder.
\( f(x)=x^{3}+3 x^{2}+3 x+1 \)
Now let \( g(x)=5+2 x \)
So for finding the remainder, \( g(x)=05+2 x=0 x=-\frac{5}{2} \)
So, \( f(-\frac{ 5 }{ 2 }) \) will be the remainder when \( f(x) \) is divided by \( g(x) \)
\(f\left(\frac{-5}{2}\right)=\left(\frac{-5}{2}\right)^{3}+3\left(\frac{-5}{2}\right)^{2}+3\left(\frac{-5}{2}\right)+1\)
\(=\frac{-125}{8}+\frac{75}{4}-\frac{15}{2}+1\)
\(=\frac{-27}{8}\)
\( f(-\frac{ 5 }{ 2 })=-\frac{ 27 }{ 8 } \) will be the remainder.

By long division method, we have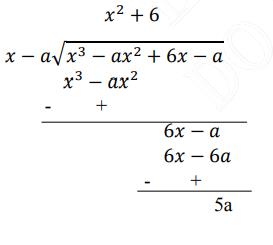

Therefore, the remainder obtained is \( 5 a \) when \( x^{3}-a x^{2}+6 x-a \) is divided by \(\mathrm{x}-\mathrm{a} \)
Remainder theorem:
Now to find the remainder when \( x^{3}-a x^{2}+6 x-a \) is divided by \( x-a \)
we have to put \( x-a=0 \), Thus \( x=a \)
Let \( f(x)=x^{3}-a x^{2}+6 x-a \) and \( f(a) \) will be the remainder \( f(a)=a^{3}-a \cdot a^{2}+6 a-a \)
\( f(a)=a^{3}-a^{3}+5 a \)
\( f(a)=5 a \)
Hence \(5 a\) is the remainder when \( x^{3}-a x^{2}+6 x-a \) is divided by \(\mathrm{x}-\mathrm{a} \).

To check for \( (3 x+7) \) be a factor of \( \left(3 x^{3}+7x\right) \)
We have to divide \( 3 x^{3}+7 x \) by \( 7+3 x \)
If remainder comes out be 0 then \( (7+3 x) \) will be a factor of \( \left(3 x^{3}+7 x\right)\).
By long division method,

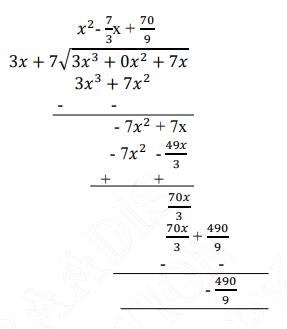
As remainder is not zero so \( (7+3 x) \) is not a factor of \( \left(3 x^{3}+7 x\right) \)
By Remainder theorem:
put \( 7+3 \mathrm{x}=0 \)
we get \( \mathrm{x}=\frac{ -7 }{ 3 } \) Now for checking out the remainder put x \( =\frac{ -7 }{ 3 } \) in \( \left(3 x^{3}+7 x\right) \)
we get, \( f\left(-\frac{7}{3}\right)=3\left(-\frac{7}{3}\right)^{3}+7\left(-\frac{7}{3}\right)\)
\(f\left(-\frac{7}{3}\right) =-\left(\frac{343}{9}\right)-\left(\frac{49}{3}\right)\)
\(=\frac{-343-147}{9}\)
\( f\left(-\frac{7}{3}\right)=-\frac{490}{9} \) which is not equal to zero and hence \( (7+3 x)\) is not a factor of \( \left(3 x^{3}+7 x\right) \)