Ncert exemplar class 9 maths solutions || class 9 maths ncert solution up board || cbse class 9 maths chapter 2 polynomials solutions || exercise 2.4 class 9 | class 9 maths ncert solutions chapter 2 exercise 2.4 class 9 | ncert solutions for class 9 maths chapter 2 exercise 2.4 class 9 | ncert solution class 9 maths chapter 2 exercise 2.4 class 9 | ncert solutions class 9 maths chapter 2 ex 2.4 || ncert solutions for class 9 maths || ncert class 9 maths chapter 2 polynomials solutions
Looking for Exercise 2.4 Class 9 Maths Solutions? Get step-by-step answers to Class 9 Chapter 2 Exercise 2.4 based on Polynomials. This exercise primarily deals with the factorisation of polynomials using algebraic identities and the factor theorem. Our comprehensive guide provides clear, easy-to-understand solutions for every question, helping students master the techniques required to break down complex polynomial expressions. These NCERT solutions are perfect for strengthening algebraic skills, preparing for exams and completing school assignments confidently. For further practice, students can also explore NCERT Exemplar Class 9 Maths problems to enhance their understanding.

ncert exemplar class 9 maths solutions || class 9 maths ncert solution up board || cbse class 9 maths chapter 2 polynomials solutions || exercise 2.4 class 9 | class 9 maths ncert solutions chapter 2 exercise 2.4 class 9 | ncert solutions for class 9 maths chapter 2 exercise 2.4 class 9 | ncert solution class 9 maths chapter 2 exercise 2.4 class 9 | ncert solutions class 9 maths chapter 2 ex 2.4 || ncert solutions for class 9 maths || ncert class 9 maths chapter 2 polynomials solutions
Exercise 2.4
1.
(i) Determine which of the following polynomials has \( (x+1) \)
a factor: \( x^{3}+x^{2}+x+1\)
Answer
To check for \( (\mathrm{x}+1) \) as a factor of given polynomials
by remainder theorem, we check for \( \mathrm{p}(-1)=0 \)If \( (\mathrm{x}+1) \) is a factor of \( \mathrm{p}(\mathrm{x})=x^{3}+x^{2}+x+1, p(-1) \) must be zero
Here, \( p(x)=x^{3}+x^{2}+x+1 \)
\(\mathrm{p}(-1)=(-1)^{3}+(-1)^{2}+(-1)+1\)
\(=-1+1-1+1=0\)
Therefore, \( \mathrm{x}+1 \) is a factor of this polynomial.
(ii) Determine which of the following polynomials has \( (x+1) \)
a factor: \(x^{4}+x^{3}+x^{2}+x+1 \)
Answer
To check for \( (\mathrm{x}+1) \) as a factor of given
polynomialsby remainder theorem, we check for \( \mathrm{p}(-1)=0
\)If \( (x+1) \) is a factor of \( p(x)=x^{4}+x^{3}+x^{2}+x+1, p(-1) \) must be zero
Here, \( p(x)=x^{4}+x^{3}+x^{2}+x+1 \)
\(\mathrm{p}(-1)=(-1)^{4}+(-1)^{3}+(-1)^{2}+(-1)+1\)
\(=1-1+1-1+1 \neq 0\)
Therefore, \( \mathrm{x}+1 \) is not a factor of this polynomial
(iii) Determine which of the following polynomials has \( (x+1)
\) a factor: \( x^{4}+3x^{3}+3 x^{2}+x+1 \)
Answer
To check for \( (\mathrm{x}+1) \) as a factor of given
polynomialsby remainder theorem, we check for \( \mathrm{p}(-1)=0
\)If \( (x+1) \) is a factor of \(p(x)=x^{4}+3 x^{3}+3 x^{2}+x+1, p(-1) \) must be zero
Here, \( p(x)=x^{4}+3 x^{3}+3 x^{2}+x+1 \)
\(\mathrm{p}(-1)=(-1)^{4}+3(-1)^{3}+3(-1)^{2}+(-1)+1\)
\(=1-3+3-1+1 \neq 0\)
Therefore, \( \mathrm{x}+1 \) is not a factor of this polynomial.
(iv) Determine which of the following polynomials has \( (x+1) \)
a factor: \(x^{3}-x^{2}-(2+\sqrt{2}) \mathrm{x}+\sqrt{2} \)
Answer
To check for \( (\mathrm{x}+1) \) as a factor of given
polynomialsby remainder theorem, we check for \( \mathrm{p}(-1)=0
\).If \( (x+1) \) is a factor of polynomial \( p(x)=x^{3}-x^{2}-(2+\sqrt{2}) x+\sqrt{2}, p(-1) \) must be zero
\( \mathrm{p}(-1)=(-1)^{3}-(-1)^{2}-(2+\sqrt{ 2} )(-1)+\sqrt{2 } \)
\( =-1-1+2+\sqrt{2 } +\sqrt{2 } \)
\(=2 \sqrt{2 } \)
As, \( p(-1) \neq 0 \)
Therefore, \( \mathrm{x}+1 \) is not a factor of this polynomial.
2.
(i) Use the Factor Theorem to determine whether \( g(x) \) is a
factor of \( \mathrm{p}(\mathrm{x}) \) in each of the following
cases:
\(\mathrm{p}(\mathrm{x})=2 x^{3}+x^{2}-2 x-1, g(x)=x+1 \)
\(\mathrm{p}(\mathrm{x})=2 x^{3}+x^{2}-2 x-1, g(x)=x+1 \)
Answer
If \( g(x)=x+1 \) is a factor of given polynomial \( p(x), p(-1)
\)must be zero\(\mathrm{p}(\mathrm{x})=2 \mathrm{x}^{3}+\mathrm{x}^{2}-2 \mathrm{x}-1\)
\(\mathrm{p}(-1)=2(-1)^{3}+(-1)^{2}-2(-1)-1\)
\(=2(-1)+1+2-1=0\)
Hence, \( \mathrm{g}(\mathrm{x})=\mathrm{x}+1 \) is a factor of given polynomial
(ii) Use the Factor Theorem to determine whether \( g(x) \) is a
factor of \( \mathrm{p}(\mathrm{x}) \) in each of the following
cases:
\(\mathrm{p}(\mathrm{x})=x^{3}+3 x^{2}+3 x+1, g(x)=x+2 \)
\(\mathrm{p}(\mathrm{x})=x^{3}+3 x^{2}+3 x+1, g(x)=x+2 \)
Answer
If \( g(x)=x+2 \) is a factor of given polynomial \( p(x), p(-2)
\)must be zero\(p(x)=x^{3}+3 x^{2}+3 x+1\)
\(p(-2)=(-2)^{3}+3(-2)^{2}+3(-2)+1\)
\(=-8+12-6+1=-1\)
As, \( \mathrm{p}(-2) \neq 0 \)
Hence, \( \mathrm{g}(\mathrm{x})=\mathrm{x}+2 \) is not a factor of given polynomial.
(iii) Use the Factor Theorem to determine whether \( g(x) \) is a
factor of \( \mathrm{p}(\mathrm{x}) \) in each of the following
cases:
\(\mathrm{p}(\mathrm{x})=x^{3}-4 x^{2}+\mathrm{x}+6, g(x)=x-3 \)
\(\mathrm{p}(\mathrm{x})=x^{3}-4 x^{2}+\mathrm{x}+6, g(x)=x-3 \)
Answer
If \( g(x)=x-3 \) is a factor of given polynomial \( p(x), p(3)
\)must be zero\(p(x)=x^{3}-4 x^{2}+x+6\)
\(p(3)=(3)^{3}-4(3)^{2}+3+6\)
\(=27-36+9=0\)
Therefore, \( \mathrm{g}(\mathrm{x})=\mathrm{x}-3 \) is a factor of the given polynomial.
ncert exemplar class 9 maths solutions || class 9 maths ncert solution up board || cbse class 9 maths chapter 2 polynomials solutions || exercise 2.4 class 9 | class 9 maths ncert solutions chapter 2 exercise 2.4 class 9 | ncert solutions for class 9 maths chapter 2 exercise 2.4 class 9 | ncert solution class 9 maths chapter 2 exercise 2.4 class 9 | ncert solutions class 9 maths chapter 2 ex 2.4 || ncert solutions for class 9 maths || ncert class 9 maths chapter 2 polynomials solutions
3.
(i) Find the value of \( k \), if is a factor of \( p(x) \) in
each ofthe following cases:
\(\mathrm{p}(\mathrm{x})=x^{2}+\mathrm{x}+\mathrm{k} \)
\(\mathrm{p}(\mathrm{x})=x^{2}+\mathrm{x}+\mathrm{k} \)
Answer
If \( g(x) \) is a factor of another polynomial \( p(x) \)
then,the points at which \( \mathrm{g}(\mathrm{x})=0,\
\mathrm{p}(\mathrm{x}) \) will also be equal to 0for example: Let \( p(x)=x^{2}-1 \) and \( g(x)=x+1 \)
By remainder theorem Now if \( x+1 \) is a factor of \( p(x) \), then \( x+1=0 \)
\( x \)\( =-1 \) at this value \( p(x)=0 \) Thus, \( p(-1)=0\)
If \( x-1 \) is a factor of polynomial \( p(x)=x^{2}+x+k \), then
\( \mathrm{x}-1=0 \mathrm{x}=1 \)
Therefore, \( \mathrm{p}(1)=0 \)
\((1)^{2}+1+k=0\)
\(2+k=0\)
\(k=-2\)
Therefore, value of \( k \) is \(-2\)
(ii) Find the value of \( k \), if is a factor of \( p(x) \) in
each ofthe following cases:
\(\mathrm{p}(\mathrm{x})=2 x^{2}+\mathrm{kx}+\sqrt{2} \)
\(\mathrm{p}(\mathrm{x})=2 x^{2}+\mathrm{kx}+\sqrt{2} \)
Answer
If \( g(x) \) is a factor of another polynomial \( p(x) \) then,
the points at which \( \mathrm{g}(\mathrm{x})=0,\
\mathrm{p}(\mathrm{x}) \) will also be equal to 0for example: Let \( p(x)=x^{2}-1 \) and \( g(x)=x+1 \)
By remainder theorem Now if \( x+1 \) is a factor of \( p(x) \), then \( x+1=0 \)
\( x \)\( =-1 \) at this value \( p(x)=0 \) Thus, \( p(-1)=0\)
If \( \mathrm{x}-1 \) is a factor ofpolynomial \( \mathrm{p}(\mathrm{x})=2 \mathrm{x}^{2}+\mathrm{kx}+\sqrt{2} \), then
\(\mathrm{p}(1)=0\)
\(2(1)^{2}+\mathrm{k}(1)+\sqrt{2}=0\)
\(2+\mathrm{k}+\sqrt{2}=0\)
\(\mathrm{k}=-2-\sqrt{2}\)
\(=-(2+\sqrt{2})\)
Therefore, value of \( k \) is \( -(2+\sqrt{2}) \)
(iii) Find the value of \( k \), if is a factor of \( p(x) \) in
each ofthe following cases:
\(\mathrm{p}(\mathrm{x})=k x^{2}-\sqrt{2} x+1 \)
\(\mathrm{p}(\mathrm{x})=k x^{2}-\sqrt{2} x+1 \)
Answer
If \( g(x) \) is a factor of another polynomial \( p(x) \)
then,the points at which \( \mathrm{g}(\mathrm{x})=0,\
\mathrm{p}(\mathrm{x}) \) will also be equal to 0for example: Let \( p(x)=x^{2}-1 \) and \( g(x)=x+1 \)
By remainder theorem Now if \( x+1 \) is a factor of \( p(x) \), then \( x+1=0 \)
\( x \)\( =-1 \) at this value \( p(x)=0 \) Thus, \( p(-1)=0\)
If \( x-1 \) is a factor of given polynomial \( p(x)=k x^{2}-x+1 \), then
\(\mathrm{p}(1)=0\)
\(\mathrm{k}(1)^{2}-(1)+1=0\)
\(\mathrm{k}-\sqrt{2}+1=0\)
\(\mathrm{k}=-1\)
Therefore, value of \( k \) is \( \sqrt{ 2} -1 \)
(iv) Find the value of \( k \), if is a factor of \( p(x) \) in
each ofthe following cases:
\(\mathrm{p}(\mathrm{x})=k x^{2}-3 x+k \)
\(\mathrm{p}(\mathrm{x})=k x^{2}-3 x+k \)
Answer
If \( g(x) \) is a factor of another polynomial \( p(x) \)
then,the points at which \( \mathrm{g}(\mathrm{x})=0,\
\mathrm{p}(\mathrm{x}) \) will also be equal to 0for example: Let \( p(x)=x^{2}-1 \) and \( g(x)=x+1 \)
By remainder theorem Now if \( x+1 \) is a factor of \( p(x) \), then \( x+1=0 \)
\( x \)\( =-1 \) at this value \( p(x)=0 \) Thus, \( p(-1)=0\)
If \( x-1 \) is a factor of the given polynomial \( p(x)=k x^{2}-3 x+k \), then \( \mathrm{p}(1)=0 \)
\(k(1)^{2}+3(1)+k=0\)
\(k-3+k=0\)
\(2 k-3=0\)
\(k=\frac{3}{2}\)
Therefore, value of \( k \) is \( \frac{3}{2} \)
4.
ncert exemplar class 9 maths solutions || class 9 maths ncert solution up board || cbse class 9 maths chapter 2 polynomials solutions || exercise 2.4 class 9 | class 9 maths ncert solutions chapter 2 exercise 2.4 class 9 | ncert solutions for class 9 maths chapter 2 exercise 2.4 class 9 | ncert solution class 9 maths chapter 2 exercise 2.4 class 9 | ncert solutions class 9 maths chapter 2 ex 2.4 || ncert solutions for class 9 maths || ncert class 9 maths chapter 2 polynomials solutions
(i) Factorize: \( 12x^{2}-7 x+1 \)
Answer
For quadratic polynomial. We factorize the middle term such
thatthe product of the terms is equal to the product of the last
term and coefficient of \( x^{2} \)and sum or difference is equal
to the middle term.\( 12 \mathrm{x}^{2}-7 \mathrm{x}+1 \)
For the equation given above: 7 is to be factorized such that, the product of two terms is \( 12\times 1=12 \) and the sum is equal to 7
This can be done by 3 and 4 as \( 3 \times 4=12 \) and \( 3+4=7 \)
Therefore, \(12 x^{2}-7 x+1\)
\(= 12 x^{2}-4 x-3 x+1\)
\(= 4 x(3 x-1)-1(3 x-1)\)
\(= (3 x-1)(4 x-1)\)
(ii) Factorize: \( 2x^{2}+7 x+3 \)
Answer
For quadratic polynomial. We factorize the middle term such that
the product of the terms is equal to the product of the last term
and coefficient of \( x^{2} \) and sum or difference is equal to
the middle term.\( 2 x^{2}+7 x+3 \)
For the equation given above: 7 is to be factorized such that, the product of two terms is \( 3\times 2=6 \) and the sum is equal to 7
This can be done by 6 and 1 as \( 6 \times 1=6 \) and \(6+1=7 \)
Therefore, \( 2 x^{2}+7 x+3=2 x^{2}+6 x+x+3 \)
\(=2 x(x+3)+1(x+3)\)
\(=(x+3)(2 x+1)\)
(iii) Factorize: \( 6x^{2}+5 x-6 \)
Answer
For quadratic polynomial. We factorize the middle term such that
the product of the terms is equal to the product of the last term
and coefficient of \( x^{2} \) and sum or difference is equal to
the middle term.\( 6 x^{2}+5 x-6 \)
For the equation given above: 7 is to be factorized such that, the product of two terms is \( 6 \times 6=36 \) and the difference is equal to 5
This can be done by 9 and 4 as \( 9 \times 4=36 \) and \( 9-4=5 \)Therefore, \(6 x^{2}+5 x-6=6 x^{2}+9 x-4 x-6\)
\(=3 x(2 x+3)-2(2 x+3)\)
\(=(2 x+3)(3 x-2)\)
ncert exemplar class 9 maths solutions || class 9 maths ncert solution up board || cbse class 9 maths chapter 2 polynomials solutions || exercise 2.4 class 9 | class 9 maths ncert solutions chapter 2 exercise 2.4 class 9 | ncert solutions for class 9 maths chapter 2 exercise 2.4 class 9 | ncert solution class 9 maths chapter 2 exercise 2.4 class 9 | ncert solutions class 9 maths chapter 2 ex 2.4 || ncert solutions for class 9 maths || ncert class 9 maths chapter 2 polynomials solutions
(iv) Factorize: \( 3x^{2}-x-4 \)
Answer
For quadratic polynomial. We factorize the middle term such that
the product of the terms is equal to the product of the last term
and coefficient of \( x^{2} \) and sum or difference is equal to
the middle term.\( 3 x^{2}-x-4 \)
For the equation given above: 7 is to be factorized such that, the product of two terms is \( 4\times 3=12 \) and the difference \( =1 \)
This can be done by 4 and 3 as \( 4 \times 3=12 \) and \( 4-3=1 \) Therefore, \(3 x^{2}-x-4=3 x^{2}-4 x+3 x-4\)
\(=(3 x-4)(x+1)\)
\(=x(3 x-4)+1(3 x-4)\)
\(=(3 x-4)(x+1)\)
5.
(i) Factorize: \( x^{3}-2 x^{2}-x+2 \)
Answer
Let \( \mathrm{p}(\mathrm{x})=\mathrm{x}^{3}-2
\mathrm{x}^{2}-\mathrm{x}+2 \)By trial method, we find that
\( \mathrm{p}(-1)=(-1)^{3}-2(-1)^{2}-(-1)+2\)
\(=-1-2+1+2=0 \)
Therefore, \( x=-1 \) satisfies the equation and \( (x+1) \) is the factor of \( p(x) \)
Now, we divide \( \mathrm{p}(\mathrm{x})=\mathrm{x}^{3}-2 \mathrm{x}-\mathrm{x}+2 \) by \( (\mathrm{x}+1) \)
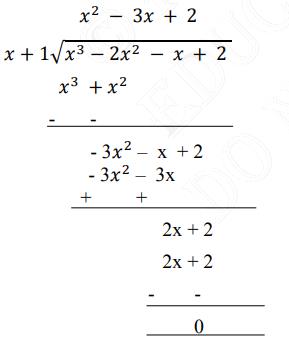
Now, Dividend \( =( \) Divisor \( \times \) Quotient \( )+ \) Remainder
\(\mathrm{p}(\mathrm{x})=(\mathrm{x}+1)\left(\mathrm{x}^{2}-3 \mathrm{x}+2\right)\)
\(=(\mathrm{x}+1)\left(\mathrm{x}^{2}-\mathrm{x}-2 \mathrm{x}+2\right)\)
\(=(\mathrm{x}+1)\{\mathrm{x}(\mathrm{x}-1)-2(\mathrm{x}-1)\}\)
\(=(\mathrm{x}+1)(\mathrm{x}-1)(\mathrm{x}-2)\)
(ii) Factorize: \(\mathrm{x}^{3}-3 \mathrm{x}^{2}-9 x-5 \)
Answer
Let \( \mathrm{p(x)}=x^{3}-3 x^{2}-9 x-5 \)By trial method,
\(\mathrm{p}(5)=(5)^{3}-3(5)^{2}-9(5)-5\)
\(=125-75-45-5=0\)
Therefore, \( (x-5) \) is the factor of \( p(x) \)
Now, we divide \( \mathrm{p}(\mathrm{x})=\mathrm{x}^{3}-3 \mathrm{x}^{2}-9 \mathrm{x}-5 \) by \((\mathrm{x}-5) \)
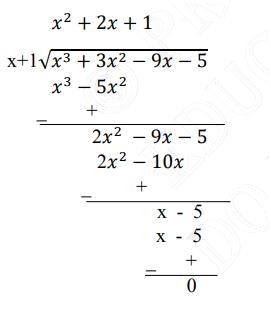
(iii) Factorize: \(\mathrm{x}^{3}+13 \mathrm{x}^{2}+32
\mathrm{x}+20 \)
Answer
Let \( \mathrm{p}(\mathrm{x})=\mathrm{x}^{3}+13
\mathrm{x}^{2}+32\mathrm{x}+20 \)By trial method,
\(\mathrm{p}(-1)=(-1)^{3}+13(-1)^{2}+32(-1)+20\)
\(=-1+13-32+20=0\)
Therefore, \( x=-1 \) satisfies the equation \( p(x)=0 \) so, \( (x+1) \) is the factor of \(\mathrm{p}(\mathrm{x}) \)
Now we divide \( \mathrm{p}(\mathrm{x})=\mathrm{x}^{3}+13 \mathrm{x}^{2}+32 \mathrm{x}+20 \) by\( (\mathrm{x}+1) \)
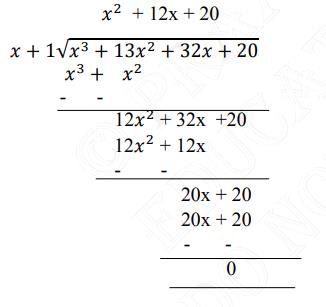
Now, Dividend \( =( \) Divisor \( \times \) Quotient \( )+ \) Remainder
\(\mathrm{p}(\mathrm{x})=(\mathrm{x}+1)\left(\mathrm{x}^{2}+12 \mathrm{x}+20\right)\)
\(=(\mathrm{x}+1)\left(\mathrm{x}^{2}+2 \mathrm{x}+10 \mathrm{x}+20\right)\)
\(=(\mathrm{x}+1)\{\mathrm{x}(\mathrm{x}+2)+10(\mathrm{x}+2)\}\)
\(=(\mathrm{x}+1)(\mathrm{x}+2)(\mathrm{x}+10)\)
(iv) Factorize: \( 2y^{3}+y^{2}-2 y-1 \)
Answer
Let, \( \mathrm{p}(\mathrm{y})=2
\mathrm{y}^{3}+\mathrm{y}^{2}-2\mathrm{y}-1 \) By trial method,
\(\mathrm{p}(1)=2(1)^{3}+(1)^{2}-2(1)-1\)
\(=2+1-1-1=0\)
Therefore, \( y=1 \) satisfies the equation \( p(y)=0 \) so, \( (y-1) \) is a factor of \(\mathrm{p}(\mathrm{y}) \)
Now, we divide \( \mathrm{p}(\mathrm{y})=2 \mathrm{y}^{3}+\mathrm{y}^{2}-2 \mathrm{y}-1 \) by \((\mathrm{y}-1) \)
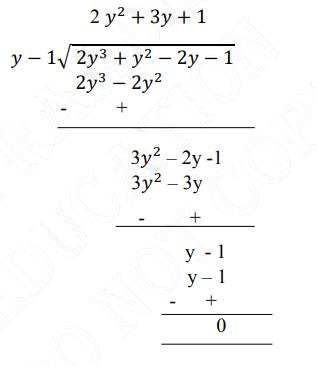
Now, Dividend \( =( \) Divisor \( \times \) Quotient \( )+ \) Remainder
\(p(y)=(y-1)\left(2 y^{2}-3 y+1\right)\)
\(=(y-1)\left(2 y^{2}-2 y-y+1\right)\)
\(=(y-1)\{2 y(y-1)-1(y-1)\}\)
\(=(y-1)(2 y-1)(y-1)\)

