Chapter 4 maths class 9 exercise 4.2 question 4 || ncert maths class 9 chapter 4 exercise 4.2 question 4 || linear equations in two variables class 9 extra questions || maths chapter 4 exercise 4.2 class 9 || ncert solutions for class 9 maths ch 4 ex 4.2 || maths class 9 exercise 4.2 || class 9 chapter 4 exercise 4.2 maths || exercise 4.2 class 9 maths || math chapter 4 class 9 exercise 4.2 || class 9 maths chapter 4 exercise 4.2 solutions
Discover clear, step-by-step solutions for Class 9 Maths Chapter 4, Exercise 4.2, centred on Linear Equations in Two Variables. This exercise deepens students’ grasp of how such equations inherently possess infinitely many solutions and how we can generate and verify specific ordered pairs. By engaging with these problems, learners refine their algebraic reasoning and prepare for more advanced topics. Exercise 4.2 highlights the infinite-solution feature of linear equations in two variables—explaining why, for any value of x, there exists a corresponding y that satisfies the equation.
chapter 4 maths class 9 exercise 4.2 question 4 || ncert maths class 9 chapter 4 exercise 4.2 question 4 || linear equations in two variables class 9 extra questions || maths chapter 4 exercise 4.2 class 9 || ncert solutions for class 9 maths ch 4 ex 4.2 || maths class 9 exercise 4.2 || class 9 chapter 4 exercise 4.2 maths || exercise 4.2 class 9 maths || math chapter 4 class 9 exercise 4.2 || class 9 maths chapter 4 exercise 4.2 solutions
Exercise 4.2
1. Which one of the following options is true, and why? \( {y}=3 {x}+5 \) has
(i) A unique solution,
(ii) Only two solutions,
(iii) Infinitely many solutions
(i) A unique solution,
(ii) Only two solutions,
(iii) Infinitely many solutions
Answer
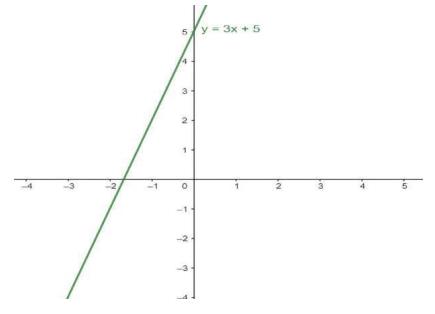
Equation \( {y}=3 {x}+5 \) is a linear equation in two variables.This means that we can put any value of \( x \) and in return, we will get some other value of \( y \).
For example, at \( x=0, y=3 x 0+5, y=5 \) at \( x=1000 \), \( y \) \( =3 \times 1000+5, y=3005\)
we can put infinitely many values of \(x\) and we will get infinitely many solutions for \( y \).
Thus there are infinite solutions for the equation.
Graphically: When plotted graphically, it will give a straight line extending to infinity and thus will give infinite solutions.
2. Write four solutions for each of the following equations:
(i) \( 2 x+y=7 \)
Answer
For finding out solutions for any linear equation in 2 variables, just put one value in any of the variable in the equation and obtain the other value.For example: For equation \(x + y = 5\) Let \(x = 1\), then \(1 + y = 5, y = 5 - 1, y = 4\) Thus \(x =1\) and \(y = 4\) will be a solution for the equation \(x + y = 5.\)
\( 2 x+y=7 \)
Given Equation: \( 2 {x}+{y}=7 \)
rearranging the equation, we get,
\(y=7-2 x\)
\(\text {Put } x=0\)
\(y=7-2 \times 0\)
\(y=7\)
\( (0,7) \) is the solution of the equation
Now,
Put \( x=1 \)
\(y=7-2 \times 1\)
\(y=5\)
\( (1,5) \) is the solution of the equation
Now,
Put \( {x}=2 \)
\(y=7-2 \times 2\)
\(y=3\)
\( (2,3) \) is the solution of the equation
Now,
Put \( x=-1 \)
\(y=7-2 x-1\)
\(y=9\)
\( (-1,9) \) is the solution of the equation
The four solutions of the equation \( 2 x+y=7 \) are:
\( (0,7) \),
\( (1,5) \),
\( (2,3) \)
and \( (-1,9) \)
(ii) \( \pi x+y=9 \)
Answer
For finding out solutions for any linear equation in 2 variables, just put one value in any of the variable in the equation and obtain the other value.For example: For equation \(x + y = 5\) Let \(x = 1\), then \(1 + y = 5, y = 5 - 1, y = 4\) Thus \(x =1\) and \(y = 4\) will be a solution for the equation \(x + y = 5.\)
\( \pi x+y=9 \)
\( \pi x+y=9 \)
\( y=9-\pi x \)
Now,
Put \( x=0 \)
\( y=9-\pi \times 0 \)
\( y=9 \)
\( (0,9) \) is the solution of the equation
Now,
Put \( {x}=1 \)
\(y=9-\pi \times 1\)
\(y=9-\pi\)
\( (1,9-\pi) \) is the solution of the equation
Now
Put \( {x}=2 \)
\(y=9-\pi \times 2\)
\(y=9-2 \pi\)
\( (2,9-2 \pi) \) is the solution of the equation
Now,
Put \( x=-1 \)
\(y=9-\pi \times(-1)\)
\(y=9+\pi\)
\( (-1,9+\pi) \) is the solution of the equation
The four solutions of the equation \( \pi x+y=9 \) are:
\((0,9),\)
\((1,9-\pi),\)
\( (2,9-2 \pi) \)
and \( (-1,9+\pi) \)
(iii) \( x=4 y \)
Answer
For finding out solutions for any linear equation in 2 variables, just put one value in any of the variable in the equation and obtain the other value.For example: For equation \(x + y = 5\) Let \(x = 1\), then \(1 + y = 5, y = 5 - 1, y = 4\) Thus \(x =1\) and \(y = 4\) will be a solution for the equation \(x + y = 5.\)
\( x=4 y \)
Now,
Put \( {x}=0 \)
\( 0=4 y \)
\( y=0 \)
\( (0,0) \) is the solution of the equation
Now,
put \( {x}=1 \)
\( 1=4 y \)
\( y=\frac{1}{4} \)
\( ( 1, \frac{1}{4} )\) is the solution of the equation
Now,
Put \( {x}=4 \)
\( 4=4 y \)
\( y=1 \)
\( (4,1) \) is the solution of the equation
Now, Put \( {x}=8 \)
\( 8=4 y \)
\( y=2 \)
\( (8,2) \) is the solution of the equation
The four solutions of the equation \( \pi x+y=9 \) are:
\( (0,0) \),
\( \left(1, \frac{1}{4}\right) \),
\( (4,1) \),
and \( (8,2) \)
3. Check which of the following are solutions of the equation \( x -2 {y}=4 \) and which are not:
chapter 4 maths class 9 exercise 4.2 question 4 || ncert maths class 9 chapter 4 exercise 4.2 question 4 || linear equations in two variables class 9 extra questions || maths chapter 4 exercise 4.2 class 9 || ncert solutions for class 9 maths ch 4 ex 4.2 || maths class 9 exercise 4.2 || class 9 chapter 4 exercise 4.2 maths || exercise 4.2 class 9 maths || math chapter 4 class 9 exercise 4.2 || class 9 maths chapter 4 exercise 4.2 solutions
(i) \( (0,2) \)
Answer
For a linear equation a point will be its solution, if it satisfies the equation.So put the points directly in the equation given, if the equation is satisfied, it is a solution or else it is not. Given Equation: \( x-2 y=4\)
Put \( x=0 \)
And
\( y=2 \)
In the equation \( x-2 y=4 \)
\( 0-2 \times 2=4 \)
\( -4 \neq 4 \)
Therefore,
\( (0,2) \) isn't a solution of the given equation
chapter 4 maths class 9 exercise 4.2 question 4 || ncert maths class 9 chapter 4 exercise 4.2 question 4 || linear equations in two variables class 9 extra questions || maths chapter 4 exercise 4.2 class 9 || ncert solutions for class 9 maths ch 4 ex 4.2 || maths class 9 exercise 4.2 || class 9 chapter 4 exercise 4.2 maths || exercise 4.2 class 9 maths || math chapter 4 class 9 exercise 4.2 || class 9 maths chapter 4 exercise 4.2 solutions
chapter 4 maths class 9 exercise 4.2 question 4 || ncert maths class 9 chapter 4 exercise 4.2 question 4 || linear equations in two variables class 9 extra questions || maths chapter 4 exercise 4.2 class 9 || ncert solutions for class 9 maths ch 4 ex 4.2 || maths class 9 exercise 4.2 || class 9 chapter 4 exercise 4.2 maths || exercise 4.2 class 9 maths || math chapter 4 class 9 exercise 4.2 || class 9 maths chapter 4 exercise 4.2 solutions
(ii) \( (2,0) \)
Answer
For a linear equation a point will be its solution, if it satisfies the equation.So put the points directly in the equation given, if the equation is satisfied, it is a solution or else it is not. Given Equation: \( x-2 y=4\)
Put \( {x}=2 \)
And
\( y=0 \)
In the equation \( x-2 y=4 \)
\( 2-2 \times 0=4 \)
\( 2 \neq 4 \)
Therefore,
\( (2,0) \) isn't a solution of the given equation
(iii) \( (4,0) \)
Answer
For a linear equation a point will be its solution, if it satisfies the equation.So put the points directly in the equation given, if the equation is satisfied, it is a solution or else it is not. Given Equation: \( x-2 y=4\)
Put \( {x}=4 \)
And
\( y=0 \)
In the equation \( x-2 y=4 \)
\(4-2 * 0=4\)
\(4=4\)
Therefore,
\( (4,0) \) is a solution of the equation
(iv) \( (\sqrt{2}, \sqrt[4]{2}) \)
Answer
For a linear equation a point will be its solution, if it satisfies the equation.So put the points directly in the equation given, if the equation is satisfied, it is a solution or else it is not. Given Equation: \( x-2 y=4\)
Put \( {x}=\sqrt{2} \)
And
In the equation \( x-2 y=4 \)
\(\sqrt{2}-2 * \sqrt[4]{2}=4\)
\(\sqrt{2}-\sqrt[8]{2}=4\)
\(\sqrt{2}(1-8)=4\)
\(-\sqrt[7]{2} \neq 4\)
Therefore,
\( (\sqrt{2}, \sqrt[4]{2}) \) is n't a solution of the given equation
(v) \( (1,1) \)
Answer
For a linear equation a point will be its solution, if it satisfies the equation.So put the points directly in the equation given, if the equation is satisfied, it is a solution or else it is not. Given Equation: \( x-2 y=4\)
Put \( x=1 \)
And
\(y=1\)
In the equation \( x-2 y=4 \)
\(1-2 * 1=4\)
\(-1 \neq 4\)
Therefore, \( (1,1) \) isn't a solution of the given equation.
4. Find the value of \( k \), if \( x=2, y=1 \) is a solution of the equation \( 2 {x}+3 {y}={k} \)
Answer
The Given equation is \( 2 {x}+3 {y}={k} \)The solution of the given equation is:
\( {x}=2 \) and \( {y}=1 \), this means that the equation will satisfy these points.
Now,
After putting the value of \( x \) and \( y \) in the equation, we get
\(2 \times 2+3 \times 1=k\)
\(k=4+3\)
\(k=7\)
