Class 9 maths chapter 4 exercise 4.3 solutions || exercise 4.3 class 9 maths || maths chapter 4 exercise 4.3 class 9 || linear equations in two variables class 9 extra questions || chapter 4 maths class 9 exercise 4.3 question 4 || ncert solutions for class 9 maths ch 4 ex 4.3 || class 9 chapter 4 exercise 4.3 maths || ncert maths class 9 chapter 4 exercise 4.3 question 4 || class 9 maths chapter 4 exercise 4.3 solutions || maths class 9 exercise 4.3
Explore clear, step-by-step solutions for Class 9 Maths Chapter 4, Exercise 4.3, focused on Linear Equations in Two Variables. This exercise helps students deepen their understanding of how to represent linear equations graphically. By plotting points and drawing lines on a Cartesian plane, learners gain insight into the visual nature of linear equations and how each equation forms a straight line. Engaging with Exercise 4.3 strengthens students’ skills in choosing appropriate values, finding corresponding solutions and interpreting graphs—laying a strong foundation for more complex algebraic and geometric concepts in higher classes.

math chapter 4 class 9 exercise 4.3 || exercise 4.3 class 9 maths || maths chapter 4 exercise 4.3 class 9 || linear equations in two variables class 9 extra questions || chapter 4 maths class 9 exercise 4.3 question 4 || ncert solutions for class 9 maths ch 4 ex 4.3 || class 9 chapter 4 exercise 4.3 maths || ncert maths class 9 chapter 4 exercise 4.3 question 4 || class 9 maths chapter 4 exercise 4.3 solutions || maths class 9 exercise 4.3
Exercise 4.3
1. Draw the graph of each of the following linear equations in two variables:
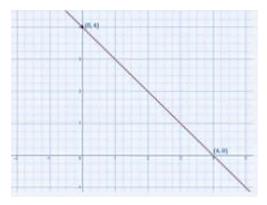
(i) \( x+y=4 \)
Answer
Given equation: \( x+y=4 \)Put \( x=0 \) hence, \( y=4 \) Put \( x=4 \) hence, \( y=0 \)
We write the values of \( x \) and \( y \) satisfying the equation in a table:
\(\begin{array}{|l|l|l|}
\hline X & 0 & 4 \\ \hline
Y & 4 & 0 \\
\hline
\end{array}\)
Now we have two points \( {A}(0,4) \) and \( {B}(4,0) \). We are going to plot these points on graph and then join the points to find the line satisfying the equation.
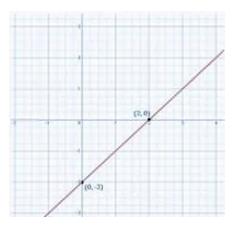
(ii) \( x-y=2 \)
Answer
Give Equation:\(x-y=2\)
Put \( x=0 \) hence, \( y=-2 \)
Put \( x=2 \) hence, \( y=0 \)
We write the values of \( x \) and \( y \) satisfying the equation in a table
\(\begin{array}{|l|l|l|}
\hline X & 0 & 2 \\
\hline Y & -2 & 0 \\
\hline
\end{array}\)
Now we have two points \( {A}(0,-2) \) and \( {B}(2,0) \) to plot on the graph. Plot these points and join them with a line to obtain the graph of equation.
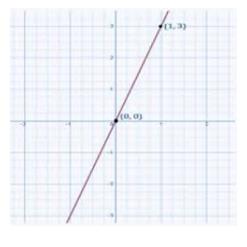
(iii) \( y=3 x \)
Answer
Given Equation:\(y=3 x\)
Put \( x=0 \) hence, \( y=0 \)
Put \( x=1 \) hence, \( y=3 \)
We write values of \( x \) and \( y \) satisfying the equation in a table
\(\begin{array}{|l|l|l|}
\hline x & 0 & 1 \\
\hline y & 0 & 3 \\
\hline
\end{array}\)
Now we have two points \( {A}(0,0) \) and \( {B}(1,3) \) to plot on graph. Join these points together to obtain graph of the equation.
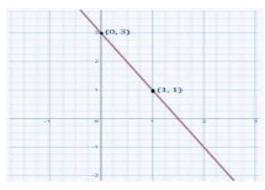
(iv) \( 3=2 x+y \)
Answer
Given equation:\(3=2 x+y\)
Put \( x=0 \) hence, \( y=3 \)
Put \( {x}=1 \) hence, \( {y}=1 \)
We write the values of \( x \) and \( y \) satisfying the equation in a table.
\(\begin{array}{|l|l|l|}
\hline x & 0 & 1 \\
\hline y & 3 & 1 \\
\hline
\end{array}\)
Now we have two points \( {A}(0,3) \) and \( {B}(1,1) \) to plot on the graph. Join the points and the line obtained will be the graph of the equation.
Note: You have to take at least two points to draw a graph.
2. Give the equations of two lines passing through \( (2,14) \). How many more such lines are there, and why?
Answer
Here,\( {x}=2 \) and \( {y}=14 \)
Hence,
\(x+y=16\)
Also,
\(y=7 x\)
\(y-7 x=0\)
Therefore,
The equations of two lines passing through \( (2,14) \) are:
\(x+y=16\)
And,
\(y-7 x=0\)
There would be infinite such lines because infinite number of lines can pass through a given point.
We can also see this graphically:
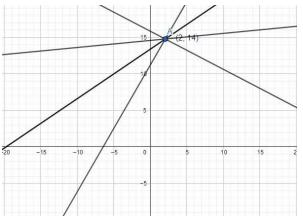
From a single point there can be infinite number of lines that can pass.
3. If the point \( (3,4) \) lies on the graph of the equation \( 3 y=a x+ 7 \), find the value of a.
Answer
The point \( (3,4) \) lies on the graph of the equation \( 3 y=a x+7 \)Therefore,
Put \( x=3 \) and \( y=4 \) in the equation,
\(3 y=a x+7\)
Hence,
\(3 \times 4=a \times 3+7\)
\(12=3 a+7\)
\(3 a=12-7\)
\(3 a=5\)
\(a=\frac{ 5 }{ 3 }\)
math chapter 4 class 9 exercise 4.3 || exercise 4.3 class 9 maths || maths chapter 4 exercise 4.3 class 9 || linear equations in two variables class 9 extra questions || chapter 4 maths class 9 exercise 4.3 question 4 || ncert solutions for class 9 maths ch 4 ex 4.3 || class 9 chapter 4 exercise 4.3 maths || ncert maths class 9 chapter 4 exercise 4.3 question 4 || class 9 maths chapter 4 exercise 4.3 solutions || maths class 9 exercise 4.3
4. The taxi fare in a city is as follows: For the first kilo-meter the fare is Rs 8 and for the subsequent distance it is Rs 5 per km. Taking the distance covered as \(x\) km and total fare as Rs \(y\), write a linear equation for this information, and draw its graph.
Answer
Total fare of the taxi \( =y \)Total distance covered \( ={x} \)
Fare for the subsequent distance after 1 st kilometer \( = \) Rs 5
Fare for \( 1^{\text {st}} \) kilometer \( = \) Rs 8
As per the question,
Total fare \( = \) fare of \( 1 \text {st } \mathrm{km} \ + \) Fare of subsequent \(\mathrm{km} \ \times \) Distance covered
Now for first km, Fare \( = \) Rs. 8 For 2nd km, Fare \( =8+5 \) For 3rd km, Fare \( =8+2 \times 5 \) And so on, let total fare by y and distance travel be \(x \). We can see that \(x\) is one less than the number of km travelled in total. So, \( {y}=8+ 5({x}-1)=8+5 {x}-5=5 {x}+3 \)
Now for plotting graph of the given linear equation, we would need different points,
\(\begin{array}{|l|l|l|}
\hline x & 0 & 1 \\
\hline y & 3 & 8 \\
\hline
\end{array}\)
So the two points two plot are \( {A}(0,3) \) and \( {B}(1,8) \). By joining these points, we will get the graph of the linear equation.
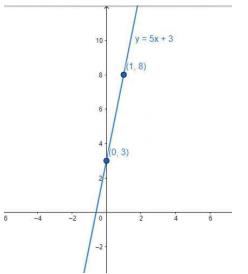
Note: AS it involves Cost on y-axis So please ignore the negative portion of the graph for calculation purpose.
5. From the choices given below, choose the equation whose graphs are given in Figure 4.6 and Figure 4.7
For Fig 4.6
(i)
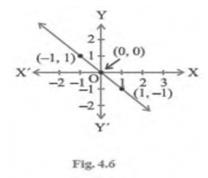
\( y=x \)

\( y=x \)
Answer
In figure 4.6,Points plotted are \( (0,0),(-1,1) \) and \( (1,-1) \)
Now let us take equations one by one.
\( y=x \).
at \( x=0, y=0 \) at \( x=-1, y=-1 \ [(-1,1) \) point is not satisfied\( ] \) Therefore, the equation does not follow the graph.
(ii)

\( x+y=0 \)

\( x+y=0 \)
Answer
In figure 4.6,Points plotted are \( (0,0),(-1,1) \) and \( (1,-1) \)
Now let us take equations one by one.
\( x+y=0 \)
at \( {x}=0, {y}=0 \) at \( {x}=-1, {y}=1 \) at \( {x}=1, {y}=-1 \) All the points are satisfied and Hence, the equation follows the graph.
(iii)

\( y=2 x \)

\( y=2 x \)
Answer
In figure 4.6,Points plotted are \( (0,0),(-1,1) \) and \( (1,-1) \)
Now let us take equations one by one.
\( y=2 x \)
at \( x=-1, y=-2 \ [(-1,1) \) point is not satisfied\( ] \) Therefore, the equation does not follow the graph.
math chapter 4 class 9 exercise 4.3 || exercise 4.3 class 9 maths || maths chapter 4 exercise 4.3 class 9 || linear equations in two variables class 9 extra questions || chapter 4 maths class 9 exercise 4.3 question 4 || ncert solutions for class 9 maths ch 4 ex 4.3 || class 9 chapter 4 exercise 4.3 maths || ncert maths class 9 chapter 4 exercise 4.3 question 4 || class 9 maths chapter 4 exercise 4.3 solutions || maths class 9 exercise 4.3
(iv)

\( 2+3 y=7 x \)

\( 2+3 y=7 x \)
Answer
In figure 4.6,Points plotted are \( (0,0),(-1,1) \) and \( (1,-1) \)
Now let us take equations one by one.
\( 2+3 y=7 x \)
at \( x=0, y=-\frac{2}{3} \ [(0,0) \) point is not satisfied\( ] \) Therefore, the equation does not follow the graph.
For Fig 4.7
(i)
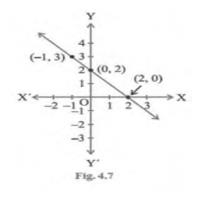
\( y=x+2 \)

\( y=x+2 \)
Answer
In figure 4.7, points are \( (-1,3),(0,2) \) and \( (2,0) \)Hence,
\( y=x+2 \)
at \( x=-1, y=1 \ [(-1,3) \) point is not satisfied\( ] \) Therefore, the equation does not follow the graph.
(ii)

\( y=x-2 \)

\( y=x-2 \)
Answer
In figure 4.7, points are \( (-1,3),(0,2) \) and \( (2,0) \)Hence,
\( y=x-2 \)
at \( x=-1, y=-3 \ [(-1,3) \) point is not satisfied\( ] \) Therefore, the equation does not follow the graph.
math chapter 4 class 9 exercise 4.3 || exercise 4.3 class 9 maths || maths chapter 4 exercise 4.3 class 9 || linear equations in two variables class 9 extra questions || chapter 4 maths class 9 exercise 4.3 question 4 || ncert solutions for class 9 maths ch 4 ex 4.3 || class 9 chapter 4 exercise 4.3 maths || ncert maths class 9 chapter 4 exercise 4.3 question 4 || class 9 maths chapter 4 exercise 4.3 solutions || maths class 9 exercise 4.3
(iii)

\( y=-x+2 \)

\( y=-x+2 \)
Answer
In figure 4.7, points are \( (-1,3),(0,2) \) and \( (2,0) \)Hence,
\( y=-x+2 \)
at \( x=-1, y=3 \) at \( x=0, y=2 \) at \( x=2, y=0 \) Therefore, all the points are satisfied and the equation follows the graph.
(iv)

\( x+2 y=6 \)

\( x+2 y=6 \)
Answer
In figure 4.7, points are \( (-1,3),(0,2) \) and \( (2,0) \)Hence,
\( x+2 y=6 \)
at \(x = - 1, y = \frac{7}{2} \ [(-1, 3)\) point is not satisfied\(] \) Hence, the equation does not follow the graph.
6. If the work done by a body on application of a constant force is directly proportional to the distance travelled by the body, express this in the form of an equation in two variables and draw the graph of the same by taking the constant force as 5 units. Also read from the graph the work done when the distance travelled by the body is (i) 2 units (ii) 0 unit
Answer
Let the distance travelled be \(x\) by the body and \(y\) be the work done by the forceGiven: \( {y} \propto {x} \)
To equate the proportional, we need a constant.
Hence, \( {y}={k}x \) where \(k\) is a constant
Here, it is given 5
Hence,
\( y=5 x \)
According to question,
(i) When \( {x}=2 \) units then \( {y}=5 \times 2=10 \) units
(ii) When \( {x}=0 \) unit then \( {y}=5 \times 0=0 \) unit
\(\begin{array}{|l|l|l|}
\hline x & 2 & 0 \\
\hline y & 10 & 0 \\
\hline
\end{array} \)
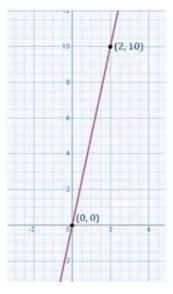
math chapter 4 class 9 exercise 4.3 || exercise 4.3 class 9 maths || maths chapter 4 exercise 4.3 class 9 || linear equations in two variables class 9 extra questions || chapter 4 maths class 9 exercise 4.3 question 4 || ncert solutions for class 9 maths ch 4 ex 4.3 || class 9 chapter 4 exercise 4.3 maths || ncert maths class 9 chapter 4 exercise 4.3 question 4 || class 9 maths chapter 4 exercise 4.3 solutions || maths class 9 exercise 4.3
7. Yamini and Fatima, two students of Class IX of a school, together contributed Rs 100 towards the Prime Minister's Relief Fund to help the earthquake victims. Write a linear equation which satisfies this data. (You may take their contributions as Rs \(x\) and Rs \(y\)) Draw the graph of the same.
Answer
Let the amount contributed by Yamini be \(x\) and amount contributed by Fatima be \(y\)Now, according to question,
\(x+y=100\)
This will be the required linear equation. Now for plotting this on graph, we would need different points through which this graph passes.
When \( {x}=0 \) then \( {y}=100 \)
When \( x=50 \) then \( y=50 \)
When \( {x}=100 \) then \( {y}=0 \)
\(\begin{array}{|l|l|l|l|}
\hline X & 0 & 50 & 100 \\
\hline Y & 100 & 50 & 0 \\
\hline
\end{array}\)
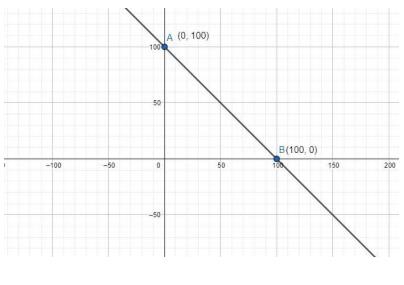
8. In countries like USA and Canada, temperature is measured in Fahrenheit, whereas in countries like India, it is measured in Celsius. Here is a linear equation that converts Fahrenheit to Celsius:
(i) Draw the graph of the linear equation above using Celsius for \(x\) -axis and Fahrenheit for \( y \)-axis.
Answer
Given:\({F}={ }_{5}^{9} {C}+32\)
When \( {C}=0 \) then \( {F}=32 \),
And
When \( {C}=-10 \) then
\(F=9(-2)+32=-18+32=14\)
Now plotting the two points \( (0,32) \) and \( (-10,14) \)
\(\begin{array}{|l|l|l|}
\hline C & 0 & -10 \\
\hline F & 32 & 14 \\
\hline
\end{array}\)
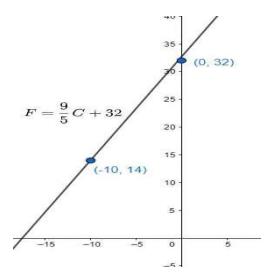
(ii) If the temperature is \( 30^{\circ} {C} \), what is the temperature in Fahrenheit?
Answer
Putting the value of \( {C}=30 \) in \( {F}=\left(\frac{9}{5}\right) {C}+32 \), we get\({F}=\frac{9}{5} \times 30+32\)
\({F}=54+32\)
\({F}=86\)
(iii) If the temperature is \( 95^{\circ} {F} \), what is the temperature in Celsius?
Answer
Putting the value of \( {F}=95 \) in \( {F}=\left(\frac{9}{5}\right) {C}+32 \), we get\(95=\left(\frac{9}{5}\right) C+32\)
\(\left(\frac{9}{5}\right) C=95-32\)
\(C=63 \times \frac{5}{9}\)
\(C=35\)
(iv) If the temperature is \( 0^{\circ} {C} \), what is the temperature in Fahrenheit and if the temperature is \( 0^{0} {F} \), what is the temperature in Celsius?
Answer
After putting the value of \( {F}=0 \) in\(F=\left(\frac{9}{5}\right) C+32\)
We get:
\(0=\left(\frac{9}{5}\right) C+32\)
\(\left(\frac{9}{5}\right)=-32\)
\(C=-32 \times \frac{5 }{ 9}\)
\(C=-\frac{160}{9}\)
Putting the value of \( {C}=0 \) in
\({F}=\left(\frac{9}{5}\right) \times C+32\)
We get:
\({F}=\left(\frac{9}{5}\right) \times 0+32\)
\({F}=32\)
(v) Is there a temperature which is numerically the same in both Fahrenheit and Celsius? If yes, find it.
Answer
We have to find when \( {F}={C} \)Hence
After putting \( {F}={C} \) in
We get:
\( {F}=\left(\frac{9}{F}\right) {C}+32 \)
F \( -\frac{9}{F} \times F=32 \)
\( \frac{5 F-9 F}{5}=32 \)
\( \frac{-4}{5} {F}=32 \)
\( {F}=32 \)
\( {F}=-40 \)
Therefore, at value \(-40 \),
Fahrenheit and Celsius both are numerically the same.

