Rd sharma class 9 Lines and Angles || ex 6.1 class 9 maths ncert solutions || class 9 maths chapter 6 exercise 6.1 || ncert solutions for class 9 maths chapter 6 exercise 6.1
Explore clear, step-by-step solutions for Class 9 Maths Chapter 6, Exercise 6.1, focused on Lines and Angles. This exercise builds upon students’ understanding of fundamental geometric concepts such as intersecting lines, adjacent angles, and linear pairs. Through logical reasoning and structured problem-solving, learners gain clarity on how angles form and relate when lines interact. Exercise 6.1 helps students develop the ability to recognize and apply basic angle relationships, such as complementary, supplementary, and vertically opposite angles. By working through these problems, students sharpen their analytical skills and lay a strong conceptual foundation for advanced geometry topics.

rd sharma class 9 Lines and Angles || ex 6.1 class 9 maths ncert solutions || class 9 maths chapter 6 exercise 6.1 || ncert solutions for class 9 maths chapter 6 exercise 6.1
Exercise 6.1
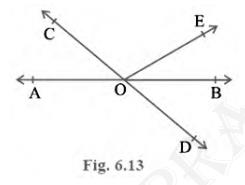
1. In Fig. 6.13, lines AB and CD intersect at O. If \( \angle
\mathrm{AOC}+\angle \mathrm{BOE}=70^{\circ} \) and \( \angle
\mathrm{BOD}=40^{\circ} \), find \( \angle \mathrm{BOE} \) and
reflex \( \angle COE\) .

Answer
It is given: \( \angle \mathrm{AOC}+\angle \mathrm{BOE}=70^{\circ}
\)And, \( \angle \mathrm{BOD}=40^{\circ} \)
Now, according to the question,
\( \angle \mathrm{AOC}+\angle \mathrm{BOE}+\angle \mathrm{COE}=180^{\circ} \) (Sum of linear pair is always \(180^{\circ}\))
\( \Rightarrow 70^{\circ}+\angle \mathrm{COE}=180^{\circ} \)
\( \Rightarrow \angle \mathrm{COE}=110^{\circ}\)
And,
\( \angle \mathrm{COE}+\angle \mathrm{BOD}+\angle \mathrm{BOE}=180^{\circ} \) (Sum of linear pair is always \( 180^{\circ} \))
putting the value of \( \angle \mathrm{COE} \), we get,
\( 110^{\circ}+40^{\circ}+\angle B O E=180^{\circ} \)
\( 150^{\circ}+\angle \mathrm{BOE}=180^{\circ} \)
\( \therefore \angle \mathrm{BOE}=30^{\circ} \)
Now, reflex \( \angle \mathrm{COE}=360^{\circ}-\angle \mathrm{COE} \)
\( \Rightarrow \) reflex \( \angle \mathrm{COE}=360^{\circ}-110^{\circ} \)
\( \therefore \) reflex \( \angle \mathrm{COE}=250^{\circ} \)
Note: Reflex here means the reflex angles which are greater than \( 180^{\circ} \) but less than \( 360^{\circ} \).
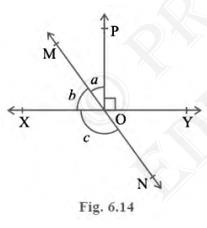
2. In Fig. 6.14, lines XY and MN intersect at O. If \( \angle
\mathrm{POY}= 90^{\circ} \) and \( \mathrm{a}: \mathrm{b}=2: 3 \),
find \(\mathrm{b}\).

Answer
Given: \( \angle \mathrm{POY}=90^{\circ} \)\( \mathrm{a}: \mathrm{b}=2: 3 \)
Now, according to the question,
\( \angle \mathrm{POY}+\mathrm{a}+\mathrm{b}=180^{\circ} \quad \) (Angles made on a straight line are supplementary or sum of angles equals to \( 180^{\circ} \))
\(90^{\circ}+a+b=180^{\circ}\)
\(a+b=90^{\circ}\quad \ldots\ldots\text{(1)}\)
Now \( a: b=2: 3 \quad \ldots\ldots\text{(2)}\)
Let a be \(2 x\) and b be \(3 x\)
So putting this value in eq(1),
\(2 x+3 x=90^{\circ}\)
\(5x=90^{\circ}\)
\(x=18^{\circ}\)
Hence,
\(a=2 \times 18^{\circ}=36^{\circ}\)
And,
\(\mathrm{b}=3 \times 18^{\circ}=54^{\circ}\)
And,
\(\mathrm{b}+\mathrm{c}=180^{\circ} \text { (Linear pair) }\)
\(54^{\circ}+\mathrm{c}=180^{\circ}\)
\(\mathrm{c}=126^{\circ}\)
rd sharma class 9 Lines and Angles || ex 6.1 class 9 maths ncert solutions || class 9 maths chapter 6 exercise 6.1 || ncert solutions for class 9 maths chapter 6 exercise 6.1
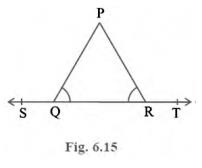
3. In Fig. 6.15, \( \angle \mathrm{PQR}=\angle \mathrm{PRQ} \),
then prove that \( \angle \mathrm{PQS}=\angle\mathrm{PRT}\).

Answer

Given: \( \angle \mathrm{PQR}=\angle \mathrm{PRQ} \)
To prove: \( \angle \mathrm{PQS}=\angle \mathrm{PRT} \)
Proof:
Now,
\( \angle \mathrm{PQR}+\angle \mathrm{PQS}=180^{\circ} \quad \) (Angles on a straight line are supplementary)
\(\Rightarrow \angle \mathrm{PQR}=180^{\circ}-\angle \mathrm{PQS}\quad \ldots\ldots\text{(i)}\)
Similarly,
\( \angle \mathrm{PRQ}+\angle \mathrm{PRT}=180^{\circ} \) (Angles on a straight line are supplementary)
\(\Rightarrow \angle \mathrm{PRQ}=180^{\circ}-\angle \mathrm{PRT}\quad \ldots\ldots\text{(ii)}\)
Now, \( \angle \mathrm{PQR}=\angle \mathrm{PRQ} \) (Given)
Therefore, (i) and (ii) will be equal \( 180^{\circ}-\angle \mathrm{PQS}=180^{\circ}-\angle \mathrm{PRT} \)
\(\angle \mathrm{PQS}=\angle \mathrm{PRT}\)
Hence, Proved.
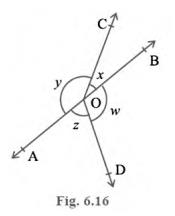
4. In Fig. 6.16, if \( {x}+{y}=\mathrm{w}+{z} \), then prove that
AOB is a line.

Answer
Given: \( x+y=w+z \)To prove: AOB is a line or \( {x}+{y}=180^{\circ} \) (Linear pair)
Proof:
Now, according to the question,
\(x+y+w+z=360^{\circ} \text { (Angles at a point) }\)
\((x+y)+(w+z)=360^{\circ}\)
(Given, \( x+y=w+z) \)
\(2(x+y)=360^{\circ}\)
\((x+y)=180^{\circ}\)
Therefore, \( x+y \) makes a linear pair.
And, \( A O B \) is a straight line
Hence, Proved.
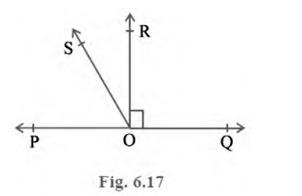
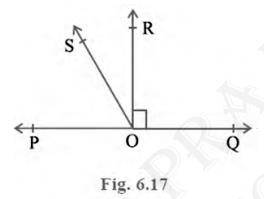
5. In Fig. 6.17, POQ is a line. Ray OR is perpendicular to line
PQ. OS is another ray lying between rays OP and OR. Prove that \(
\angle \mathrm{ROS} =\frac{1}{2}(\angle \mathrm{QOS}-\angle
\mathrm{POS}) \).

Answer
Given: OR is perpendicular to line PQ
To prove: \( \angle \mathrm{ROS}=(\angle \mathrm{QOS}-\angle \mathrm{POS}) \)
Proof:
Now, according to the question,
\( \angle \mathrm{POR}=\angle \mathrm{ROQ}=90^{\circ}(\because \mathrm{OR} \) is perpendicular to line \( \mathrm{PQ}) \)
\(\angle \mathrm{QOS}=\angle \mathrm{ROQ}+\angle \mathrm{ROS}=90^{\circ}+\angle \mathrm{ROS}\quad \ldots\ldots\text{(i)}\)
We can write,
\(\angle \mathrm{POS}=\angle \mathrm{POR}-\angle \mathrm{ROS}=90^{\circ}-\angle \mathrm{ROS}\quad \ldots\ldots\text{(ii)} \)
Subtracting (ii) from (i), we get
\(\angle \mathrm{QOS}-\angle \mathrm{POS}=90^{\circ}+\angle \mathrm{ROS}-\left(90^{\circ}-\angle \mathrm{ROS}\right)\)
\(\angle \mathrm{QOS}-\angle \mathrm{POS}=90^{\circ}+\angle \mathrm{ROS}-90^{\circ}+\angle \mathrm{ROS}\)
\(\angle \mathrm{QOS}-\angle \mathrm{POS}=2 \angle \mathrm{ROS}\)
\(\angle \mathrm{ROS}=\frac{1}{2}(\angle \mathrm{QOS})-(\angle \mathrm{POS})\)
Hence, proved
6. It is given that \( \angle X Y Z=64^{\circ} \) and \( X Y \)
is produced to point \( P \). Draw a figure from the given
information. If ray \( Y Q \) bisects \( \angle Z Y P \), find \(
\angle {XYQ} \) and reflex \( \angle {QYP} \).
Answer
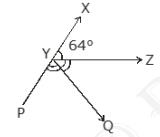
Given: \( \angle X Y Z=640 \)
\(YQ\) bisects \( \angle {ZYP} \), therefore \( \angle {QYP}=\angle {QYZ} \)
\( \angle X Y Z+\angle Z Y P=180^{\circ} \) (Sum of angles made on a straight line \(=180^{\circ}\))
\(64^{\circ}+\angle {ZYP}=180^{\circ}\)
\(\angle {ZYP}=116^{\circ}\)
And,
\(\angle {ZYP}=\angle {ZYQ}+\angle {QYP}\)
\(\angle {ZYQ}=\angle {QYP} \ ({YQ} \text { bisects } \angle {ZYP})\)
\(\angle {ZYP}=2 \angle {ZYQ}\)
\(2 \angle {ZYQ}=116^{\circ}\)
\(\angle {ZYQ}=58^{\circ}=\angle {QYP}\)
Now,
\(\angle {XYQ}=\angle {XYZ}+\angle {ZYQ}\)
\(\angle {XYQ}=64^{\circ}+58^{\circ}\)
\(\angle {XYQ}=122^{\circ}\)
And,
Reflex of \( \angle {QYP}=180^{\circ}+\angle {XYQ} \)
\(\angle {QYP}=180^{\circ}+122^{\circ}\)
\(\angle {QYP}=302^{\circ}\)

