Class 9 ncert exercise 7.4 || rd sharma class 9 triangle || ncert class 9 exercise 7.4 || exercise 7.4 maths class 9 || chapter 7 maths class 9 exercise 7.4 || chapter 7 exercise 7.4 class 9 || class 9 maths chapter 7 exercise 7.4 solutions || maths chapter 7 class 9 exercise 7.4 || exercise 7.4 class 9 maths
Explore clear, step-by-step solutions for Class 9 Maths Chapter 7, Exercise 7.4, which deals with applying the concept of triangle congruence in real-world geometric contexts. This exercise builds on the congruence rules students have learned, especially in practical applications such as proving properties of triangles and constructing geometric figures. By solving problems that involve conditions like SSS, SAS, ASA, and RHS, students sharpen their logical thinking and proof-writing skills. Exercise 7.4 reinforces the understanding of congruence as a tool to justify equal lengths and angles in geometrical figures, thereby preparing learners for advanced topics in geometry, such as trigonometry and coordinate geometry.

class 9 ncert exercise 7.4 || rd sharma class 9 triangle || ncert class 9 exercise 7.4 || exercise 7.4 maths class 9 || chapter 7 maths class 9 exercise 7.4 || chapter 7 exercise 7.4 class 9 || class 9 maths chapter 7 exercise 7.4 solutions || maths chapter 7 class 9 exercise 7.4 || exercise 7.4 class 9 maths
Exercise 7.4
1. Show that in a right-angled triangle, the hypotenuse is the
longest side.
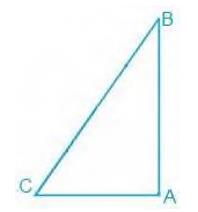

Answer
It is known that \( \mathrm{ABC}\) is a triangle right angled at
\( \mathrm{B}\) .We know that,
\(A+B+C=180^{\circ}\)
Now, if \( \mathrm{B}+\mathrm{C}=90^{\circ} \) then A has to be \( 90^{\circ} \).
Since \( \mathrm{A}\) is the largest angle of the triangle, the side opposite to it must be the largest.
\( \mathrm{So}, \mathrm{AB} \) is the hypotenuse which will be the largest side of the above right-angled triangle i.e. \( \triangle \mathrm{ABC} \).
2. In Fig. 7.48, sides \( A B \) and \( A C \) of \( \triangle A
B C \) are extended to points \( P \) and \(Q\) respectively.
Also, \( \mathrm{PBC} < \mathrm{QCB} \). Show that \(
\mathrm{AC} > \mathrm{AB} \).
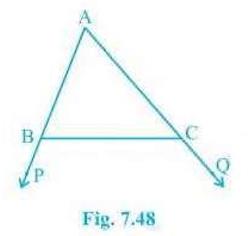

Answer
It is given that \( \mathrm{PBC} < \mathrm{QCB} \)We know that \( \mathrm{ABC}+\mathrm{PBC}=180^{\circ} \)
So, \( \mathrm{ABC}=180^{\circ}-\mathrm{PBC} \)
Also,
\( \mathrm{ACB}+\mathrm{QCB}=180^{\circ} \)
Therefore, \( \mathrm{ACB}=180^{\circ}-\mathrm{QCB} \)
Now, since \( \mathrm{PBC} < \mathrm{QCB} \),
\( \therefore \mathrm{ABC} > \mathrm{ACB} \)
Hence, \( \mathrm{AC} > \mathrm{AB} \) as sides opposite to the larger angle is always larger.
class 9 ncert exercise 7.4 || rd sharma class 9 triangle || ncert class 9 exercise 7.4 || exercise 7.4 maths class 9 || chapter 7 maths class 9 exercise 7.4 || chapter 7 exercise 7.4 class 9 || class 9 maths chapter 7 exercise 7.4 solutions || maths chapter 7 class 9 exercise 7.4 || exercise 7.4 class 9 maths
3. In Fig. 7.49, \(B < A\) and \(C < D\). Show that \(AD
< BC\).
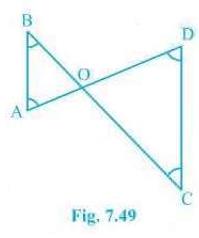

Answer
In the question, it is mentioned that angles \( B \) and angle \(
C \) is smaller than angles \( \mathrm{A}\) and \( \mathrm{D}\)
respectively i.e. \( \mathrm{B} < \mathrm{A} \) and \(
\mathrm{C} < \mathrm{D} \).Now,
Since the side opposite to the smaller angle is always smaller
\( \mathrm{AO} < \mathrm{BO} \ldots\)(i)
And \( \mathrm{OD} < \mathrm{OC}\ldots\)(ii)
By adding equation (i) and equation (ii) we get
\(\mathrm{AO}+\mathrm{OD} < \mathrm{BO}+\mathrm{OC}\)
So, \( \mathrm{AD} < \mathrm{BC} \)
4. \( \mathrm{AB}\) and \( \mathrm{CD}\) are respectively the
smallest and longest sides of a quadrilateral \( \mathrm{ABCD}\)
(see Fig. 7.50).
Show that \( \mathrm{A} > \mathrm{C} \) and \( \mathrm{B} > \mathrm{D} \).
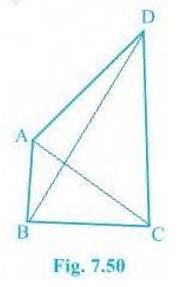
Show that \( \mathrm{A} > \mathrm{C} \) and \( \mathrm{B} > \mathrm{D} \).

Answer
In \( \triangle \mathrm{ABD} \), we see that\(\mathrm{AB} < \mathrm{AD} < \mathrm{BD}\)
So, \( \mathrm{ADB} < \mathrm{ABD}\ldots\)(i)
(Since angle opposite to longer side is always larger)
Now, in \( \triangle B C D \),
\(\mathrm{BC} < \mathrm{DC} < \mathrm{BD}\)
Hence, it can be concluded that
\(\mathrm{BDC} < \mathrm{CBD}\ldots\)(ii)
Now, by adding equation (i) and equation (ii) we get,
\(\mathrm{ADB}+\mathrm{BDC} < \mathrm{ABD}+\mathrm{CBD}\)
\(\mathrm{ADC} < \mathrm{ABC}\)
\(\mathrm{B} > \mathrm{D}\)
Similarly, In triangle \( A B C \),
\( \mathrm{ACB} < \mathrm{BAC} \ldots\)(iii)
(Since the angle opposite to the longer side is always larger)
Now, In \( \triangle \mathrm{ADC} \),
\( \mathrm{DCA} < \mathrm{DAC}\ldots\) (iv)
By adding equation (iii) and equation (iv) we get,
\(\mathrm{ACB}+\mathrm{DCA} < \mathrm{BAC}+\mathrm{DAC}\)
\(\Rightarrow \mathrm{BCD} < \mathrm{BAD}\)
\(\therefore \mathrm{A} > \mathrm{C}\)
5. In Fig 7.51, \( \mathrm{PR} > \mathrm{PQ}\) and \(
\mathrm{PS}\) bisect \( \mathrm{QPR}\). Prove that \( \mathrm{PSR}
> \mathrm{PSQ}\).
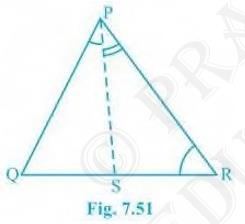

Answer
It is given that \( P R > P Q \) and \( P S \) bisects \( Q P R
\)Now we will have to prove that angle PSR is smaller than \( \mathrm{PSQ}\) i.e. \( \mathrm{PSR} > \mathrm{PSQ}\)
Proof:
\(\mathrm{QPS}=\mathrm{RPS}\ldots\)(ii) (As PS bisects \(\angle \mathrm{QPR}\))
\(\mathrm{PQR} > \mathrm{PRQ}\ldots\)(i)
(Since \( \mathrm{PR} > \mathrm{PQ} \) as angle opposite to the larger side is always larger)
\(\mathrm{PSR}=\mathrm{PQR}+\mathrm{QPS}\ldots\)(iii)
(Since the exterior angle of a triangle equals to the sum of opposite interior angles)
\( \mathrm{PSQ} = \mathrm{PRQ} + \mathrm{RPS}\)
(As the exterior angle of a triangle equals to the sum of opposite interior angles)
By adding (i) and (ii)
\(\mathrm{PQR}+\mathrm{QPS} > \mathrm{PRQ}+\mathrm{RPS}\)
Thus, from (i), (ii), (iii) and (iv), we get
\( \mathrm{PSR} > \mathrm{PSQ}\)
6. Show that of all line segments drawn from a given point not on
it, the perpendicular line segment is the shortest.
Answer
First, let "\( l \)" be a line segment and "\( \mathrm{B}\)" be a
point lying on it. A line \( \mathrm{AB}\) perpendicular to \( l
\) is now drawn. Also, let \( \mathrm{C}\) be any other point on
\( l \). The diagram will be as follows: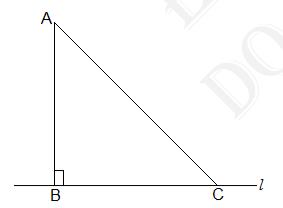
To prove:
\(\mathrm{AB} < \mathrm{AC}\)
Proof:
In \( \triangle \mathrm{ABC}, \mathrm{B}=90^{\circ} \)
Now, we know that
\(\mathrm{A}+\mathrm{B}+\mathrm{C}=180^{\circ}\)
\(\therefore \mathrm{A}+\mathrm{C}=90^{\circ}\)
Hence, \( \mathrm{C}\) must be an acute angle which implies \( \mathrm{C} < \mathrm{B} \)
So, \( \mathrm{AB} < \mathrm{AC} \) (As the side opposite to the larger angle is always larger)

