Chapter 7 maths class 9 exercise 7.5 || ncert class 9 exercise 7.5 || exercise 7.5 maths class 9 || maths chapter 7 class 9 exercise 7.5 || exercise 7.5 class 9 maths || chapter 7 exercise 7.5 class 9 || class 9 ncert exercise 7.5
Explore clear, step-by-step solutions for Class 9 Maths Chapter 7, Exercise 7.5, which focuses on deepening students’ understanding of triangle congruence through logical reasoning and practical application. This exercise emphasizes how the congruence criteria — such as SSS, SAS, ASA, and RHS — can be used to prove important properties of triangles and related geometric figures. By working through these problems, students develop confidence in writing geometric proofs, enhance their analytical skills, and learn to apply congruence rules in meaningful contexts. Exercise 7.5 not only strengthens foundational geometry concepts but also lays the groundwork for future studies in constructions, trigonometry, and coordinate geometry.

chapter 7 maths class 9 exercise 7.5 || ncert class 9 exercise 7.5 || exercise 7.5 maths class 9 || maths chapter 7 class 9 exercise 7.5 || exercise 7.5 class 9 maths || chapter 7 exercise 7.5 class 9 || class 9 ncert exercise 7.5
Exercise 7.5
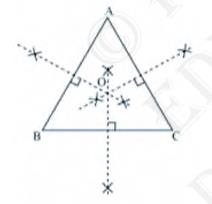
1. \( \mathrm{ABC}\) is a triangle. Locate a point in the
interior of \( \triangle \mathrm{ABC} \) which is equidistant from
all the vertices of \( \triangle \mathrm{ABC} \).
Answer
Circum centre of a triangle is always equidistant from all the
vertices of that particular triangle.Circum centre is the point where perpendicular bisectors of all the sides of the triangle meet together.
In \( \triangle \mathrm{ABC} \), we can find the circum centre by drawing the perpendicular bisectors of sides \( \mathrm{AB}, \mathrm{BC} \), and \( \mathrm{CA}\) of this triangle.
\( \mathrm{O}\) is the point where these bisectors are meeting together.
Therefore,
\( \mathrm{O}\) is the point which is equidistant from all the vertices of \( \triangle A B C \)
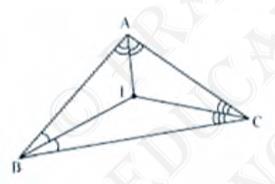
2. In a triangle locate a point in its interior which is
equidistant from all the sides of the triangle.
Answer
The point which is equidistant from all the sides of a triangle is
called the in centre of the triangle.In centre of a triangle is the intersection point of the angle bisectors of the interior angles of that triangle.
Here,
In \( \triangle \mathrm{ABC} \), we can find the in centre of this triangle by drawing the angle bisectors of the interior angles of this triangle.
I am the point where these angle bisectors are intersecting each other.
Therefore,
I is the point equidistant from all the sides of \( \triangle \mathrm{ABC} \).
chapter 7 maths class 9 exercise 7.5 || ncert class 9 exercise 7.5 || exercise 7.5 maths class 9 || maths chapter 7 class 9 exercise 7.5 || exercise 7.5 class 9 maths || chapter 7 exercise 7.5 class 9 || class 9 ncert exercise 7.5
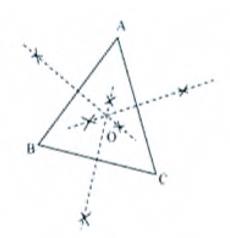
3. In a huge park, people are concentrated at three points (see
Fig. 7.52):

A: Where there are different slides and swings for children,
B: Near which a man-made lake is situated,
C : Which is near to a large parking and exit?
Where should an ice cream parlour be set up so that maximum number of persons can approach it?
(Hint: The parlour should be equidistant from \( A, B \) and \( C \) )

A: Where there are different slides and swings for children,
B: Near which a man-made lake is situated,
C : Which is near to a large parking and exit?
Where should an ice cream parlour be set up so that maximum number of persons can approach it?
(Hint: The parlour should be equidistant from \( A, B \) and \( C \) )
Answer
Maximum number of persons can approach the ice-cream parlour if it
is equidistant from \( \mathrm{A}, \mathrm{B} \) and \(
\mathrm{C}\).Now,
\( \mathrm{A}, \mathrm{B} \) and \( \mathrm{C}\) form a triangle.
In a triangle, the circum centre is the only point that is equidistant from its vertices.
So, the ice-cream parlour should be set up at the circum centre \( \mathrm{O}\) of \( \triangle A B C \) In this situation,
Maximum number of persons can approach it.
We can find circum centre \( \mathrm{O}\) of this triangle by drawing perpendicular bisectors of the sides of this triangle
4. Complete the hexagonal and star shaped Rangolis [see Fig. 7.53
(i) and (ii)] by filling them with as many equilateral triangles
of side 1 cm as you can. Count the number of triangles in each
case. Which has more triangles?
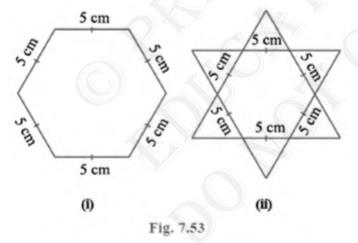

Answer
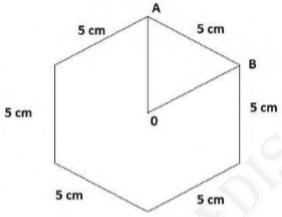
It can be observed that hexagonal-shaped rangolis has 6 equilateral triangles in it
Area of \( \triangle A O B=\frac{\sqrt{3}}{4}\)(Side)\(^{2} \)
\(=\frac{\sqrt{3}}{4}(5)^{2}\)
\(=\frac{\sqrt{3}}{4} \times 25\)
\(=\frac{25 \sqrt{3}}{4} \mathrm{~cm}^{2}\)
Area of hexagonal shaped rangolis \( =6 \times \frac{25 \sqrt{3}}{4} \)
\(=\frac{75 \sqrt{3}}{2} \mathrm{~cm}^{2}\)
Area of equilateral triangle having its side as \( 1 \mathrm{~cm}=\frac{\sqrt{3}}{4}(1)^{2} \)
\(=\frac{\sqrt{3}}{4} \mathrm{~cm}^{2}\)
Number of equilateral triangle of 1 cm side that can be filed in this hexagonal shaped rangolis \( =\frac{\frac{75 \sqrt{3}}{2}}{\frac{\sqrt{3}}{4}}=150 \)
Star shaped rangolis has 12 equilateral triangles of side 5 cm in it Area of star shaped rangolis \( =12 \times \frac{\sqrt{3}}{4} \times(5)^{2} \)
\(=75 \sqrt{3}\)
Number of equilateral triangles of 1 cm side that can be filled in this star shaped rangolis \(=\frac{75 \sqrt{3}}{\frac{\sqrt{3}}{4}}\)
\(=300\)
Therefore, star shaped rangolis has more equilateral triangles in it.

