Number system class 9 extra questions || ncert exemplar class 9 maths solutions chapter 1 || number system questions with solutions pdf || cbse class 9 maths ncert solution up board || class 9 maths chapter 1 exercise 1.2 solutions || ncert exemplar class 9 maths solutions || ncert solutions for class 9 maths
Searching for NCERT Class 9 Maths Chapter 1 Exercise 1.2 solutions? You’re in the right place! This section brings you accurate, step-by-step solutions for all the questions from Chapter 1 – Number Systems, Exercise 1.2. This part of the chapter focuses on representing irrational numbers on the number line using geometrical methods, helping to build a strong conceptual base. Whether you’re preparing for exams or aiming to strengthen your understanding, these solutions are perfect for quick learning and effective revision. With clear explanations this guide will boost your confidence and make tackling irrational numbers a breeze.

number system class 9 extra questions || ncert exemplar class 9 maths solutions chapter 1 || number system questions with solutions pdf || cbse class 9 maths ncert solution up board || class 9 maths chapter 1 exercise 1.2 solutions || ncert exemplar class 9 maths solutions || ncert solutions for class 9 maths
Exercise 1.2
1. State whether the following statements are true or false. Justify your answers.
For example, \( \sqrt{2}=1.414 \ldots \) which can be represented in a number line. All the numbers which can be represented in a number line are real.
number system class 9 extra questions || ncert exemplar class 9 maths solutions chapter 1 || number system questions with solutions pdf || cbse class 9 maths ncert solution up board || class 9 maths chapter 1 exercise 1.2 solutions || ncert exemplar class 9 maths solutions || ncert solutions for class 9 maths
for example: \( 4=\sqrt{2} \) but there is no number whose square root is \(-4\).
For example: \( \sqrt{2} \) is irrational and \( \frac{1}{2} \) is rational and both are real numbers.
Step 1: Let AB be a line of length 2 unit on the number line.
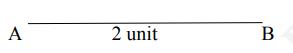
Step 2: At B, draw a perpendicular line BC of length 1 unit and then join CA.
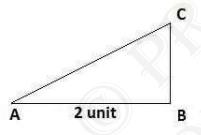
Step 3: Now, ABC is a right angled triangle.
Using Pythagoras theorem,
\(\mathrm{AB}^{2}+\mathrm{BC}^{2} =\mathrm{CA}^{2}\)
\(22+12 =\mathrm{CA}^{2}\)
\(\mathrm{CA}^{2} =25\)
\(\mathrm{CA} =\sqrt{5}\)
Thus, CA is a line of length \( \sqrt{5} \) units.
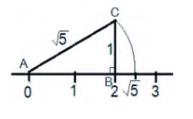
Step 4: Taking CA as a radius and A as the center, construct an arc touching the number line.
The number line gets intersected by the arc at a point which is at \( \sqrt{ } 5 \) distance from 0, as it is a radius of the circle with center A
Thus, \( \sqrt{ } 5 \) is represented on the number line as shown in the figure below.
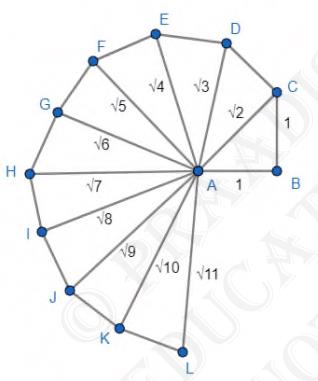
Take a large sheet of paper and construct the 'square root spiral' in the following fashion. Start with a point \(\mathrm{O}\) and draw a line segment \( \mathrm{P}_{1} \mathrm{P}_{2} \) perpendicular to \( \mathrm{OP}_{1} \) of unit length (see Fig. 1.9). Now draw a line segment \( \mathrm{P}_{2} \mathrm{P}_{3} \) perpendicular to \( \mathrm{OP}_{2} \). Then draw a line segment \(\mathrm{P 3 P 4}\) perpendicular to \( \mathrm{OP}_{3} \). Continuing in this manner, you can get the line segment \( \mathrm{Pn}-1 \mathrm{Pn} \) by drawing a line segment of unit length perpendicular to \( \mathrm{OP}_{\mathrm{n}-1} \). In this manner, you will have created the points \( \mathrm{P}_{2}, \mathrm{P}_{3}, \ldots \ldots, \mathrm{P}_{\mathrm{n}} \ldots \ldots \), and joined them to create a beautiful spiral depicting
For the square root spiral follow the given steps:-
1. Draw a line \( A B \) of length 1 unit.
2. Draw another line \(BC\) of length 1 unit perpendicular to \(AB\).
3. Now, Join point \(A\) and point \(C\) forming a line \(AC\).
Here, \( A C \) represents a line of length \( \sqrt{2} \) units. (This can be easily found using Pythagoras Theorem in right \( \triangle A B C \) )
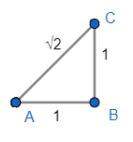
4. Now, Draw a perpendicular \( C D \) of length 1 unit at point \( C \) and join points \(A\) and \(D\). \(AD\) here represents length \( \sqrt{ } 3 \).
5. Similarly proceeding further we get Square Root Spiral.