Class 9 maths chapter 10 exercise 10.2 || exercise 10.2 class 9 solutions || class 9 exercise 10.2 || ncert solutions for class 9 chapter circles exercise 10.2 || exercise 10.2 class 9 || circles class 9 exercise 10.2 || class 9 circles exercise 10.2 || exercise 10.2 class 9 maths
Dive into clear, step-by-step solutions for Class 9 Maths Chapter 10, Exercise 10.2, which builds upon students’ understanding of the properties of circles by introducing theorems and their practical applications. This exercise guides learners through important concepts such as the perpendicular from the center to a chord, equal chords and their distances from the center, and the relationships between arcs and angles. Students use logical reasoning and geometric tools to explore how chords behave within a circle, applying previously learned principles about symmetry, congruence, and angles. Through visual analysis, structured proofs, and guided problem-solving, learners strengthen their ability to justify results and explain geometric relationships. Exercise 10.2 enhances critical thinking, proof-writing skills, and prepares students for advanced topics like geometry in the coordinate plane, constructions, and real-life problem-solving involving circular objects.

class 9 maths chapter 10 exercise 10.2 || exercise 10.2 class 9 solutions || class 9 exercise 10.2 || ncert solutions for class 9 chapter circles exercise 10.2 || exercise 10.2 class 9 || circles class 9 exercise 10.2 || class 9 circles exercise 10.2 || exercise 10.2 class 9 maths
Exercise 10.2
And thus, the shape of a circle depends on its radius. Therefore, it can be observed that if we try to superimpose two circles of equal radius, then both circles will cover each other

In \( \triangle \mathrm{AOB} \) and \( \Delta \mathrm{CO}^{\prime} \mathrm{D} \)
\( \mathrm{AB}=\mathrm{CD} \) (Chords of same length)
\( \mathrm{OA}=\mathrm{O}^{\prime} \mathrm{C} \) (Radii of congruent circles)
\( \mathrm{OB}=\mathrm{O}^{\prime} \mathrm{D} \) (Radii of congruent circles)
\( \Delta \mathrm{AOB} \cong \Delta \mathrm{CO}^{\prime} \mathrm{D} \) (SSS congruence rule)
\( \mathrm{AOB}=\mathrm{CO} \) 'D \( (\mathrm{By} \) CPCT\( ) \)
Hence, equal chords of congruent circles subtend equal angles at their centers.
class 9 maths chapter 10 exercise 10.2 || exercise 10.2 class 9 solutions || class 9 exercise 10.2 || ncert solutions for class 9 chapter circles exercise 10.2 || exercise 10.2 class 9 || circles class 9 exercise 10.2 || class 9 circles exercise 10.2 || exercise 10.2 class 9 maths
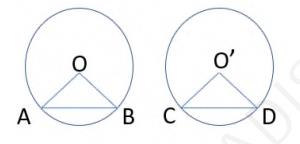
In \( \triangle \mathrm{AOB} \) and \( \Delta \mathrm{CO}^{\prime} \mathrm{D} \),
\( \mathrm{AOB}=\mathrm{CO}^{\prime} \mathrm{D} \) (Given)
\( \mathrm{OA}=\mathrm{O}^{\prime} \mathrm{C} \) (Radii of congruent circles)
\( \mathrm{OB}=\mathrm{O}^{\prime} \mathrm{D} \) (Radii of congruent circles)
\( \Delta \mathrm{AOB} \cong \Delta \mathrm{CO}^{\prime} \mathrm{D} \) (SAS congruence rule)
\( \mathrm{AB}=\mathrm{CD} \ (\text{By } \mathrm{CPCT}) \)
Hence, if chords of congruent circles subtend equal angles at their centers, then the chords are equal.

