Class 9 Maths Chapter 10 Exercise 10.4​

Let the radius of the circle centered at \( O \) and \( O^{\prime} \) be 5 cm and 3 cm respectively.
\({OA}={OB}=5 {~cm}\)
\({O}^{\prime} {A}={O}^{\prime} {B}=3 {~cm}\)
Also distance between their centers is 4 cm. So \( {OO}^{\prime}=4 {~cm} \)
The diagram is shown below:

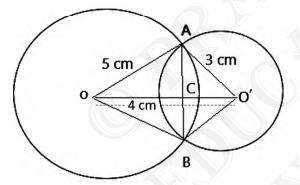
If two circles intersect each other at two points, then the line joining their centres is the perpendicular bisector of the common cord.
\(OO^{\prime} \) will be the perpendicular bisector of chord \(AB\)
\(\Rightarrow {AC}={CB}\)
Let \(OC\) be \(x \). Therefore, \( {O}^{\prime} {C} \) will be \( 4-{x} \)
In \( \triangle {OAC} \),
\({OA}^{2}={AC}^{2}+{OC}^{2}\)
\(\Rightarrow 5^{2}={AC}^{2}+{x}^{2}\)
\(\Rightarrow 25-{x}^{2}={AC}^{2}\quad \ldots\ldots\text{(i)}\)
Now, In \( \Delta {O}^{\prime} {AC} \),
\({O}^{\prime} {A}^{2}={AC}^{2}+{O}^{\prime} {C}^{2}\)
\(\Rightarrow 3^{2}={AC}^{2}+(4-{x})^{2}\)
\(\Rightarrow 9={AC}^{2}+16+{x}^{2}-8 {x}\)
\(\Rightarrow {AC}^{2}=-{x}^{2}-7+8 {x} \quad \ldots\ldots\text{(ii)}\)
From (i) and (ii), we get
\(25-x^{2}=-x^{2}-7+8 x\)
\(8 x=32\)
\(x=4\)
Hence, \( O^{\prime} C=4-4=0 {~cm} \) i.e. the common chord will pass through the centre of the smaller circle i.e., \( {O}^{\prime} \) and hence, it will be the diameter of the smaller circle.
Also, \( {AC}^{2}=25-{x}^{2} \)
\( =25-4^{2} \)
\( =25-16 \)
\( =9 \)
\( \Rightarrow {AC}=3 {~cm} \)
\( \Rightarrow \) Length of the common chord \( {AB}=2 {AC} \)
\( =(2 \times 3) {cm}=6 {~cm} \)

Let PQ and RS be two equal chords of a given circle and they are intersecting each other at point T
To prove: \( {PT}={RT} \)

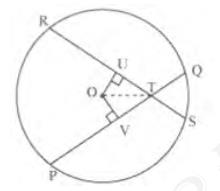
\({QT}={ST}\)
Draw perpendiculars OV and OU on these chords.
In \( \triangle {OVT} \) and \( \triangle {OUT} \),
\( {OV}={OU} \) (Equal chords of a circle are equidistant from the centre)
\( \angle {OVT}=\angle {OUT}\left(\text{Each } 90^{\circ}\right) \)
\( {OT}={OT} \) (Common)
\( \Delta {OVT} \cong \Delta {OUT} \) (RHS congruence rule)
\( {VT}={UT} \) (By CPCT) \(\quad \ldots\ldots\text{(i)}\)
It is given that,
\({PQ}={RS}\quad \ldots\ldots\text{(ii)}\)
\(\frac{1}{2} {PQ}=\frac{1}{2} {RS}\)
\({PV}={RU}\quad \ldots\ldots\text{(iii)}\)
On adding (i) and (iii), we get
\({PV}+{VT}={RU}+{UT}\)
\({PT}={RT}\quad \ldots\ldots\text{(iv)}\)
On subtracting equation (iv) from equation (ii), we obtain
\({PQ}-{PT}={RS}-{RT}\)
\({QT}={ST}\)
Therefore, \( {PT}={RT} \)
\( {QT}={ST} \) hence proved.

Let PQ and RS are two equal chords of a given circle and they are intersecting each other at point T

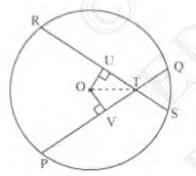
Draw perpendiculars OV and OU on these chords.
In \( \triangle {OVT} \) and \( \Delta {OUT} \),
\( {OV}={OU} \) (Equal chords of a circle are equidistant from the centre)
\( \angle {OVT}=\angle {OUT}\left(\text{Each } 90^{\circ}\right) \)
\( OT = OT\) (Common)
\( \Delta {OVT} \cong \Delta {OUT} \) (RHS congruence rule)
\( \angle {OTV}=\angle {OTU} \) (By congruent parts of congruent triangles)
Therefore, it is proved that the line joining the point of intersection to the centre makes equal angles with the chords.

Let us draw a perpendicular OM on line AD

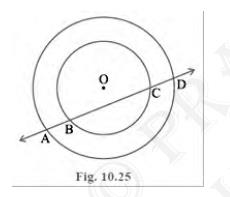
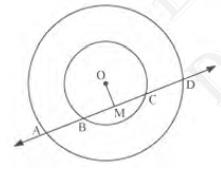
It can be observed that BC is the chord of the smaller circle and AD is the chord of the bigger circle
We know that perpendicular drawn from the centre of the circle bisects the chord
\({BM}={MC}\quad \ldots\ldots\text{(i)}\)
And \({AM}={MD}\quad \ldots\ldots\text{(ii)}\)
On subtracting (ii) from (i), we get
\({AM}-{BM}={MD}-{MC}\)
\({AB}={CD}\)
Hence proved

To Find: Distance between Reshma and Mandip
Given: Distance between Reshma and Salma and between Salma and Mandip is 6m
Diagram:

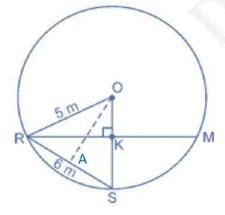
Explanation:
Draw perpendicular \(OA\) on \(RS\).
As \( OA \perp {RS} \),
\({RA}={AS}\)
Let \(R, S \) and \( M \) be the positions of Reshma, Salma and Mandip.
Now in \( \triangle {OAR} \) by Pythagoras theorem,
\({OR}^{2}={OA}^{2}+{RA}^{2}\)
\({OA}^{2}=5^{2}-3^{2}\)
\({OA}^{2}=25-9\)
\({OA}^{2}=16\)
\({OA}=4\)
Now we know,
Area of triangle \( =\frac{1}{2} \times {B} \times {H} \)
\(\text {Area }\Delta {ORS} =\frac{1}{2} \times {OS} \times {RK}\)
\(=\frac{1}{2} \times 5 \times {RK}\quad \ldots\ldots\text{(1)}\)
Also,
Area \( \triangle {ORS}=\frac{1}{2} \times {OA} \times {RS} \)
\(=\frac{1}{2} \times 4 \times 6\)
\(=12\quad \ldots\ldots\text{(2)}\)
From (1) and (2),
\(\frac{1}{2} \times 5 \times R K=12\)
\({RK}=\frac{12 \times 12}{5}\)
\({RK}=\frac{24}{5}\)
\({RK}=4.8 {~m}\)
As the perpendicular from the centre of a circle bisects the chord.
\(\text {As } {RM} =2 {RK}\)
\(= 2 \times 4.8\)
\(= 9.6 {~m}\)

The figure is shown as:

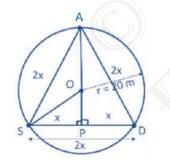
According to the given question,
\({AS}={AD}={SD}\)
Let \( {AS}={AD}={SD}=2 {x} \)
In \(ASD\), all sides are equal,
\( \therefore {ASD} \) is an equilateral triangle.
Now draw \( {OP} \perp {SD} \)
So, \( {SP}={DP}=\frac{1}{2} {SD} \)
\(\Rightarrow {SP}={DP}={x}\)
Join \(OS\) and \(AO\).
In \( \triangle OPS \),
\({OS}^{2}={OP}^{2}+{PS}^{2}\)
\((20)^{2}={OP}^{2}+{x}^{2}\)
\(400={OP}^{2}+{x}^{2}\)
In \( \triangle {APS} \),
\({AS}^{2}={AP}^{2}+{PS}^{2}\)
\((2 {x})^{2}={AP} ^{2}+{x} ^{2}\)
\(4 {x}^{2}={AP}^{2}+{x}^{2}\)
Now,
\(A P=A O+O P\)
\(\sqrt{3} x=20+\sqrt{400}-x^{2}\)
\(\sqrt{3} x-20=\sqrt{400}-x^{2}\)
Squaring both sides, we get,
\((\sqrt{3} x-20)^{2}=\left(\sqrt{400}-x^{2}\right)^{2}\)
\((\sqrt{3} x)^{2}+(20)^{2}-2 \times(\sqrt{3 x}) \times(20)=400-x^{2}\)
\(3 x^{2}+400-40 \sqrt{3} x=400-x^{2}\)
\(40 \sqrt{3} x=4 x^{2}\)
\(\frac{x^{2}}{x}=\frac{40 \sqrt{3}}{4}\)
\(x=10 \sqrt{3} m\)