Class 9 exercise 13.2 || class 9 surface area and volume exercise 13.2 || class 9 maths chapter 13 exercise 13.2 || ncert maths class 9 chapter 13 solutions || surface area and volume class 9 exercise13.2
Explore step-by-step solutions for Class 9 Maths Chapter 13, Exercise 13.2, which extends students’ understanding of Surface Areas and Volumes by focusing on the curved surface area, total surface area, and volume of a right circular cylinder. This exercise builds upon the foundational knowledge from earlier topics and introduces learners to more complex 3D shapes. By working through real-life word problems and practical applications, students enhance their ability to apply formulas accurately and understand the relationship between shape, space, and measurement. This not only sharpens their analytical thinking but also prepares them for deeper exploration of mensuration in higher mathematics.

class 9 exercise 13.2 || class 9 surface area and volume exercise 13.2 || class 9 maths chapter 13 exercise 13.2 || ncert maths class 9 chapter 13 solutions || surface area and volume class 9 exercise 13.2
Exercise 13.2
1. The curved surface area of a right circular cylinder of height
14 cm is \( 88 {~cm}^{2} \). Find the diameter of the base of the
cylinder.
Answer
Given: Height (h) of cylinder \( =14 {~cm} \), Curved surface area
of cylinder \( =88 {~cm}^{2} \)To Find: Diameter of the cylinder
Let the diameter of the cylinder be "d".
Formula used: Curved Surface Area of Cylinder \( =2 \pi {rh} \)
where, \( {r}= \) radius of the base of the cylinder and \( {h}= \) height of the cylinder \( 2 \pi {rh}=88 {~cm}^{2} \) (r is the radius of the base of the cylinder)
[Now, we know that 2 times radius \( = \) diameter, \( 2 {r}={d} \)]
\(\pi {dh}=88 {~cm}^{2}\)
\({d}=\frac{88 \times 7}{22 \times 14}\)
\(\frac{22}{7} \times {d} \times 14 {~cm}=88 {~cm}^{2}\)
\({d}=\frac{88 \times 7}{22 \times 14}\)
\({d}=2 {~cm}\)
Therefore, the diameter of the base of the cylinder is 2 cm
2. It is required to make a closed cylindrical tank of height 1 m
and base diameter 140 cm from a metal sheet. How many square
meters of the sheet are required for the same?
Answer
Height (h) of cylindrical tank \( =1 {~m} \) Base radius (r) of cylindrical tank
\(=70 {~cm}\)
\(=0.7 {~m}\)
Area of sheet required \( = \) Total surface area of tank
Area of sheet required \( =2 \pi {r}({r}+{h}) \)
Area of sheet required \( =2 \times \frac{22}{7} \times 0.7(0.7+1) \)
Area of sheet required \( =2 \times 22 \times 0.1 \times 1.7 \)
Area of Sheet Required \( =44 \times 0.17 \)
Area of sheet required \( =7.48 {~m}^{2} \)
class 9 exercise 13.2 || class 9 surface area and volume exercise 13.2 || class 9 maths chapter 13 exercise 13.2 || ncert maths class 9 chapter 13 solutions || surface area and volume class 9 exercise 13.2
3. A metal pipe is 77 cm long. The inner diameter of a cross
section is 4 cm, the outer diameter being 4.4 cm. Find its
(i) Inner curved surface area,
(ii) Outer curved surface area,
(iii) Total surface area
(i) Inner curved surface area,
(ii) Outer curved surface area,
(iii) Total surface area

Answer
\(\text {Radius }=\frac{\text { Diameter }}{2}\)Inner Radius \( \left(r_{1}\right)=\frac{4}{2}=2 {~cm} \)
Inner Radius \( \left(r_{1}\right)=\frac{4.4}{2}=2.2 {~cm} \)
Height \( = \) Length \( =77 {~cm} \)
Curved Surface Area of Cylinder \( =2 \pi {rh} \)
(i) C S A of inner surface of pipe \( =2 \pi r_{1} h \)
Inner surface Area of pipe \( =2 \times \frac{22}{7} \times 2 \times 77 \)
Inner surface Area of pipe \( =968 {~cm}^{2} \)
(ii) CSA of outer surface of pipe \( =2 \pi {r}^{2} {~h} \)
\(=2 \times \frac{22}{7} \times 2.2 \times 77\)
\(=2 \times 22 \times 2.2 \times 11\)
\(=1064.8 {~cm}^{2}\)
(iii) TSA \( = \) Inner CSA \(+\) Outer CSA \(+\) Area of both circular ends of pipe
\(=2 \pi {r}_{1} {~h}+2 \pi {r}_{2} {~h}+2 \pi\left({r}_{2}^{2}-{r}_{1}^{2}\right)\)
\(=\left[968+1064.8+2 \pi\left\{(2.2)^{2}-(2)^{2}\right\}\right] {cm}^{2}\)
\(=\left(2032.8+2 \times \frac{22}{7} \times 0.84\right) {cm}^{2}\)
\(=(2032.8+5.28) {cm}^{2}\)
\(=2038.08 {~cm}^{2}\)
Therefore, the total surface area of the cylindrical pipe is \( 2038.08 {~cm}^{2} \)
4. The diameter of a roller is 84 cm and its length is 120 cm. It
takes 500 complete revolutions to move once over to level a
playground. Find the area of the playground in \( {m}^{2} \).
Answer
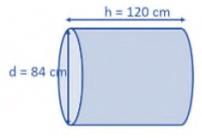
It can be observed that a roller is cylindrical
Height (h) of cylindrical roller \( = \) Length of roller
\( =120 {~cm} \)
Radius (r) of the circular end of roller \( =\frac{84}{2}=42 {~cm} \)
Curved Surface Area (CSA) of roller \( =2 \pi {rh} \)
\(=2 \times \frac{22}{7} \times 42 \times 120 {~cm}^{2}\)
\(=31680 {~cm}^{2}\)
Area of field \( =500 \times \) CSA of roller
\(=(500 \times 31680) {cm}^{2}\)
\(=15840000 {~cm}^{2}\)
\(=1584 {~m}^{2}\left(\because 1 {~m}^{2}=10000 {~cm}^{2}\right)\)
5. A cylindrical pillar is 50 cm in diameter and 3.5 m in height.
Find the cost of painting the curved surface of the pillar at the
rate of Rs 12.50 per \( {m}^{2} \)
Answer
Given:Height (h) cylindrical pillar \( =3.5 {~m} \)
Radius (r) of the circular end of pillar \( =\frac{50}{2}=25 {~cm}=0.25 {~m} \)
CSA of pillar \( =2 \pi {rh} \)
\(=2 \times \frac{22}{7} \times 0.25 \times 3.5 {~m}^{2}\)
\(=(44 \times 0.125) {m}^{2}\)
\(=5.5 {~m}^{2}\)
Cost of painting \( 1 {~m}^{2} \) area \( = \) Rs 12.50
Cost of painting \( 5.5 {~m}^{2} \) area \( =\operatorname{Rs}(5.5 \times 12.50) \)
\(=\text { Rs } 68.75\)
Therefore, the cost of painting the CSA of the pillar is Rs 68.75
6. Curved surface area of a right circular cylinder is \( 4.4
{~m}^{2} \). If the radius of the base of the cylinder is 0.7 m,
find its height
Answer
To Find: Height of the cylinderGiven: Curved surface area of cylinder \( =4.4 {~m}^{2} \) and radius of cylinder \( = \) 0.7 m
Concept Used:
Curved Surface Area of cylinder \( =2 \pi {rh} \)
where, \( r= \) radius of base of cylinder and \( h= \) height of cylinder
Explanation:
Let the height of the circular cylinder be \( h \)
\(2 \pi {rh}=4.4 {~m}^{2}\)
\((2 \times \frac{22 }{ 7} \times 0.7 \times {h}) {m} ^{2}=4.4 {~m}^{2}\)
\(4.4 {~h}=4.4 {~m}^{2}\)
\({h}=1 {~m}\)
Therefore, the height of the cylinder is 1 m .
class 9 exercise 13.2 || class 9 surface area and volume exercise 13.2 || class 9 maths chapter 13 exercise 13.2 || ncert maths class 9 chapter 13 solutions || surface area and volume class 9 exercise 13.2
7. The inner diameter of a circular well is 3.5 m. It is 10 m
deep.
Find
(i) Its inner curved surface area,
(ii) The cost of plastering this curved surface at the rate of Rs 40 per \( {m}^{2} \)
Find
(i) Its inner curved surface area,
(ii) The cost of plastering this curved surface at the rate of Rs 40 per \( {m}^{2} \)
Answer
Inner diameter of the circular well \( =3.5 {~m} \)Inner radius \( ({r}) \) of circular well \( =\frac{\text { Diameter }}{2} {~m} \)
\(=1.75 {~m}\)
Depth (h) of circular well \( =10 {~m} \)
(i) Inner curved surface area \( =2 \pi {rh} \)
\(=2 \times \frac{22}{7} \times 1.75 \times 10 {~m}^{2}\)
\(=(44 \times 0.25 \times 10) {m}^{2}\)
\(=110 {~m}^{2}\)
Therefore, the inner curved surface area of the circular well is \( 110 {~m}^{2} \).
(ii) Cost of plastering \( 1 {~m}^{2} \) area \( =\text{Rs } 40 \)
Cost of plastering \( 110 {~m}^{2} \) area \( =\text{Rs }(110 \times 40) \)
\(=\text {Rs } 4400\)
Therefore, the cost of plastering the CSA of this well is Rs 4400.
8. In a hot water heating system, there is a cylindrical pipe of
length 28 m and diameter 5 cm. Find the total radiating surface in
the system.
Answer
Height \( ({h}) \) of cylindrical pipe \( = \) Length of
cylindrical pipe \( =28 {~m} \)Radius (r) of circular end of pipe \( =\frac{5}{2} \)
\( =2.5 {~cm} \)
As \( 1 {~cm}=\frac{1}{100} {~m} \)
\( =0.025 {~m} \)
CSA of cylindrical pipe \( =2 \pi {rh} \)
\( =2 \times \frac{22}{7} \times 0.025 \times 28 {~m}^{2} \)
\(=4.4 {~m}^{2}\)
The area of the radiating surface of the system is \( 4.4 {~m}^{2} \)
9. Find
(i) The lateral or curved surface area of a closed cylindrical petrol storage tank that is 4.2 m in diameter and 4.5 m high.
(ii) How much steel was actually used, if \( \frac{1}{12} \) of the steel actually used was wasted in making the tank
(i) The lateral or curved surface area of a closed cylindrical petrol storage tank that is 4.2 m in diameter and 4.5 m high.
(ii) How much steel was actually used, if \( \frac{1}{12} \) of the steel actually used was wasted in making the tank
Answer
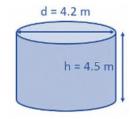
Height (h) of cylindrical tank \( =4.5 {~m} \)
\( \text{Radius (r)}=\left(\frac{4.2}{2}\right)=2.1 {~m} \)
(i) Lateral or curved surface area of tank \( =2 \pi {rh} \)
\(=2 \times \frac{22}{7} \times 2.1 \times 4.5\)
\(=(44 \times 0.3 \times 4.5) {m}^{2}\)
\(=59.4 {~m}^{2}\)
Therefore, the CSA of the tank is \( 59.4 {m}^{2} \).
(ii) Total surface area of \( \operatorname{tank}=2 \pi {r}({r}+{h}) \)
\(=2 \times \frac{22}{7} \times 2.1 \times(2.1+4.5) {m}^{2}\)
\(=(44 \times 0.3 \times 6.6) {m}^{2}\)
\(=87.12 {~m}^{2}\)
Let \( {x} {m}^{2} \) steel sheet be actually used in making the tank \( \frac{1}{12} \) of steel was wasted.
TSA \(=\) amount of steel \(-\) the amount of steel used
\( 87.12 {~m}^{2}={x}-\frac{1}{12} {x} \)
\({x}\left(1-\frac{1}{12}\right)=87.12 {~m}^{2}\)
\({x}=\left(\frac{12}{11} \times 87.12\right) {m}^{2}\)
\({x}=95.04 {~m}^{2}\)
Therefore, \( 95.04 {~m}^{2} \) steel was used in making such a tank.
10. In Fig. 13.12, you see the frame of a lampshade. It is to be
covered with a decorative cloth. The frame has a base diameter of
20 cm and height of 30 cm . A margin of 2.5 cm is to be given for
folding it over the top and bottom of the frame. Find how much
cloth is required for covering the lampshade.
Answer
Height (h) of the frame of lampshade \( =(2.5+30+2.5) {cm}=35
{~cm} \)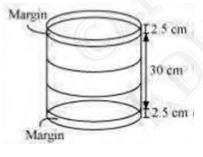
Radius (r) of the circular end of the frame of lampshade \( =\left(\frac{20}{2}\right) {cm}=10 \) cm
Cloth required for covering the lampshade \( = \) Curved Surface Area of the Cylinder \( =2 \pi {rh} \)
\(=2 \times \frac{22}{7} \times 10 \times 35 {~cm}^{2}\)
\(=2200 {~cm}^{2}\)
Hence, \( 2200 {~cm}^{2} \) cloth will be required for covering the lampshade.
11. The students of a Vidyalaya were asked to participate in a
competition for making and decorating penholders in the shape of a
cylinder with a base, using cardboard. Each penholder was to be of
radius 3 cm and height 10.5 cm. The Vidyalaya was to supply the
competitors with cardboard. If there were 35 competitors, how much
cardboard was required to be bought for the competition?
Answer
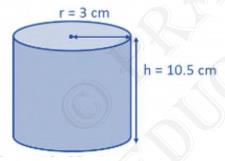
Radius (r) of the circular end of cylindrical pen holder \( =3 {~cm} \)
Height (h) of pen holder \( =10.5 {~cm} \)
for pen holder the curved Surface Area and Area of Base will be needed Surface area of 1 pen holder \( = \) CSA of pen holder \(+\) Area of base of pen holder
\(=2 \pi {rh}+\pi {r}^{2}\)
\(=\left[2 \times \frac{22}{7} \times 3 \times 10.5+\frac{22}{7} \times(3)^{2}\right] {cm}^{2}\)
\(=\left(132 \times 1.5+\frac{198}{7}\right) {cm}^{2}\)
\(=\left(198+\frac{198}{7}\right) {cm}^{2}\)
\(=\frac{(198 \times 7)+198}{7}\)
\(=\frac{1386+198}{7}\)
\(=\frac{1584}{7} {~cm}^{2}\)
Area of cardboard sheet used by 1 competitor \( =\frac{1584}{7} {~cm}^{2} \)
Area of cardboard sheet used by 35 competitors
\(=\frac{1584}{7} \times 35\)
\(=1584 \times 5\)
\(=7920 {~cm}^{2}\)

