Class 9 surface area and volume exercise 13.3 || class 9 maths chapter 13 exercise 13.3 || ncert maths class 9 chapter 13 solutions || class 9 exercise 13.3 || surface area and volume class 9 exercise 13.3
Explore step-by-step solutions for Class 9 Maths Chapter 13, Exercise 13.3, which deepens students’ understanding of Surface Areas and Volumes by focusing on the surface area and volume of a right circular cone. This exercise takes learners beyond the simpler shapes introduced earlier and challenges them to work with slant height, curved surface area, total surface area, and volume of conical structures. Through a variety of practical word problems and real-life scenarios, students learn how to apply standard formulas in a meaningful context. This strengthens their spatial reasoning, reinforces the connection between geometry and measurement, and equips them with essential skills for advanced topics in mensuration and real-world problem-solving.
class 9 surface area and volume exercise 13.3 || class 9 maths chapter 13 exercise 13.3 || ncert maths class 9 chapter 13 solutions || class 9 exercise 13.3 || surface area and volume class 9 exercise 13.3
Exercise 13.3
1. Diameter of the base of a cone is 10.5 cm and its slant height
is 10 cm. Find its curved surface area.
Answer
Radius (r) of the base of cone \( =\frac{10.5}{2} \)\(=5.25 {~cm}\)
Slant height (l) of cone \( =10 {~cm} \)
CSA of cone \( =\pi {rl} \)
\(=\frac{22}{7} \times 5.25 \times 10\)
\(=22 \times 0.75 \times 10\)
\(=165 {~cm}^{2}\)
Therefore, the curved surface area of the cone is \( 165 {~cm}^{2} \)
2. Find the total surface area of a cone, if its slant height is
21 m and diameter of its base is 24 m
Answer
Radius \( (r)=\frac{24}{2}=12 {~m} \)Slant height \( (l)=21 {~m} \)
TSA of cone \( =\pi {r}({r}+l) \)
\(=\frac{22}{7} \times 12(12+21)\)
\(=\frac{22}{7} \times 12 \times 33\)
\(=3.14 \times 396\)
\(=1243.44 {~m}^{2}\)
3. The curved surface area of a cone is \( 308 {~cm}^{2} \) and
its slant height is 14 cm. Find (i) radius of the base and (ii)
total surface area of the cone.
Answer
(i) Slant height (l) of cone \( =14 {~cm} \)Let the radius of the circular end of the cone be "\( r \)".
CSA of cone \( =\pi {rl} \)
\(308 {~cm}^{2}=\frac{22}{7} \times {r} \times 14\)
\({r}=\frac{308}{44}\)
\(=7 {~cm}\)
Therefore, the radius of the circular end of the cone is 7 cm .
(ii) The total surface area of cone \( = \) CSA of cone \(+\) Area of base
\(=\pi {rl}+\pi {r}^{2}\)
\(=\left[308+\frac{22}{7} \times(7)^{2}\right] {cm}^{2}\)
\(=(308+154) {cm}^{2}\)
\(=462 {~cm}^{2}\)
Therefore, the total surface area of the cone is \( 462 {~cm}^{2} \)
class 9 surface area and volume exercise 13.3 || class 9 maths chapter 13 exercise 13.3 || ncert maths class 9 chapter 13 solutions || class 9 exercise 13.3 || surface area and volume class 9 exercise 13.3
4. A conical tent is 10 m high and the radius of its base is 24
m. Find
(i) Slant height of the tent.
(ii) Cost of the canvas required to make the tent, if the cost of \( 1 {~m}^{2} \) canvas is Rs 70
(i) Slant height of the tent.
(ii) Cost of the canvas required to make the tent, if the cost of \( 1 {~m}^{2} \) canvas is Rs 70
Answer
(i) Let ABC be a conical tent.Height (h) of conical tent \( =10 {~m} \)
Radius (r) of conical tent \( =24 {~m} \)
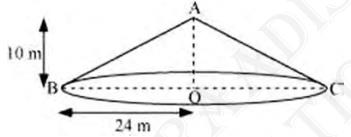
Let the slant height of the tent be 1.
In \( \triangle {ABO} \),
\({AB}^{2}={AO}^{2}+{BO}^{2}\)
\({l}^{2}={h}^{2}+{r}^{2}\)
\(=(10 {~m})^{2}+(24 {~m})^{2}\)
\(=676 {~m}^{2}\)
\({l}=26 {~m}\)
(ii) CSA of tent \( =\pi r l \)
\(=\frac{22}{7} \times 24 \times 26\)
\(=\frac{13728}{7} {~m}^{2}\)
Cost of \( 1 {~m}^{2} \) canvas \( = \) Rs 70
So, cost of \( \frac{13728}{7} {~m}^{2} \) canvas \( =\left(\frac{13728}{7} {~m}^{2} \times 70\right) \)
\(=\text { Rs } 137280\)
5. What length of tarpaulin 3 m wide will be required to make
conical tent of height 8 m and base radius 6 m ? Assume that the
extra length of material that will be required for stitching
margins and wastage in cutting is approximately 20 cm (Use \(
\pi=3.14 \))
Answer
To Find: Length of TarpaulinConcept Used:
Curved Surface Area of Cone \( =\pi {rl} \)
Diagram:
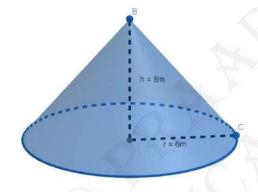
Height \( (h)=8 {~m} \)
Radius \(( r ) =6 {~m} \)
Now, we know that,
According to Pythagoras theorem, \( l^{2}={r} ^{2}+{h} ^{2} \)
\(\Rightarrow l^{2}=62+82\)
\(\Rightarrow l^{2}=(62+82)\)
\(\Rightarrow l^{2}=36+64\)
\(\Rightarrow l^{2}=100\)
\(\Rightarrow l=\sqrt{100 } =10 {~m}\)
Therefore, slant height of the conical tent \( =10 {~m} \).
CSA of conical tent \( =\pi {rl} \)
\(=\pi \times 6 {~m} \times 10 {~m}\)
\(=3.14 \times 6 {~m} \times 10 {~m}\)
\(=188.4 {~m}^{2}\)
Now, Let the length of tarpaulin sheet required be "\(x\)" m
As 20 cm will be wasted, therefore, the effective length will be \( =({x}-20 \) \( {cm})=({x}-0.2 {~m}) \)
Breadth of tarpaulin \( =3 {~m} \)
Area of sheet \( = \) CSA of tent
\(\Rightarrow[(x-0.2 {~m}) \times 3] {m}=188.4 {~m}^{2}\)
\(\Rightarrow {x}-0.2 {~m}=\frac{188.4}{3}\)
\(\Rightarrow {x}-0.2 {~m}=62.8 {~m}\)
\(\Rightarrow x=63 {~m}\)
Therefore, the length of the required tarpaulin sheet will be 63 m.
6. The slant height and base diameter of a conical tomb are 25 m
and 14 m respectively. Find the cost of white-washing its curved
surface at the rate of Rs 210 per \( 100 {~m}^{2} \)
Answer
Slant height (l) of conical tomb \( =25 {~m} \)Base radius (r) of tomb \( =\frac{14}{2} \)
\(=7 {~m}\)
CSA of conical tomb \( =\pi {rl} \)
\(=\frac{22}{7} \times 7 \times 25\)
\(=550 {~m}^{2}\)
Cost of white-washing \( 100 {~m}^{2} \) area \( = \) Rs 210
Cost of white-washing \( 550 {~m}^{2} \) area \( =\operatorname{Rs}\left(\frac{210 \times 550}{100}\right) \)
\( = \) Rs. 1155
Therefore, it will cost Rs 1155 while white-washing such a conical tomb.
7. A joker's cap is in the form of a right circular cone of base
radius 7 cm and height 24 cm. Find the area of the sheet required
to make 10 such caps.
Answer
Radius (r) \( =7 {~cm} \)Height (h) \( =24 {~cm} \)
Slant height \( ({l})=\sqrt{7 \times 7+24 \times 24} \)
\(=\sqrt{625}\)
\(=25 {~m}\)
\( \operatorname{CSA}(1 \) conical cap\( )=\pi r l \)
\(=\left(\frac{22}{7} \times 7 \times 25\right)\)
\(=550 {~cm}^{2}\)
CSA of 10 conical caps \( =(10 \times 550) \)
\(=5500 {~cm}^{2}\)
8. A bus stop is barricaded from the remaining part of the road,
by using 50 hollow cones made of recycled cardboard. Each cone has
a base diameter of 40 cm and height 1 m . If the outer side of
each of the cones is to be painted and the cost of painting is Rs
\( 12 {per}^{2} \), what will be the cost of painting all these
cones? (Use \( \pi=3.14 \) and take \( \sqrt{1.04} \) \( =1.02
\))
Answer
Radius (r) \( =\frac{40}{2}=20 {~cm} \)\(=0.2 {~m}\)
Height \( ({h})=1 {~m} \)
Slant height \( ({l})=\sqrt{1 \times 1+0.2 \times 0.2}\)
\(=\sqrt{1.04}\)
\(=1.02 {~m}\)
Curved Surface Area \( =\pi r l \)
\(=(3.14 \times 0.2 \times 1.02) {m}^{2}\)
\(=0.64056 {~m}^{2}\)
\(\operatorname{CSA}(50 \text { cones})=0.64056 \times 50 \)
\(=32.028 {~m}^{2}\)
Cost of painting \( 1 {~m}^{2} \) area \( = \) Rs 12
Cost of painting \( 32.028 {~m}^{2} \) area \( =\operatorname{Rs}(32.028 \times 12) \)
\( = \) Rs 384.336
\( = \) Rs 384.34 (approximately)
Therefore, it will cost Rs 384.34 in painting 50 such hollow cones.
