Ncert solutions for class 9 chapter Areas of Parallelograms and Triangles exercise 9.2 || Areas of Parallelograms and Triangles class 9 exercise 9.2 || exercise 9.2 class 9 || class 9 exercise 9.2 || class 9 Areas of Parallelograms and Triangles exercise 9.2 || exercise 9.2 class 9 solutions || class 9 maths chapter 9 exercise 9.2 || exercise 9.2 class 9 maths
Explore clear, step-by-step solutions for Class 9 Maths Chapter 9, Exercise 9.2, which introduces students to the fundamental concepts related to the areas of parallelograms and triangles. This exercise helps learners understand how geometric properties like base and height contribute to calculating area and how figures with the same base and height can have equal areas. By applying these concepts, students develop the ability to compare and analyze different shapes using mathematical reasoning. The problems are designed to reinforce visual understanding, logical interpretation and step-by-step proof-writing. Exercise 9.2 builds a strong foundation for advanced topics such as mensuration, coordinate geometry and practical applications of geometry in real life, encouraging both accuracy and conceptual clarity.

ncert solutions for class 9 chapter Areas of Parallelograms and Triangles exercise 9.2 || Areas of Parallelograms and Triangles class 9 exercise 9.2 || exercise 9.2 class 9 || class 9 exercise 9.2 || class 9 Areas of Parallelograms and Triangles exercise 9.2 || exercise 9.2 class 9 solutions || class 9 maths chapter 9 exercise 9.2 || exercise 9.2 class 9 maths
Exercise 9.2
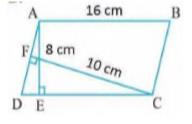
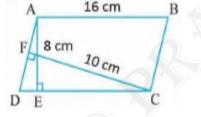
We know area of parallelogram \( = \) Base \( \times \) Height
For ABCD,
\( \mathrm{AE} \perp \mathrm{DC} \)
Hence AE is the height and DC is the base.
Area of \( \mathrm{ABCD}=\mathrm{DC} \times \mathrm{AE} \)
As we know sides of parallelogram are equal.
So, \( \mathrm{DC}=\mathrm{AB}=16 \mathrm{~cm} \)
Hence,
Area of \( \mathrm{ABCD}=16 \times 8 \ldots(1)\)
Also, for ABCD ,
\( \mathrm{CF} \perp \mathrm{AD} \)
Area of \( \mathrm{ABCD}=\mathrm{CF} \times \mathrm{AD} \)
\(=10 \times \mathrm{AD} \ldots(2)\)
From 1 and 2,
\(16 \times 8=10 \times \mathrm{AD}\)
\(\mathrm{AD}=\frac{16 \times 8}{10}\)
\(=12.8 \mathrm{~cm}\)
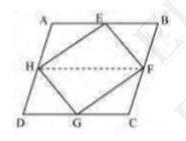
In parallelogram \( A B C D \),
\( \mathrm{AD}=\mathrm{BC} \) and \( \mathrm{AD} \| \mathrm{BC} \) (Opposite sides of a parallelogram are equal and parallel)
\( \mathrm{AB}=\mathrm{CD} \) (Opposite sides of a parallelogram are equal)
\(\frac{1}{2} \mathrm{AD}=\frac{1}{2} \mathrm{BC}\)
And \( \mathrm{AH} \| \mathrm{BF} \)
\( \mathrm{AH}=\mathrm{BF} \) and \( \mathrm{AH} \| \mathrm{BF}(\mathrm{H} \) and F are the mid-points of AD and BC )
Therefore, ABFH is a parallelogram
Since,
\( \triangle \mathrm{HEF} \) and parallelogram ABFH are on the same base HF and between the same parallel lines AB and HF
Therefore,
Area of triangle \( \mathrm{HEF}=\frac{1}{2} \times \) Area \( (\mathrm{ABFH})\ldots(i)\)
Similarly,
It can also be proved that
Area of triangle \( \mathrm{HGF}=\frac{1}{2} \times \) Area \((HDCF) \ldots(ii)\)
On adding (i) and (ii), we get
Area of triangle \( \mathrm{HEF}+ \) Area of triangle \( \mathrm{HGF}=\frac{1}{2} \mathrm{Area}(\mathrm{ABFH})+\frac{1}{2} \) Area (HDCF)
\( \operatorname{Area}(\mathrm{EFGH})=\frac{1}{2}[\operatorname{Area}(\mathrm{ABFH})+\operatorname{Area}(\mathrm{HDCF})] \)
\( \operatorname{Area}(\mathrm{EFGH})=\frac{1}{2} \operatorname{Area}(\mathrm{ABCD}) \)
ncert solutions for class 9 chapter Areas of Parallelograms and Triangles exercise 9.2 || Areas of Parallelograms and Triangles class 9 exercise 9.2 || exercise 9.2 class 9 || class 9 exercise 9.2 || class 9 Areas of Parallelograms and Triangles exercise 9.2 || exercise 9.2 class 9 solutions || class 9 maths chapter 9 exercise 9.2 || exercise 9.2 class 9 maths
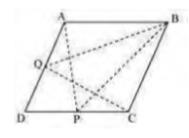
If a triangle and parallelogram are on the same base and have the same altitude,
the area of the triangle will be half that of the parallelogram.
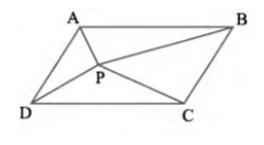
Area \( (\triangle \mathrm{BQC})=\operatorname{Area}(\mathrm{ABCD})\ldots(i)\)
Similarly,
If a triangle and parallelogram are on the same base and have the same altitude,
the area of the triangle will be half that of the parallelogram.
\( \triangle \mathrm{APB} \) and parallelogram ABCD lie on the same base AB
and between the same parallel lines AB and DC
\( \operatorname{Area}(\triangle \mathrm{APB})=\frac{1}{2} \operatorname{Area}(\mathrm{ABCD}) \ldots(ii)\)
From equation (i) and (ii), we get
\( \operatorname{Area}(\triangle \mathrm{BQC})=\operatorname{Area}(\triangle \mathrm{APB}) \)
(i) \( \operatorname{ar}(\mathrm{APB})+\operatorname{ar}(\mathrm{PCD})=\frac{1}{2} \operatorname{ar}(\mathrm{ABCD}) \)
(ii) \( \operatorname{ar}(\mathrm{APD})+\operatorname{ar}(\mathrm{PBC})=\operatorname{ar}(\mathrm{APB})+\operatorname{ar}(\mathrm{PCD}) \)
[Hint: Through P, draw a line parallel to AB ]
(i) Let us draw a line segment EF, passing through point P and parallel to line segment AB .
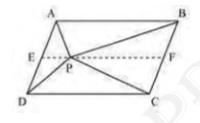
In parallelogram \( A B C D \)
\( \mathrm{AB} \| \mathrm{EF} \) (By construction) \(\ldots(i)\)
\( \mathrm{AD} \| \mathrm{BC} \) (Opposite sides of a parallelogram)
So, \( \mathrm{AE} \| \mathrm{BF}\ldots(ii)\)
From equations (i) and (ii), we get
Quadrilateral ABFE is a parallelogram.
It can be observed that \( \triangle \mathrm{APB} \) and parallelogram ABFE are lying on the same base \( A B \) and between the same parallel lines \( A B \) and \( E F \)
Therefore,
Area of triangle \( \mathrm{APB}=\frac{1}{2} \times \) Area \( (\mathrm{ABFE}) \ldots(iii) \)
Similarly, we show that EFCD is a parallelogram,
For triangle PCD and parallelogram EFCD, lying on same base CD and same parallel lines,
Area of triangle PCD \( =\frac{1}{2} \times \) Area (EFCD) \( \ldots(iv)\)
Adding (iii) and (iv), we get
Area of triangle APB + Area of triangle \( \mathrm{PCD}=\frac{1}{2}[ \) Area \( (\mathrm{ABFE})+ \) Area (EFCD) \( ] \)
Area of triangle APB + Area of triangle \( \mathrm{PCD}=\frac{1}{2} \) Area (ABCD) \( \ldots (v)\)
(ii) Let us draw a line segment MN, passing through point P and parallel to line segment AD
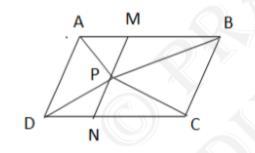
In parallelogram \( A B C D \),
\( \mathrm{MN} \| \mathrm{AD} \) (By construction) \(\ldots(vi)\)
ABCD is a parallelogram
\( \mathrm{AB} \| \mathrm{DC} \) (Opposite sides of a parallelogram)
So, \( A M \| D N \ldots(vii)\)
From equations (vi) and (vii), we get
\( \mathrm{MN} \| \mathrm{AD} \) and
AM ||DN
Therefore,
Quadrilateral AMND is a parallelogram.
It can be observed that \( \triangle \mathrm{APD} \) and parallelogram AMND are lying on the same base \( A D \) and between the same parallel lines \( A D \) and \( M N \)
\( \operatorname{Area}(\triangle \mathrm{APD})=\frac{1}{2} \) Area \( (\mathrm{AMND}) \ldots(viii)\)
Similarly,
For \( \triangle \mathrm{PCB} \) and parallelogram MNCB ,
\( \operatorname{Area}(\triangle \mathrm{PCB})=\frac{1}{2} \operatorname{Area}(\mathrm{MNCB})\ldots(ix)\)
Adding equations (viii) and (ix), we get
\( \operatorname{Area}(\triangle \mathrm{APD})+\operatorname{Area}(\triangle \mathrm{PCB})=\frac{1}{2}[\operatorname{Area}(\mathrm{AMND})+\operatorname{Area}(\mathrm{MNCB})] \)
\( \operatorname{Area}(\triangle \mathrm{APD})+\operatorname{Area}(\triangle \mathrm{PCB})=\frac{1}{2} \operatorname{Area}(\mathrm{ABCD})\ldots(x)\)
On comparing equations (v) and (x), we get
\( \operatorname{Area}(\triangle \mathrm{APD})+\operatorname{Area}(\triangle \mathrm{PBC})=\operatorname{Area}(\triangle \mathrm{APB})+\operatorname{Area}(\Delta \mathrm{PCD}) \)
(i) \( \operatorname{\text {ar}}(\mathrm{PQRS})= \) ar \( (\mathrm{ABRS}) \)
(ii) \( \operatorname{ar}(\mathrm{AXS})=\frac{1}{2} \operatorname{ar}(\mathrm{PQRS}) \)
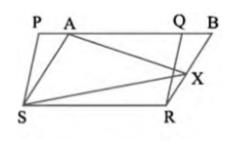
Area \( ( \) PQRS \( )=\operatorname{Area}( ABRS )\ldots(i) \)
(ii) Consider \( \triangle \mathrm{AXS} \) and parallelogram ABRS
As these lie on the same base AS and are between the same parallel lines AS and BR,
\( \operatorname{ar}(\mathrm{AXS})=\frac{1}{2} \operatorname{ar}( ABRS ) \ldots(ii)\)
From equations (i) and (ii), we obtain
\( \operatorname{ar}(\mathrm{AXS})=\frac{1}{2} \operatorname{ar}(\mathrm{PQRS}) \)
Hence proved.
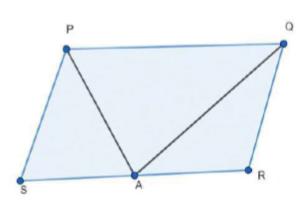
Area of \( \triangle \mathrm{PSA}+ \) Area of \( \triangle \mathrm{PAQ}+ \) Area of \( \triangle \mathrm{QRA}= \) Area of Parallelogram \(PQRS \ldots(i)\)
We know that if a parallelogram and a triangle are on the same base and between the same parallels, then the area of the triangle is half the area of the parallelogram
Therefore,
\( \operatorname{Area}(\triangle \mathrm{PAQ})=\frac{1}{2} \operatorname{Area}(\mathrm{PQRS}) \ldots(ii)\)
From equations (i) and (ii), we obtain
\( \operatorname{Area}(\triangle \mathrm{PSA})+\operatorname{Area}(\triangle \mathrm{QRA})+\frac{1}{2} \operatorname{Area}(\mathrm{PQRS})=\operatorname{Area}(\mathrm{PQRS}) \)
\( \operatorname{Area}(\triangle \mathrm{PSA})+\operatorname{Area}(\triangle \mathrm{QRA})=\frac{1}{2} \operatorname{Area}(\mathrm{PQRS}) \ldots(iii)\)
Clearly, it can be observed that the farmer must sow wheat in triangular part \(PAQ\)
and pulses in other two triangular parts \(PSA\) and \(QRA\) or wheat in triangular parts \(PSA\) and \(QRA\) and pulses in triangular parts \(PAQ\).

