Exercise 9.4 class 9 || class 9 exercise 9.4 || class 9 Areas of Parallelograms and Triangles exercise 9.4 || Areas of Parallelograms and Triangles class 9 exercise 9.4 || class 9 maths chapter 9 exercise 9.4 || exercise 9.4 class 9 maths || exercise 9.4 class 9 solutions || ncert solutions for class 9 chapter Areas of Parallelograms and Triangles exercise 9.4
Explore clear, step-by-step solutions for Class 9 Maths Chapter 9, Exercise 9.4, which helps students apply and extend their understanding of the area properties of triangles and parallelograms in more advanced geometric contexts. This exercise focuses on using previously learned concepts—such as figures having the same base and lying between the same parallels—to solve complex problems and justify conclusions through logical reasoning and structured proofs. It challenges students to analyze different geometric configurations and make accurate comparisons of area. Exercise 9.4 strengthens skills in visualization, proof-writing, and mathematical explanation, while also preparing learners for more advanced studies in mensuration, coordinate geometry, and real-life applications of geometry.

exercise 9.4 class 9 || class 9 exercise 9.4 || class 9 Areas of Parallelograms and Triangles exercise 9.4 || Areas of Parallelograms and Triangles class 9 exercise 9.4 || class 9 maths chapter 9 exercise 9.4 || exercise 9.4 class 9 maths || exercise 9.4 class 9 solutions || ncert solutions for class 9 chapter Areas of Parallelograms and Triangles exercise 9.4
Exercise 9.4
Consider the parallelogram ABCD and rectangle ABEF as follows
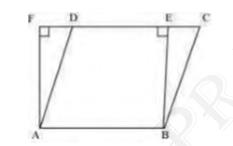
Here, it can be observed that parallelogram ABCD and rectangle ABEF are between the same parallels AB and CF
We know that opposite sides of a parallelogram or a rectangle are of equal lengths
Therefore,
\( \mathrm{AB}=\mathrm{EF} \) (For rectangle)
\( \mathrm{AB}=\mathrm{CD} \) (For parallelogram)
\( \mathrm{CD}=\mathrm{EF} \)
\( \mathrm{AB}+\mathrm{CD}=\mathrm{AB}+\mathrm{EF} \ldots(i)\)
Of all the line segments that can be drawn to a given line from a point not lying on it, the perpendicular line segment is the shortest
\(\mathrm{AF} < \mathrm{AD} \)
And similarly,
\( \mathrm{BE} < \mathrm{BC} \)
\( \mathrm{AF}+\mathrm{BE} < \mathrm{AD}+\mathrm{BC} \ldots(ii)\)
From equations (i) and (ii), we obtain
\(\mathrm{AB}+\mathrm{EF}+\mathrm{AF}+\mathrm{BE} < \mathrm{AD}+\mathrm{BC}+\mathrm{AB}+\mathrm{CD}\)
Perimeter of rectangle \( A B E F < \) Perimeter of parallelogram \( A B C D \)
Can you now answer the question that you have left in the 'Introduction' of this chapter, whether the field of Budhia has been actually divided into three parts of equal area?

[Remark: Note that by taking \( \mathrm{BD}=\mathrm{DE}=\mathrm{EC} \), the triangle ABC is divided into three triangles \( \mathrm{ABD}, \mathrm{ADE} \) and AEC of equal areas. In the same way, by dividing BC into unequal parts and joining the points of division so obtained to the opposite vertex of \( B C \), you can divide \( \triangle \mathrm{ABC} \) into n triangles of equal areas]

We know that,
Area of a triangle \( =\frac{1}{2} * \) Base \( * \) Altitude
\( \operatorname{Area}(\triangle \mathrm{ADE})=\frac{1}{2} * \mathrm{DE}^{*} \mathrm{AM} \)
\( \operatorname{Area}(\triangle \mathrm{ABD})=\frac{1}{2} * \mathrm{BD} * \mathrm{AM} \)
\( \operatorname{Area}(\triangle \mathrm{AEC})=\frac{1}{2} * \mathrm{EC} * \mathrm{AM} \)
It is given that \( \mathrm{DE}=\mathrm{BD}=\mathrm{EC} \)
\( \frac{1}{2} \times \mathrm{DE} \times \mathrm{AM}=\frac{1}{2} \times \mathrm{BD} \times \mathrm{AM}=\frac{1}{2} \times \mathrm{EC} \times \mathrm{AM} \)
\( \operatorname{Area}(\triangle \mathrm{ADE})=\operatorname{Area}(\triangle \mathrm{ABD})=\operatorname{Area}(\triangle \mathrm{AEC}) \)
It can be observed that Budhia has divided her field into 3 equal parts
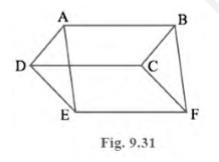
\(\mathrm{AD}=\mathrm{BC}\ldots(i)\)
Similarly, for parallelograms DCEF and ABFE
\(\mathrm{DE}=\mathrm{CF}\ldots(ii)\)
And,
\(\mathrm{EA}=\mathrm{FB} \ldots(iii)\)
In \( \triangle \mathrm{ADE} \) and \( \triangle \mathrm{BCF} \),
\( \mathrm{AD}=\mathrm{BC} \quad[ \) Using equation (i)]
\( \mathrm{DE}=\mathrm{CF} \quad[ \) Using equation (ii)]
\( \mathrm{EA}=\mathrm{FB} \quad[ \) Using equation (iii)]
\( \triangle \mathrm{ADE} \cong \mathrm{BCF} \) (SSS congruence rule)
\( \operatorname{Area}(\triangle \mathrm{ADE})=\operatorname{Area}(\triangle \mathrm{BCF}) \)
exercise 9.4 class 9 || class 9 exercise 9.4 || class 9 Areas of Parallelograms and Triangles exercise 9.4 || Areas of Parallelograms and Triangles class 9 exercise 9.4 || class 9 maths chapter 9 exercise 9.4 || exercise 9.4 class 9 maths || exercise 9.4 class 9 solutions || ncert solutions for class 9 chapter Areas of Parallelograms and Triangles exercise 9.4
[Hint: Join AC]
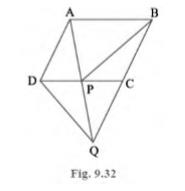
\( \mathrm{AD} \| \mathrm{BC} \) and \( \mathrm{AB} \| \mathrm{DC} \) (Opposite sides of a parallelogram are parallel to each other)
Join point \( A \) to point \( C \)
Consider \( \triangle \mathrm{APC} \) and \( \triangle \mathrm{BPC} \)
\( \triangle \mathrm{APC} \) and \( \triangle \mathrm{BPC} \) are lying on the same base PC and between the same parallels \( P C \) and \( A B \)
Therefore,
\( \operatorname{Area}(\triangle \mathrm{APC})=\operatorname{Area}(\triangle \mathrm{BPC})\ldots(i)\)
In quadrilateral \( A C D Q \)
\(\mathrm{AD}=\mathrm{CQ}\)
Since,
ABCD is a parallelogram
\( \mathrm{AD} \| \mathrm{BC} \) (Opposite sides of a parallelogram are parallel)
\( C Q \) is a line segment which is obtained when line segment \( B C \) is produced
\( \mathrm{AD} \| \mathrm{CQ} \)
We have,
\( \mathrm{AC}=\mathrm{DQ} \) and \( \mathrm{AC} \| \mathrm{DQ} \)
Hence, \( A C Q D \) is a parallelogram
Consider \( \triangle \mathrm{DCQ} \) and \( \triangle \mathrm{ACQ} \)
These are on the same base CQ and between the same parallels \( C Q \) and AD
Therefore,
\( \operatorname{Area}(\triangle \mathrm{DCQ})=\operatorname{Area}(\triangle \mathrm{ACQ}) \)
\( \operatorname{Area}(\triangle \mathrm{DCQ})-\operatorname{Area}(\triangle \mathrm{PQC})=\operatorname{Area}(\triangle \mathrm{ACQ})-\operatorname{Area}(\triangle \mathrm{PQC}) \)
\( \operatorname{Area}(\triangle \mathrm{DPQ})=\operatorname{Area}(\triangle \mathrm{APC})\ldots(ii)\)
From equations (i) and (ii), we obtain
\( \operatorname{Area}(\triangle \mathrm{BPC})=\operatorname{Area}(\Delta \mathrm{DPQ}) \)
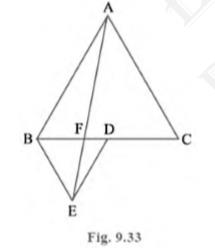
(i) \( \operatorname{ar}(\mathrm{BDE})=\frac{1}{4} \operatorname{ar}(\mathrm{ABC}) \)
(ii) \( \operatorname{ar}(\mathrm{BDE})=\frac{1}{2} \operatorname{ar}(\mathrm{BAE}) \)
(iii) \( \operatorname{ar}(\mathrm{BFE})=\operatorname{ar}(\mathrm{AFD}) \)
(iv) ar \( (\mathrm{ABC})=2 \) ar \( (\mathrm{BEC})\)
(v) ar \( (\mathrm{BFE})=2 \) ar \( (\mathrm{FED}) \)
(vi) \( \operatorname{ar}( FED )=\frac{1}{8} \operatorname{ar}(\mathrm{AFC}) \)
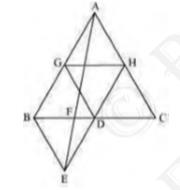
\( \mathrm{GH}=\frac{1}{2} \mathrm{BC} \) and
\( \mathrm{GH} \| \mathrm{BD} \)
\( \mathrm{GH}=\mathrm{BD}=\mathrm{DC} \) and \( \mathrm{GH} \| \mathrm{BD} \) ( D is the mid-point of BC )
Consider quadrilateral GHDB
\( \mathrm{GH} \| \mathrm{BD} \) and \( \mathrm{GH}=\mathrm{BD} \)
Two line segments joining two parallel line segments of equal length will also be equal and parallel to each other
Therefore,
\( \mathrm{BG}=\mathrm{DH} \) and \( \mathrm{BG} \| \mathrm{DH} \)
Hence, quadrilateral GHDB is a parallelogram
We know that in a parallelogram, the diagonal bisects it into two triangles of equal area
Hence,
\( \operatorname{Area}(\Delta \mathrm{BDG})=\operatorname{Area}(\Delta \mathrm{HGD}) \)
Similarly, it can be proved that quadrilaterals DCHG, GDHA, and BEDG are parallelograms and their respective diagonals are dividing them into two triangles of equal area
\( \operatorname{ar}(\Delta \mathrm{GDH})=\operatorname{ar}(\Delta \mathrm{CHD})( \) For parallelogram DCHG) ar \( (\triangle \mathrm{GDH})=\operatorname{ar} \) \( (\triangle \mathrm{HAG}) \) (For parallelogram GDHA) ar \( (\triangle \mathrm{BDE})=\operatorname{ar}(\triangle \mathrm{DBG})( \) For parallelogram BEDG)
\( \operatorname{ar}(\Delta \mathrm{ABC})=\operatorname{ar}(\Delta \mathrm{BDG})+\operatorname{ar}(\Delta \mathrm{GDH})+\operatorname{ar}(\Delta \mathrm{DCH})+\operatorname{ar}(\Delta \mathrm{AGH}) \)
\( \operatorname{ar}(\Delta \mathrm{ABC})=4 \times \operatorname{ar}(\Delta \mathrm{BDE}) \)
Hence,
\( \operatorname{ar}(\triangle \mathrm{BDE})=\frac{1}{2} \operatorname{ar}(\mathrm{ABC}) \)
(ii)Area \( (\triangle \mathrm{BDE})=\operatorname{Area}(\triangle \mathrm{AED})( \) Common base DE and \( \mathrm{DE} \| \mathrm{AB}) \)
\( \operatorname{Area}(\triangle \mathrm{BDE})-\operatorname{Area}(\triangle \mathrm{FED})=\operatorname{Area}(\Delta \mathrm{AED})-\operatorname{Area}(\Delta \mathrm{FED}) \)
\( \operatorname{Area}(\triangle \mathrm{BEF})=\operatorname{Area}(\triangle \mathrm{AFD})\ldots(i)\)
\( \operatorname{Area}(\triangle \mathrm{ABD})=\operatorname{Area}(\triangle \mathrm{ABF})+\operatorname{Area}(\triangle \mathrm{AFD}) \)
\( \operatorname{Area}(\triangle \mathrm{ABD})=\operatorname{Area}(\triangle \mathrm{ABF})+\operatorname{Area}(\triangle \mathrm{BEF})[ \) From equation (i) \( ] \)
\( \operatorname{Area}(\triangle \mathrm{ABD})=\operatorname{Area}(\triangle \mathrm{ABE})\ldots(ii)\)
AD is the median in \( \triangle \mathrm{ABC} \)
\( \operatorname{Area}(\triangle \mathrm{ABD})=\frac{1}{2} \operatorname{Area}(\triangle \mathrm{ABC}) \)
\( = \) Area \( (\triangle \mathrm{BDE}) \)
\( \operatorname{Area}(\triangle \mathrm{ABD})=2 \) Area \( (\triangle \mathrm{BDE}) \ldots(iii)\)
From (ii) and (iii), we obtain
2 ar \( (\triangle \mathrm{BDE})=\operatorname{ar}(\triangle \mathrm{ABE}) \)
\( \operatorname{ar}(\triangle \mathrm{BDE})=\operatorname{ar}(\triangle \mathrm{ABE}) \)
(iii) ar \( (\triangle \mathrm{ABE})= \) ar \( (\triangle \mathrm{BEC})( \) Common base BE and \( \mathrm{BE} \| \mathrm{AC}) \)
\( \operatorname{ar}(\triangle \mathrm{ABF})+\operatorname{ar}(\triangle \mathrm{BEF})=\operatorname{ar}(\triangle \mathrm{BEC}) \)
Using equation (i), we obtain
\begin{array}{l}
\operatorname{ar}(\triangle \mathrm{ABF})+\operatorname{ar}(\triangle \mathrm{AFD})=\operatorname{ar}(\triangle \mathrm{BEC}) \operatorname{ar}(\triangle \mathrm{ABD})=\operatorname{ar}(\triangle \mathrm{BEC}) \\
\operatorname{ar}(\triangle \mathrm{ABC})=\operatorname{ar}(\triangle \mathrm{BEC}) \\
\operatorname{ar}(\triangle \mathrm{ABC})=2 \operatorname{ar}(\triangle \mathrm{BEC})
\end{array}
(iv) It is seen that \( \triangle \mathrm{BDE} \) and ar \( \triangle \mathrm{AED} \) lie on the same base (DE) and between the parallels \( D E \) and \( A B \)
\( \operatorname{ar}(\triangle \mathrm{BDE})=\operatorname{ar}(\triangle \mathrm{AED}) \operatorname{ar}(\triangle \mathrm{BDE})-\operatorname{ar}(\triangle \mathrm{FED}) \)
\( =\operatorname{ar}(\triangle \mathrm{AED})-\operatorname{ar}(\triangle \mathrm{FED}) \operatorname{ar}(\Delta \mathrm{BFE})=\operatorname{ar}(\triangle \mathrm{AFD}) \)
(v)
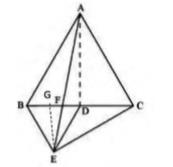
An in equilateral triangle, median drawn is also perpendicular to the side,
\( \therefore A D \perp B C \)
Now,
ar \( \Delta \mathrm{AFD}=\frac{ 1 }{ 2 } \times \mathrm{FD} \times \mathrm{AD} \ldots(i)\)
Draw EG \( \perp \) BC.
Draw EGBC
ar \( \Delta \mathrm{FED}=\frac{ 1 }{ 2 } \times \mathrm{FD} \times \mathrm{EG} \ldots(ii)\)
Dividing eq. (i) by (ii), we get
\(\frac{a r \triangle A F D}{\operatorname{ar} \triangle F E D}=\frac{\frac{1}{2} \times F D \times A D}{\frac{1}{2} \times F D \times E G}\)
As Altitude of equilateral triangle \( = \) side
\(\frac{\operatorname{ar} \triangle A F D}{\operatorname{ar} \triangle F E D}=\frac{\frac{\sqrt{3}}{4} B C}{\frac{\sqrt{3}}{4} B D}=\frac{B C}{B D}\)
As \( D \) is the mid-point of \( B C \).
\(\frac{a r \triangle A F D}{a r \triangle F E D}=\frac{2 B D}{B D}\)
\(\frac{a r \triangle A F D}{a r \triangle F E D}=2\)
\( \operatorname{ar}(\triangle \mathrm{AFD})=2 \) ar \( (\triangle \mathrm{FED}) \ldots(iii)\)
From part (iii) ar \( (\mathrm{BFE})= \) ar \( (\mathrm{AFD}) \)
So ar \( (\triangle \mathrm{BFE})=2 \) ar \( (\triangle \mathrm{FED}) \)
(vi) \(\text{ar} (\Delta \mathrm{AFC})=\operatorname{ar}(\Delta \mathrm{AFD})+\operatorname{ar}(\Delta \mathrm{ADC})=2 \operatorname{ar}(\Delta \mathrm{FED})+\operatorname{ar}(\Delta ABC)\) [using (v)]
\( =2 \operatorname{ar}(\Delta \mathrm{FED})+\frac{1}{2}[4 \times \operatorname{ar}(\Delta \mathrm{BDE})]\quad \) [Using result of part (i)]
\( =2 \operatorname{ar}(\Delta \mathrm{FED})+2 \operatorname{ar}(\Delta \mathrm{BDE})=2 \operatorname{ar}(\Delta \mathrm{FED})+2 \operatorname{ar}(\Delta \mathrm{AED}) \)
[ \( \triangle \mathrm{BDE} \) and \( \triangle \mathrm{AED} \) are on the same base and between same parallels]
\(=2 \operatorname{ar}(\Delta \mathrm{FED})+2[\operatorname{ar}(\triangle \mathrm{AFD})+\operatorname{ar}(\Delta \mathrm{FED})]\)
\(=2 \operatorname{ar}(\Delta \mathrm{FED})+2 \operatorname{ar}(\triangle \mathrm{FFD})+2 \operatorname{ar}(\Delta \mathrm{FED})[\text { Using (viii) }]\)
\(=4 \operatorname{ar}(\Delta \mathrm{FED})+4 \operatorname{ar}(\Delta \mathrm{FED})\)
\(\Rightarrow \operatorname{ar}(\Delta \mathrm{FFC})=8 \operatorname{ar}(\Delta \mathrm{FED})\)
\(\Rightarrow \operatorname{ar}(\Delta \mathrm{FED})=\frac{1}{8}[\operatorname{ar}(\triangle \mathrm{AFC})]\)
exercise 9.4 class 9 || class 9 exercise 9.4 || class 9 Areas of Parallelograms and Triangles exercise 9.4 || Areas of Parallelograms and Triangles class 9 exercise 9.4 || class 9 maths chapter 9 exercise 9.4 || exercise 9.4 class 9 maths || exercise 9.4 class 9 solutions || ncert solutions for class 9 chapter Areas of Parallelograms and Triangles exercise 9.4
Download the Math Ninja App Now[Hint: From A and C, draw perpendiculars to BD]
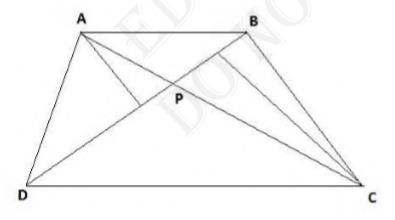
Let us construct AM perpendicular to BD
Now,
\(\text { Area (APB) x Area (CPD) }\)
\({\left[\frac{1}{2} \times B P \times A M\right] \times\left[\frac{1}{2} P D \times C N\right]}\)
\(=\frac{1}{4} \times B P \times A M \times P D \times C N\)
Hence,
Area \( (\mathrm{APB}) \times \) Area \( (\mathrm{CPD})= \) Area \( (\mathrm{APD}) \times \) Area \( (\mathrm{CPB}) \)
(i) \( \operatorname{ar}(\mathrm{PRQ})=\frac{1}{2} \operatorname{ar}(\mathrm{ARC}) \)
(ii) \( \operatorname{ar}(\mathrm{RQC})=\frac{3}{8} \operatorname{ar}(\mathrm{ABC}) \)
(iii) \( \operatorname{ar}(\mathrm{PBQ})=\operatorname{ar}(\mathrm{ARC}) \)
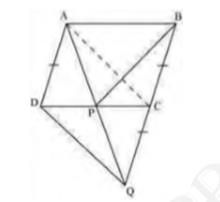
Let ABC is a triangle.
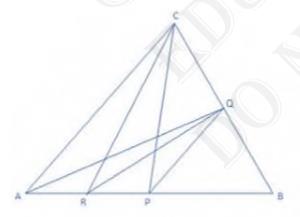
P and Q are the midpoints of AB and BC respectively and R is the midpoint of AP.
Join PQ, QR, AQ, PC, RC as shown in the figure.
Now we know that the median of a triangle divides it into two triangles of equal areas.
In triangle CAP, CR is the median.
So \( \operatorname{Area}(\Delta \mathrm{CRA})=\left(\frac{1}{2}\right) \times \operatorname{Area}(\triangle \mathrm{CAP}) \ldots(1)\)
Again in triangle \( \mathrm{CAB}, \mathrm{CP} \) is the median.
\( \operatorname{So} \operatorname{Area}(\Delta \mathrm{CAP})=\left(\frac{1}{2}\right) \times \operatorname{Area}(\Delta \mathrm{CPB}) \ldots(2)\)
from equation 1 and 2 , we get
\( \operatorname{Area}(\triangle \mathrm{CAP})=\left(\frac{1}{2}\right) \times \operatorname{Area}(\triangle \mathrm{CPB}) \ldots(3)\)
Again in triangle \( \mathrm{PBC}, \mathrm{PQ} \) is the median.
\( \operatorname{So}\left(\frac{1}{2}\right) \times \operatorname{Area}(\Delta \mathrm{CPB})=\operatorname{Area}(\Delta \mathrm{PBQ}) \ldots(4)\)
From equation 3 and 4 , we get
\( \operatorname{Area}(\triangle \mathrm{ARC})=\operatorname{Area}(\Delta \mathrm{PBQ}) \ldots(5)\)
Now QP, And QR are the medians of triangle QAB and QAP respectively
So \( \operatorname{Area}(\Delta \mathrm{QAP})=\operatorname{Area}(\Delta \mathrm{QBP}) \ldots(6)\)
and \( \operatorname{Area}(\Delta \mathrm{QAP})=2 \times \operatorname{Area}(\Delta \mathrm{QRP}) \ldots(7)\)
from equation 6 and 7 , we get
\( \operatorname{Area}(\Delta \mathrm{PRQ})=\left(\frac{1}{2}\right) \times \operatorname{Area}(\Delta \mathrm{PBQ}) \ldots(8)\)
from equation 5 and 8 , we get
\( \operatorname{Area}(\Delta \mathrm{PRQ})=\left(\frac{1}{2}\right) \times \operatorname{Area}(\Delta \mathrm{ARC}) \)
Now CR is the median of triangle CAP
\(\text { So Area }(\Delta \mathrm{ARC})=\left(\frac{1}{2}\right) \times \operatorname{Area}(\Delta \mathrm{CAP})\)
\(=\left(\frac{1}{2}\right) \times\left(\frac{1}{2}\right) \times \operatorname{Area}(\Delta \mathrm{ABC})\)
\(=\left(\frac{1}{4}\right) \times \operatorname{Area}(\Delta \mathrm{ABC})\)
Again RQ is the median of triangle RBC
\(\text { So Area } (\Delta \mathrm{RQC})=\left(\frac{1}{2}\right) \times \operatorname{Area}(\Delta \mathrm{RBC})\)
\( =\left(\frac{1}{2}\right) \times \operatorname{Area}(\Delta \mathrm{ABC})-\left(\frac{1}{2}\right) \times \operatorname{Area}(\Delta \mathrm{ARC})\)
\( =\left(\frac{1}{2}\right) \times \operatorname{Area}(\Delta \mathrm{ABC})-\left(\frac{1}{2}\right) \times\left(\frac{1}{2}\right) \times\left(\frac{1}{2}\right) \times \operatorname{Area}(\Delta \mathrm{ABC})\)
\( =\left(\frac{1}{2}\right) \times \operatorname{Area}(\Delta \mathrm{ABC})-\left(\frac{1}{8}\right) \times \operatorname{Area}(\Delta \mathrm{ABC})\)
\( =\left(\frac{3}{8}\right) \times \operatorname{Area}(\Delta \mathrm{ABC})\)
So \( \operatorname{Area}(\Delta \mathrm{RQC})=\left(\frac{3}{8}\right) \times \operatorname{Area}(\Delta \mathrm{ABC}) \)
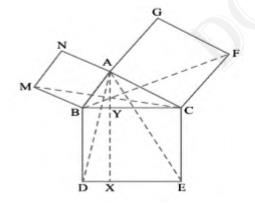
(i) \( \Delta \mathrm{MBC} \cong \Delta \mathrm{ABD} \)
(ii) ar \( (\mathrm{BYXD})=2 \) ar \( (\mathrm{MBC}) \)
(iii) ar \( (B Y X D)= \) ar \( (A B M N) \)
(iv) \( \Delta \mathrm{FCB} \cong \Delta \mathrm{ACE} \)
(v) \( \operatorname{ar}(\mathrm{CYXE})=2 \) ar \((FCB)\)
(vi) ar \( (\mathrm{CYXE})= \) ar \( (\mathrm{ACFG}) \)
(vii) ar \( (\mathrm{BCED})= \) ar \( (\mathrm{ABMN})+\operatorname{ar}(\mathrm{ACFG}) \)
Note: Result (vii) is the famous Theorem of Pythagoras. You shall learn a simpler proof of this theorem in Class \(X\).
Hence, angle \( \mathrm{ABM}= \) angle \( \mathrm{DBC}=90^{\circ} \)
\(\begin{array}{l}
\mathrm{ABM}+\mathrm{ABC}=\mathrm{DBC}+\mathrm{ABC} \\
\mathrm{MBC}=\mathrm{ABD}\ldots(1)
\end{array}\)
In \( \triangle \mathrm{MBC} \) and \( \triangle \mathrm{ABD} \),
Angle MBC = Angle ABD (From 1)
\( \mathrm{MB}=\mathrm{AB} \) (Sides of square)
\( B C=B D( \) Sides of square)
Therefore,
By SAS congruence rule,
(ii) Now, we have:
And we know that adjacent sides of square are perpendicular to each other. Hence,
BD perpendicular DE
And,
\(AX\) perpendicular DE
Also,
We know that two lines perpendicular to the same line are parallel to each other.
Therefore,
\( \mathrm{BD} \| \mathrm{AX} \)
Now,
Area \( \triangle A B D=\left(\frac{1}{2}\right) \) Area \( ( B X Y D)(\triangle A B D \) and \( \| g m \ BXYD\) are on same base \( B D \) and betweeen the same parallels \( B C \) and \( A X \mid \)
Area \( (B X Y D)=2 \) area \( (\triangle \mathrm{ABD}) \)
Area \( (\mathrm{BXYD})=2 \) area \( (\triangle \mathrm{MBC})\ldots(2) \)
(iii) \( \triangle \mathrm{MBC} \) and parallelogram ABMN are on same base MB and between the same parallels MB and NC.
Therefore,
\( \operatorname{Area}(\triangle \mathrm{MBC})= \frac{1}{2} \) ar \( (\mathrm{ABMN}) \)
\( 2 \operatorname{Area}(\triangle M B C)=\operatorname{Area}(A B M N)=\operatorname{Area}(B X Y D)( \) From 2) \(\ldots(3)\)
(iv) Since, each angle of square is \( 90^{\circ} \)
Therefore,
Angle FCA \( = \) Angle \( \mathrm{BCE}=90^{\circ} \)
\( \mathrm{FCA}+\mathrm{ACB}=\mathrm{BCE}+\mathrm{ACB} \)
Angle FCB = Angle ACE
Now,
In \( \triangle \mathrm{FCB} \) and \( \triangle \mathrm{ACE} \),
Angle FCB = Angle ACE
\( \mathrm{FC}=\mathrm{AC} \) (Sides of square)
\( \mathrm{CB}=\mathrm{CE}( \) Sides of square \( ) \)
Therefore,
By SAS congruence,
\(\triangle M B C \cong \triangle A B D\)
(v) It is given that \(AX\) is perpendicular to \(DE\) and \(CE\) is perpendicular to \(DE\) and,
We know that two lines perpendicular to the same line are parallel to each other.
Hence,
\( \mathrm{CE} \| \mathrm{AX} \)
Now,
\( \triangle \mathrm{ACE} \) and parallelogram \(CYXE\) are on same base \(CE\) and between the same parallels \(CE\) and \(AX \).
Therefore,
\( \operatorname{Area}(\triangle \mathrm{ACE})=\frac{1}{2} \operatorname{Area}(\mathrm{CYXE}) \)
Area \( (\mathrm{CYXE})=2 \operatorname{Area}(\triangle \mathrm{ACE})\ldots(4)\)
We had proved that
\( \Delta \mathrm{FCB} \ \Delta \mathrm{ACE} \)
Hence,
\( \operatorname{Area}(\triangle \mathrm{ACE})=\operatorname{Area}(\Delta \mathrm{FCB})\ldots(5)\)
Comparing 4 and 5 , we get:
\( \mathrm{CYXE}=2 \operatorname{Area}(\Delta \mathrm{FCB})\ldots(6)\)
(vi) \( \triangle \mathrm{FCB} \) and parallelogram ACFG are on same base CF and between the same parallels CF and BG
Hence,
Area \( (\triangle \mathrm{FCB})= \frac{1}{2}\) Area \( (\mathrm{ACFG}) \)
Area \( (\mathrm{ACFG})=2 \) Area \( (\triangle \mathrm{FCB})=\operatorname{Area}(\mathrm{CYXE})( \) Using 6\( )(7) \)
(vii) From figure:
Area \( (B C E D)=\operatorname{Area}(B X Y D)+\operatorname{Area}( CYXE ) \)
Area \( (\mathrm{BCED})=\operatorname{Area}(\mathrm{ABMN})+\operatorname{Area}(\mathrm{ACFG})( \) using 3 and 7 )

