Exercise 12.1 class 9 || ncert maths class 9 chapter 12 solutions || class 9 maths herons formula exercise 12.1 || class 9 maths chapter 12 exercise 12.1 || class 9 maths exercise 12.1 solution || class 9 exercise 12.1 || class 9 maths statistics exercise 12.1 || class 9 math exercise 12.1
Explore step-by-step solutions for Class 9 Maths Chapter 12, Exercise 12.1, which introduces students to Heron’s Formula—a powerful tool for finding the area of a triangle when all three sides are known. This exercise builds on earlier geometry lessons and challenges learners to apply the formula in a variety of contexts, including real-life word problems. By engaging with these problems, students develop a deeper understanding of how algebra and geometry work together. The exercise enhances logical thinking, sharpens analytical skills, and lays the groundwork for solving complex geometrical problems in higher classes with confidence and accuracy.

exercise 12.1 class 9 || ncert maths class 9 chapter 12 solutions || class 9 maths herons formula exercise 12.1 || class 9 maths chapter 12 exercise 12.1 || class 9 maths exercise 12.1 solution || class 9 exercise 12.1 || class 9 maths statistics exercise 12.1 || class 9 math exercise 12.1
Exercise 12.1
1. A traffic signal board, indicating 'SCHOOL AHEAD', is an
equilateral triangle with side '\( a \)'. Find the area of the
signal board, using Heron's formula. If its perimeter is 180 cm,
what will be the area of the signal board?
Answer
Given
Perimeter of Signal board \( =180 \mathrm{~cm} \)
Length of the side of the equilateral triangle \( =\mathrm{a} \)
The perimeter of the signal board \( = \) perimeter of the triangle
(Perimeter of Equilateral Triangle \( =3 \times \) Side \( ) \)
\(3 \mathrm{a}=180 \mathrm{~cm}\)
\(\mathrm{a}=60 \mathrm{~cm}\)
Therefore, each side of triangle \( =60 \mathrm{~cm} \).
Semi perimeter of the signal board \( (\mathrm{s})= \) \(\frac{ \text{Perimeter of board} }{ 2 }\)
\(=\frac{ 180 }{ 2 }= \) 90 cm
Using Heron's formula,
Area of the signal board \( =\sqrt{s(s-a)(s-b)(s-c)} \)
where, \( \mathrm{s}= \) semi perimeter of signal board \( =90 \mathrm{~cm} \mathrm{~a}=\mathrm{b}=\mathrm{c}=60 \mathrm{~cm} \)
Putting the value we
Area of signal board \( =\sqrt{90(90-60)(90-60)(90-60)} \)
Area of signal board \( =\sqrt{90 \times 30 \times 30 \times 30} \)
Area of signal board \( =100 \times 9 \sqrt{3} \)
Area of signal board \( =900 \sqrt{3} \mathrm{~cm}^{2} \)
Method 2:
we know that,
Area of an equilateral triangle \( =\frac{\sqrt{3}}{4} a^{2} \)
where \( \mathrm{a}= \) side of the equilateral triangle. putting the value of \( \mathrm{a}=60 \mathrm{~cm} \) we get,
Area \( =\frac{\sqrt{3}}{4}(60)^{2} \)
Area \( =\frac{\sqrt{3}}{4} \times 3600 \)
Area \( =900 \sqrt{3} \mathrm{~cm}^{2} \)
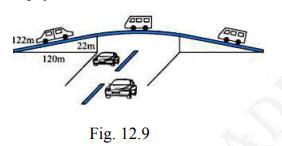
2. The triangular side walls of a flyover have been used for
advertisements. The sides of the walls are \( 122 \mathrm{~m}, 22
\mathrm{~m} \) and 120 m (see Fig. 12.9). The advertisements yield
on earning of Rs 5000 per \(\mathrm{m}^{2} \) per year. A company
hired one of its walls for 3 months. How much rent did it pay?

Answer
As shown in the figure the sides of the triangular side walls of
flyover are \( 122 \mathrm{~m}, 22 \mathrm{~m} \), and 120 m .Perimeter of the triangle \( =122+22+120=264 \mathrm{~m} \)
Semi perimeter of triangle(s) \( =\frac{264}{2} \)
\(=132 \mathrm{~m}\)
Now,
Using Heron's formula
Area of the advertisement \( =\sqrt{s(s-a)(s-b)(s-c)} \)
where, \( s= \) semi perimeter of triangle and \( a, b \), and \( c \) are the sides of the triangle.
\(=\sqrt{132(132-122)(132-22)(132-120)}\)
\(=\sqrt{132 \times 10 \times 110 \times 12}\)
\(=\sqrt{132 \times 132 \times 10 \times 10}\)
\(=132 \times 10 \mathrm{~m}^{2}\)
\( =1320 \mathrm{~m}^{2} \)
Rent of advertising per year \( = \) Rs. 5000 per \( \mathrm{m}^{2} \)
Rent of one wall for 1 year \( =1320 \times 5000 \)
Rent of one wall for 3 months \( =\frac{1320 \times 5000 \times 3}{12} \)
Rent of one wall for 3 months \( = \) Rs. 1650000
exercise 12.1 class 9 || ncert maths class 9 chapter 12 solutions || class 9 maths herons formula exercise 12.1 || class 9 maths chapter 12 exercise 12.1 || class 9 maths exercise 12.1 solution || class 9 exercise 12.1 || class 9 maths statistics exercise 12.1 || class 9 math exercise 12.1
3. There is a slide in a park. One of its side walls has been
painted in some color with a message "KEEP THE PARK GREEN AND
CLEAN" (see Fig. 12.10). If the sides of the wall are \( 15
\mathrm{~m}, 11 \mathrm{~m} \) and 6 m , find the area painted in
color.


Answer
Given: The sides of the triangle are \( 15 \mathrm{~m}, 11
\mathrm{~m} \) and 6 m .To find: Area painted in color
Explanation:
Perimeter of the triangular walls \( = \) sum of 3 sides
Perimeter \( =15+11+6=32 \mathrm{~m} \)
Semi perimeter of triangular walls \( (\mathrm{s})=\frac{32}{2} \)
\(=16 \mathrm{~m}\)
Using Heron's formula,
Area of the advertisement \( = \) Area of triangle
\( =\sqrt{s(s-a)(s-b)(s-c)} \)
where, \( \mathrm{s}= \) semi perimeter of the triangle \( \mathrm{a}, \mathrm{b} \) and c are the sides of the triangle Therefore for the given triangle,
\(\text {Area }=\sqrt{16(16-15)(16-11)(16-6)}\)
\(=\sqrt{16 \times 1 \times 5 \times 10}\)
\(=\sqrt{16 \times 5 \times 10}\)
\(=\sqrt{800} \mathrm{~m}^{2}\)
\( =\sqrt{(20 \times 20 \times 2}) \) (Taking 20 outside the square root, as a pair is present in square root, we get,)
\(=20 \sqrt{2} \mathrm{~m}^{2}\)
Thus the area of painted color is \( 20 \sqrt{2} \mathrm{~m}^{2} \)
4. Find the area of a triangle two sides of which are 18 cm and
10 cm and the perimeter is 42 cm .
Answer
To find: Area of the triangleGiven:
Two sides of the triangle are 18 cm and 10 cm (Given)
Perimeter of the triangle \( =42 \mathrm{~cm} \)
Perimeter of Triangle \( = \) Sum of sides of triangle
Let the third side of triangle be \( x \), So
\(x+18+10=42\)
Third side of triangle, \( x=42-(18+10) \)
\(=14 \mathrm{~cm}\)
Semi perimeter of triangle \( (\mathrm{s})=\frac{42}{2} \)
\(=21 \mathrm{~cm}\)
Using Heron's formula,
\(\text { Area of the triangle }=\sqrt{s(s-a)(s-b)(s-c)}\)
\(=\sqrt{21(21-18)(21-10)(21-14)}\)
\(=\sqrt{21 \times 3 \times 11 \times 7}\)
\(=\sqrt{7 \times 3 \times 7 \times 3 \times 11}\)
\(=21 \sqrt{11} \mathrm{~cm}^{2}\)
5. Sides of a triangle are in the ratio of \(12: 17: 25\) and its
perimeter is 540 cm . Find its area.
Answer
Let the common ratio of the sides of the triangle be \(x\) and
sides are \( 12 x, 17 x\) and \(25 x\)The perimeter of the triangle \( =540 \mathrm{~cm} \)
Sum of sides of the triangle \( =540 \mathrm{~cm} \)
\(12 x+17 x+25 x=540 \mathrm{~cm}\)
\(54 x=540\)
\(x=10\)
Sides of triangle:
\(12 x=12 \times 10=120 \mathrm{~cm}\)
\(17 x=17 \times 10=170 \mathrm{~cm}\)
\(25 x=25 \times 10=250 \mathrm{~cm}\)
Semi perimeter of triangle \( (\mathrm{s})=\frac{540}{2} \)
\(=270 \mathrm{~cm}\)
Now,
Using Heron's formula,
Area of the triangle \( =\sqrt{s(s-a)(s-b)(s-c)} \)
where, \( \mathrm{s}= \) semi-perimeter of the triangle and \( \mathrm{a}, \mathrm{b} \) and c are the sides of the triangle
\(=\sqrt{270(270-120)(270-170)(270-250)}\)
\(=\sqrt{270 \times 150 \times 100 \times 20}\)
\(=\sqrt{ (81000000)} \mathrm{cm}^{2}\)
\(=9000 \mathrm{~cm}^{2}\)
Area of triangle \( =9000 \mathrm{~c m}^{2} \)
6. An isosceles triangle has perimeter 30 cm and each of the
equal sides is 12 cm. Find the area of the triangle.
Answer
Length of equal sides of the triangle \( =12 \mathrm{~cm} \)Perimeter of the triangle \( =30 \mathrm{~cm} \)
Third side of triangle \( =30-(12+12) \)
\(=6 \mathrm{~cm}\)
Semi perimeter of triangle \( (\mathrm{s})=\frac{30}{2} \)
\( =15 \mathrm{~cm} \)
Now,
Using Heron's formula,
Area of the triangle \( =\sqrt{s(s-a)(s-b)(s-c)} \)
where, \( s= \) semi perimeter of the triangle
\( \mathrm{a}, \mathrm{b} \) and c are the sides of the triangle
\(=\sqrt{15(15-12)(15-12)(15-6)}\)
\(=\sqrt{15 \times 3 \times 3 \times 9}\)
\(=9 \sqrt{15} \mathrm{~cm}^{2}\)
Hence, the area of triangle is \( 9 \sqrt{15} \mathrm{~cm}^{2} \)

