Heron's formula class 9 exercise 12.2 || ncert maths class 9 chapter 12 solutions || class 9 maths heron's formula exercise 12.2 || class 9 maths chapter 12 exercise 12.2 || class 9 exercise 12.2 || class 9 math exercise 12.2 || exercise 12.2 class 9 || class 9 maths exercise 12.2 solution
Explore step-by-step solutions for Class 9 Maths Chapter 12, Exercise 12.2, which introduces students to Heron’s Formula—a powerful tool for finding the area of a triangle when all three sides are known. This exercise builds on earlier geometry lessons and challenges learners to apply the formula in a variety of contexts, including real-life word problems. By engaging with these problems, students develop a deeper understanding of how algebra and geometry work together. The exercise enhances logical thinking, sharpens analytical skills and lays the groundwork for solving complex geometrical problems in higher classes with confidence and accuracy.

heron's formula class 9 exercise 12.2 || ncert maths class 9 chapter 12 solutions || class 9 maths heron's formula exercise 12.2 || class 9 maths chapter 12 exercise 12.2 || class 9 exercise 12.2 || class 9 math exercise 12.2 || exercise 12.2 class 9 || class 9 maths exercise 12.2 solution
Exercise 12.2
1. A park, in the shape of a quadrilateral ABCD , has \( \angle
\mathrm{C}=90^{\circ} \), \( \mathrm{AB}=9 \mathrm{~m},
\mathrm{BC}=12 \mathrm{~m}, \mathrm{CD}=5 \mathrm{~m} \) and \(
\mathrm{AD}=8 \mathrm{~m} \). How much area does it occupy?
Answer
The figure is given below: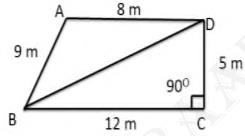
The dimensions of the park as follows:
Angle \( \mathrm{C}=90^{\circ} \),
\(\mathrm{AB}=9 \mathrm{~m}\)
\(\mathrm{BC}=12 \mathrm{~m}\)
\(\mathrm{CD}=5 \mathrm{~m}\)
And, \( \mathrm{AD}=8 \mathrm{~m} \)
Now, BD is joined.
Thus quadrilateral ABCD can now be divided into two triangles ABD and BCD
Area of quadrilateral \( \mathrm{ABCD}= \) Area of triangle \( \mathrm{ABD}+ \) Area of triangle BCD
Pythagoras Theorem: It states that the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides.
In \( \triangle \mathrm{BCD} \) by Pythagoras theorem,
\(\mathrm{BD}^{2}=\mathrm{BC}^{2}+\mathrm{CD}^{2}\)
\(\mathrm{BD}^{2}=122+5^{2}\)
\(\mathrm{BD}^{2}=169\)
\(\mathrm{BD}=13 \mathrm{~m}\)
As triangle BCD is right angled triangle,
Area of \( \triangle B C D=\frac{1}{2} \times \) base \( \times \) height
Area of \( \triangle B C D=\frac{1}{2} \times 12 \times 5=30 \mathrm{~m}^{2} \)
Now, Semi perimeter of triangle \( (\mathrm{ABD})=\frac{(8+9+13)}{2} \)
\(=\frac{30}{2}=15 \mathrm{~m}\)
Using Heron's formula,
\(\operatorname{ar}(\mathrm{ABD})=\sqrt{s(s-a)(s-b)(s-c)}\)
where, \( \mathrm{s}= \) semi-perimeter of the triangle and \( \mathrm{a}, \mathrm{b} \), and c are the sides of the triangle.
\(=\sqrt{15(15-13)(15-8)(15-9)}\)
\(=\sqrt{15 \times 2 \times 7 \times 6}\)
\(=\sqrt{6 \times 6 \times 5 \times 7}\)
\(=6 \sqrt{35 }\mathrm{m}^{2}\)

\(=6 \times 5.91=35.46 \mathrm{~m}^{2}\)
Area of quadrilateral \( \mathrm{ABCD}=35.46+30 \)
Area of quadrilateral \( \mathrm{ABCD}=65.46 \mathrm{~m}^{2} \)
Thus, the park acquires an area of \( 65.5 \mathrm{~m}^{2} \) (approx).
2. Find the area of a quadrilateral \( A B C D \) in which \( A
B=3 \mathrm{~cm} \), \( \mathrm{BC}=4 \mathrm{~cm}, \mathrm{CD}=4
\mathrm{~cm}, \mathrm{DA}=5 \mathrm{~cm} \) and \( \mathrm{AC}=5
\mathrm{~cm} \).
Answer
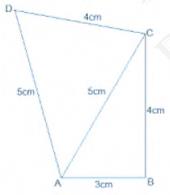
Given: \( \mathrm{AB}=3 \mathrm{~cm}, \mathrm{BC}=4 \mathrm{~cm}, \mathrm{CD}=4 \mathrm{~cm}, \mathrm{DA}=5 \mathrm{~cm} \) and \( \mathrm{AC}=5 \mathrm{~cm} \)
To find: Area of quadrilateral ABCD.
Now we can divide the quadrilateral into two separate triangles and then calculate their area. Now, in \( \triangle \mathrm{ABC} \),
Using Pythagoras theorem,
\(\mathrm{AC}^{2}=\mathrm{BC}^{2}+\mathrm{AB}^{2}\)
\(5^{2}=3^{2}+4^{2}\)
\(25=16+9\)
\(25=25\)
Thus,
Triangle \( \triangle A B C \) is right angled triangle and since AB and BC are smaller sides so they work as legs.
And we know that,
Area of right angles triangle \( =\frac{1}{2} \times \) base \( \times \) height
\(\operatorname{ar}(\mathrm{ABC})=\frac{1}{2} \times 3 \times 4=6 \mathrm{~cm}^{2}\)
Now,
Perimeter of \( =5+5+4 \)
Semi perimeter of \( \triangle \mathrm{ACD}=\frac{5+5+4}{2} \)
\(=\frac{14}{2}\)
\(=7 \mathrm{~cm}\)
Using Heron's formula,
Area of \( \triangle \mathrm{ACD}=\sqrt{s(s-a)(s-b)(s-c)} \)
where, \( s= \) semi perimeter of the triangle and \( a, b \), and \( c \) are the sides of the triangle
\(=\sqrt{7(7-5)(7-5)(7-4)}\)
\(=\sqrt{2 \times 2 \times 7 \times 3}\)
\(=2 \sqrt{21} \mathrm{~cm}^{2}\)
Take \( =\sqrt{21}=4.58 \)
\(=9.16 \mathrm{~cm}^{2} \text { (approx) }\)
Area of quadrilateral \( \mathrm{ABCD}= \) Area of \( \triangle A B C+ \) Area of \( \triangle \mathrm{ACD} \)
\(=6+9.16\)
\(=15.16 \mathrm{~cm}^{2}\)
By rounding off \( =15.2 \mathrm{~cm}^{2} \) (approx)
3. Radha made a picture of an aero plane with colored paper as
shown in Fig 12.15. Find the total area of the paper used.
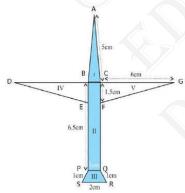

Answer
The figure of the questions is: 
Now to find area:
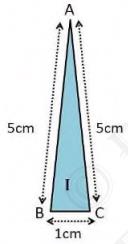
Sides of triangular section \( \mathrm{I}=5 \mathrm{~cm}, 1 \mathrm{~cm} \) and 5 cm
Perimeter of the triangular section \( \mathrm{I}=5+5+1=11 \mathrm{~cm} \)
Semi perimeter,
\( \mathrm{s}=\frac{\text { perimeter of triangular section } I}{2}=\frac{11}{2}=5.5 \mathrm{~cm} \)
We use Heron's formula to find the area of the section I,
Area of Section \( \mathrm{I}=\sqrt{s(s-a)(s-b)(s-c)} \)
\(=\sqrt{5.5(5.5-5)(5.5-5)(5.5-1)}\)
\(=\sqrt{5.5 \times 0.5 \times 0.5 \times 4.5}\)
\(=\sqrt{6.1875} \mathrm{~cm}^{2}\)
Area of Section \( \mathrm{I}=2.48 \mathrm{~cm}^{2} \) (approx.) \( \sim 2.5 \mathrm{~cm}^{2} \)
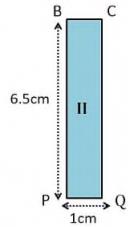
Length of the sides of the rectangle of section \(\mathrm{II}=6.5 \mathrm{~cm} \) and 1 cm Area of section \( \mathrm{II}=6.5 \times 1=6.5 \mathrm{~cm}^{2} \)
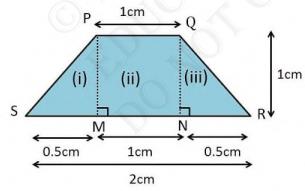
Section III is an isosceles trapezium which is divided into two right triangles and one rectangle.
Now, Area of trapezium
\(=\text { Area (i) }+ \text { Area (ii) + Area (iii) }\)
\(=\frac{ 1 }{ 2 } \times 0.5 \times 1+1 \times 1+\frac{ 1 }{ 2 } \times 0.5 \times 1=1.5 \mathrm{~cm}^{2}\)
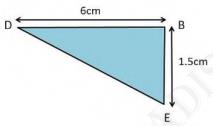
Section IV and V are congruent right-angled triangles with height 1.5 cm and base 6 cm .
now area of triangle,
\(=\frac{1}{2} \times \text { base } \times \text { height }=\frac{1}{2} \times 1.5 \times 6\)
\(=4.5 \mathrm{~cm}^{2}\)
Area of region IV and \( \mathrm{V}=2 \times 4.5 \mathrm{~cm}^{2}=9 \mathrm{~cm}^{2} \)
Thus, total area is \( 2.5+6.5+9+1.5=19.5 \mathrm{~sq} \mathrm{~cm} \)
heron's formula class 9 exercise 12.2 || ncert maths class 9 chapter 12 solutions || class 9 maths heron's formula exercise 12.2 || class 9 maths chapter 12 exercise 12.2 || class 9 exercise 12.2 || class 9 math exercise 12.2 || exercise 12.2 class 9 || class 9 maths exercise 12.2 solution
4. A triangle and a parallelogram have the same base and the same
area. If the sides of the triangle are \( 26 \mathrm{~cm}, 28
\mathrm{~cm} \) and 30 cm , and the parallelogram stands on the
base 28 cm , find the height of the parallelogram.
Answer
Given, Area of the parallelogram and triangle are equal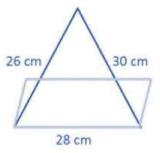
Sides of triangle are \( 26 \mathrm{~cm}, 28 \mathrm{~cm} \) and 30 cm .
Semi perimeter of triangle, \( \mathrm{s}=\frac{26+28+30}{2} \)
\(\mathrm{S}=\frac{84}{2}\)
\(=42 \mathrm{~cm}\)
Using Heron's formula,
Area of triangle \( =\sqrt{s(s-a)(s-b)(s-c)} \)
\(=\sqrt{42(42-26)(42-28)(42-30)}\)
\(=\sqrt{42 \times 16 \times 14 \times 12}\)
\(=336 \mathrm{~cm}^{2}\)
\( = \) Let the height of parallelogram be h ,
As parallelogram and triangle having same base and same height have equal areas.
\( \therefore \) Area of parallelogram \( = \) Area of triangle
\(28 \times \mathrm{h}=336\)
\(\mathrm{h}=\frac{336}{28}\)
\(\mathrm{~h}=12 \mathrm{~cm}\)
Hence, the height of the parallelogram is 12 cm .
5. A rhombus shaped field has green grass for 18 cows to graze.
If each side of the rhombus is 30 m and its longer diagonal is 48
m , how much area of grass field will each cow be getting?
Answer
Diagonals divide the rhombus ABCD into two congruent triangles of
equal area.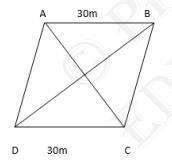
Semi perimeter of \( \triangle A B C=\frac{30+30+48}{2}=54 \mathrm{~m} \)
Using Heron's formula,
\(\text {Area of } \triangle A B C=\sqrt{s(s-a)(s-b)(s-c)}\)
\( \sqrt{54(54-30)(54-30)(54-48)}\)
\(=\sqrt{54 \times 24 \times 24 \times 6}\)
\(=432 \mathrm{~m}^{2}\)
Area of field \( =2 x \) area of field \( \triangle A B C \)
\(=2 \times 432\)
\(=864 \mathrm{~m}^{2}\)
Thus,
Area of grass field which each cow will be getting \( =\frac{864}{18}=48 \mathrm{~m}^{2} \)
6. An umbrella is made by stitching 10 triangular pieces of cloth
of two different colors (see Fig. 12.16), each piece measuring \(
20 \mathrm{~cm}, 50 \) cm and 50 cm . How much cloth of each color
is required for the umbrella?


Answer
To Find: Total Amount of cloth requiredGiven: Umbrella is made up of 10 triangular pieces of sides 50, 50 and 20 cm
Perimeter of each triangular piece of cloth \( =50+50+20 \)
Semi perimeter of each triangular piece of cloth \( =\frac{50+50+20}{2} \)
\(=\frac{120}{2}\)
\(=60 \mathrm{~cm}\)
Using Heron's formula,
Area of one triangular piece \( =\sqrt{s(s-a)(s-b)(s-c)} \)
where, as is the semi-perimeter of the triangle and \( \mathrm{a}, \mathrm{b} \) and c are the sides of the triangle.
\(=\sqrt{60(60-50)(60-50)(60-20)}\)
\(=\sqrt{60 \times 10 \times 10 \times 40}\)
\(=200 \sqrt{6} \mathrm{~cm}^{2}\)
Area of piece of cloth of one colour \( =5 \times 200 \sqrt{ 6} \)
\(=1000 \sqrt{6} \mathrm{~cm}^{2}\)
7. A kite in the shape of a square with a diagonal 32 cm and an
isosceles triangle of base 8 cm and sides 6 cm each is to be made
of three different shades as shown in Fig. 12.17. How much paper
of each shade has been used in it?
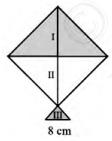

Answer
For I and II section:For calculating the area of the square, Let the length of side \( =x \mathrm{~cm} \)
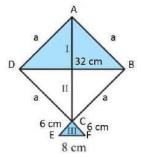
Each Interior Angle of square \( =90^{\circ} \) Pythagoras Theorem: Square of Hypotenuse equals to the sum of squares of other two sides
Now by Pythagoras theorem, \( x^{2}+x^{2}=3^{2} \times 3^{2} \)
\(2 x^{2}=3^{2} \times 3^{2}\)
\(x^{2}=16 \times 32=512 \mathrm{~cm}^{2}\)
Area of Square \( =(\text {side})^{2} \)
And this will be the area of Square.
Area of square \( =512 \mathrm{~cm}^{2} \)
Area of section \( \mathrm{I}= \) Area of section \( \mathrm{I I}=\frac{1}{2} \) Area of square
Now, we need half of this area,
So half of the area of square \( =256 \mathrm{~cm}^{2} \)
For the III section
Length of the sides of triangle \( =6 \mathrm{~cm}, 6 \mathrm{~cm} \) and 8 cm
Perimeter of triangle \( =6+6+8=20 \mathrm{~cm} \)
Semi-Perimeter of Triangle, \( \mathrm{s}=10 \mathrm{~cm} \)
Using Heron's formula,
Area of the III triangular piece \( =\sqrt{s(s-a)(s-b)(s-c)} \)
where, \( \mathrm{s}= \) semi-perimeter and \( \mathrm{a}, \mathrm{b} \), and c are the sides of the triangle
\(\text {Area of Triangle } =\sqrt{10(10-6)(10-6)(10-8)}\)
\( =\sqrt{4 \times 10 \times 2 \times 4}\)
Area of Triangle \( =8 \sqrt{5} \mathrm{~cm}^{2} \)
\(=17.92 \mathrm{~cm}^{2}\)
8 .A floral design on a floor is made up of 16 tiles which are
triangular, the sides of the triangle being \( 9 \mathrm{~cm}, 28
\mathrm{~cm} \) and 35 cm (see Fig. 12.18). Find the cost of
polishing the tiles at the rate of 50p per \( \mathrm{cm}^{2}
\)
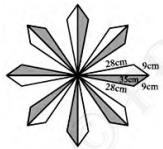

Answer

So, we need to find the area of all 16 tiles or we can say that Area of 16 triangles.
Perimeter of each triangular shaped tiles \( =28+9+35 \)
Semi perimeter of each triangular shaped tiles, \( \mathrm{s}=\frac{28+9+35}{2} \)
\( \mathrm{s}=\frac{72}{2} \)
\( \mathrm{s}=36 \mathrm{~cm} \)
Now,
Using Heron's formula,
Area of each triangular shape \( =\sqrt{s(s-a)(s-b)(s-c)} \)
where \( \mathrm{s}= \) semi perimeter of triangle and \( \mathrm{a}, \mathrm{b}, \mathrm{c} \) are the sides of the triangle
Area of 1 triangular shape \( =\sqrt{36(36-28)(36-9)(36-35)} \)
\( =\sqrt{36 \times 8 \times 1 \times 27} \)
Area of 1 tile \( =36 \sqrt{6} \mathrm{~cm}^{2} \)
Total area of 16 tiles \( =16 \times 36 \sqrt{6} \mathrm{~cm}^{2}=576 \sqrt{6} \mathrm{~cm}^{2} \)
Total Area of 16 tiles \( =576 \times 2.45 \mathrm{~cm}^{2} \)\( \ \ [\sqrt{6}=2.45] \)
Total Area of 16 tiles \( =1411.2 \mathrm{~cm}^{2} \)
Rate of polishing tiles \( =50 \mathrm{~p} \) per \( \mathrm{cm}^{2} \)
Hence,
The total cost of polishing tiles \( =50 \times 1411.2 \)
\( =70560 \) paise As 1 paisa \( =\frac{1}{100} \mathrm{Rs}=\mathrm{RS} .705 .60 \)
9. A field is in the shape of a trapezium whose parallel sides
are 25 m and 10 m . The non-parallel sides are 14 m and 13 m .
Find the area of the field.
Answer
Let ABCD be the given trapezium whoseparallel sides are:
\( \mathrm{AB}=25 \mathrm{~m} \) and \( \mathrm{CD}=10 \mathrm{~m} \)
And,
Non-parallel sides are \( \mathrm{AD}=13 \mathrm{~m} \) and \( \mathrm{BC}=14 \mathrm{~m} \)
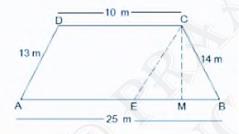
Now,
CM perpendicular to AB and \( \mathrm{CE} \| \mathrm{AD} \)
In \( \triangle B C E \)
\( \mathrm{BC}=14 \mathrm{~m}, \mathrm{CE}=\mathrm{AD}=13 \mathrm{~m} \) and
\( \mathrm{BE}=\mathrm{AB}-\mathrm{AE} \)
\( =25-10 \)
\( =15 \mathrm{~m} \)
Semi perimeter of \( \triangle B C E=\frac{15+13+14}{2} \)
\(=\frac{42}{2}\)
\( =21 \mathrm{~cm} \)
Now,
Using Heron's formula,
Area of \( \triangle B C E=\sqrt{s(s-a)(s-b)(s-c)} \)
where, \( \mathrm{s}= \) semi perimeter, \( \mathrm{a}, \mathrm{b} \) and c are the sides of the triangle.
\(=\sqrt{21(21-15)(21-13)(21-14)}\)
\(=\sqrt{21 \times 8 \times 6 \times 7}\)
\(=84 \mathrm{~m}^{2}\)
Now from \( \Delta \) CEB, Area of triangle \( =\frac{ 1 }{ 2 } \times \) base \(\times\) height
For CEB, CM will be the height and 15 cm will be base of the triangle.
And we calculated the area from above. So,
\(\frac{1}{2} \times 15 \times \mathrm{CM}=84\)
\(\mathrm{CM}=\frac{56}{5} \mathrm{~m}\)
Area of parallelogram \( \mathrm{AECD}= \) Base \( \times \) Altitude
\(=\mathrm{AE} \times \mathrm{CM}\)
\(=10 \times \frac{56}{5}\)
\(=112 \mathrm{~m}^{2}\)
Area of trapezium \( \mathrm{ABCD}= \) Area of AECD + Area of triangle BCE
\(=(112+84) \mathrm{m}^{2}\)
\(=196 \mathrm{~m}^{2}\)

