Ex 10.1 class 12 maths ncert solutions | class 12 maths exercise 10.1 | class 12 maths ncert solutions chapter 10 exercise 10.1 | exercise 10.1 class 12 maths ncert solutions | class 12 maths chapter 10 ncert solutions | class 12 chapter 10 maths ncert solutions | vector algebra class 12 ncert solutions
Explore the complete and accurate Ex 10.1 Class 12 Maths NCERT Solutions to get a strong grip on the fundamentals of vectors. This exercise is part of Class 12 Maths Chapter 10 NCERT Solutions, focusing on the basics of vector quantities, magnitude, and direction. Our step-by-step Class 12 Maths Exercise 10.1 solutions simplify concepts, making learning easier for students. With clear explanations and solved examples, the Exercise 10.1 Class 12 Maths NCERT Solutions help you understand how to represent vectors geometrically and algebraically. Strengthen your preparation with these trusted Class 12 Chapter 10 Maths NCERT Solutions, which are part of the broader Vector Algebra Class 12 NCERT Solutions—a crucial topic for both board exams and competitive tests.
ex 10.1 class 12 maths ncert solutions || vector algebra class 12 ncert solutions || class 12 maths exercise 10.1 || class 12 chapter 10 maths ncert solutions || class 12 maths chapter 10 ncert solutions || exercise 10.1 class 12 maths ncert solutions || class 12 maths ncert solutions chapter 10 exercise 10.1
Exercise 10.1
1. Represent graphically a displacement of \( 40 \mathrm{~km}, 30^{\circ} \) east of north.
Answer
North (N), South (S), East (E), and West (W) are plotted on the paper as shown.
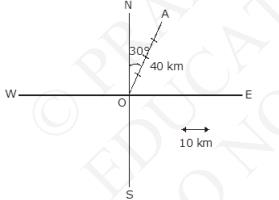
Let \( \overrightarrow{\mathrm{OA}} \) be the displacement vector such that \( |\overrightarrow{\mathrm{OA}}|=40 \mathrm{~km} \)
Vector \( |\overrightarrow{O A}| \) makes an angle of \( 30^{\circ} \) east of North i.e. \( 30^{\circ} \) with North in North-East direction
2. Classify the following measures as scalars and vectors.
(i) 10 kg
Answer
Scalars are defined as quantities that have magnitude only.
Vectors are defined as a quantity that has magnitude as well as direction.
\( \mathbf{1 0} \mathbf{~ k g} \) : It is a measure of mass. It is a scalar quantity as it has magnitude only and no direction.
ex 10.1 class 12 maths ncert solutions || vector algebra class 12 ncert solutions || class 12 maths exercise 10.1 || class 12 chapter 10 maths ncert solutions || class 12 maths chapter 10 ncert solutions || exercise 10.1 class 12 maths ncert solutions || class 12 maths ncert solutions chapter 10 exercise 10.1
(ii) 2 meters north-west
Answer
Scalars are defined as quantities that have magnitude only.
Vectors are defined as a quantity that has magnitude as well as direction.
2 meters north-west: It is a measure of distance in a particular direction. \( \therefore \) It is a vector quantity as it has magnitude as well as direction.
(iii) \( 40^{\circ} \)
Answer
Scalars are defined as quantities that have magnitude only.
Vectors are defined as a quantity that has magnitude as well as direction.
\( 40^{\circ} \) : It is a measure of angle. It is a scalar quantity as it has magnitude only and no direction.
(iv) 40 watt
Answer
Scalars are defined as quantities that have magnitude only.
Vectors are defined as a quantity that has magnitude as well as direction.
40 Watt: It is a measure of power. It is a scalar quantity as it has magnitude only and no direction.
ex 10.1 class 12 maths ncert solutions || vector algebra class 12 ncert solutions || class 12 maths exercise 10.1 || class 12 chapter 10 maths ncert solutions || class 12 maths chapter 10 ncert solutions || exercise 10.1 class 12 maths ncert solutions || class 12 maths ncert solutions chapter 10 exercise 10.1
(v) \( 10^{-19} \) coulomb
Answer
Scalars are defined as quantities that have magnitude only.
Vectors are defined as a quantity that has magnitude as well as direction.
\( \mathbf{1 0}^{\mathbf{- 1 9}} \) coulomb: It is a measure of electric charge. It is a scalar quantity as it has magnitude only and no direction.
(vi) \( 20 \mathrm{~m} / \mathrm{s}^{2} \)
Answer
Scalars are defined as quantities that have magnitude only.
Vectors are defined as a quantity that has magnitude as well as direction.
\( \mathbf{2 0} \mathbf{~ m} / \mathbf{s e c}^{\mathbf{2}} \) : It is a measure of acceleration. It is a vector quantity as it is a measure of rate of change of velocity.
3. Classify the following as scalar and vector quantities.
(i) time period
Answer
Scalars are defined as quantities that have magnitude only.
Vectors are defined as a quantity that has magnitude as well as direction.
time period: It is a scalar quantity as it has magnitude only and no direction.
(ii) distance
Answer
Scalars are defined as quantities that have magnitude only.
Vectors are defined as a quantity that has magnitude as well as direction.
distance: It is a scalar quantity as it has magnitude only and no direction.
(iii) force
Answer
Scalars are defined as quantities that have magnitude only.
Vectors are defined as a quantity that has magnitude as well as direction.
force: It is a vector quantity as it has magnitude as well as direction.
(iv) velocity
Answer
Scalars are defined as quantities that have magnitude only.
Vectors are defined as a quantity that has magnitude as well as direction.
velocity: It is a vector quantity as it has magnitude as well as direction.
(v) work done
Answer
Scalars are defined as quantities that have magnitude only.
Vectors are defined as a quantity that has magnitude as well as direction.
work done: It is a scalar quantity as it has magnitude as well as direction.
ex 10.1 class 12 maths ncert solutions || vector algebra class 12 ncert solutions || class 12 maths exercise 10.1 || class 12 chapter 10 maths ncert solutions || class 12 maths chapter 10 ncert solutions || exercise 10.1 class 12 maths ncert solutions || class 12 maths ncert solutions chapter 10 exercise 10.1
4. In Fig 10.6 (a square), identify the following vectors.
(i) Coinitial
(ii) Equal
(iii) Collinear but not equal
(i) Coinitial
(ii) Equal
(iii) Collinear but not equal
Answer
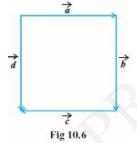
(i) Coinitial vectors: Two or more vectors having same initial point are called coinitial vectors.
So, in the above figure \( \overrightarrow{a} \) and \( \overrightarrow{d} \) are Coinitial vectors as they have same initial point.
\( \therefore \) Coinitial vectors: \( \overrightarrow{a} \) and \( \overrightarrow{d} \)
(ii) Equal vectors: Two or more vectors having same direction and same magnitude are called equal vectors.
So, in the above figure \( \overrightarrow{b} \) and \( \overrightarrow{d} \) are equal vectors as they have same magnitude and same direction.
\( \therefore \) Equal vectors: \( \overrightarrow{b} \) and \( \overrightarrow{d} \)
(iii) Collinear but not equal:
\( \because \overrightarrow{a} \) and \( \overrightarrow{c} \) are parallel vectors, so, they are collinear. But they have opposite direction, so, they are not equal.
Hence, \( \overrightarrow{a} \) and \( \overrightarrow{c} \) are collinear but not equal.
5. Answer the following as true or false.
(i) \( \overrightarrow{a} \) and \( -\overrightarrow{a} \) are collinear.
Answer
\( \overrightarrow{a} \) and \( -\overrightarrow{a} \) are collinear: True
Explanation: \( \overrightarrow{a} \) and \( -\overrightarrow{a} \) are parallel vectors, so, they are collinear.
(ii) Two collinear vectors are always equal in magnitude.
Answer
Two collinear vectors are always equal in magnitude: False
Explanation: we know, \(\hat{i}\) and \( \hat{j} \) are unit vectors, so they have same magnitude but and are vectors along \(x- \) axis and \(y- \) axis respectively.
(iii) Two vectors having same magnitude are collinear.
Answer
Two vectors having same magnitude are collinear: False
Explanation: Two or more vectors are said to be collinear if they are parallel to the same line, irrespective of their magnitudes and directions. We know, \(\hat{i}\) and \( \hat{j} \) are unit vectors, so they have same magnitude but and are vectors along \(x\) - axis and \(y\) - axis respectively. Since, they are not parallel to each other, so, they are not collinear.
(iv) Two collinear vectors having the same magnitude are equal.
Answer
Two collinear vectors having the same magnitude are equal: False
Explanation: Two vector are said to be equal, if they have the same magnitude and direction.
\( \overrightarrow{b} \) and \( -\overrightarrow{b} \) are collinear vectors as they are parallel to each other and also they have same magnitude. But they do not have same direction, so, they are unequal vectors.
