Ex 12.1 class 12 maths ncert solutions | class 12 maths exercise 12.1 | class 12 maths ncert solutions chapter 12 exercise 12.1 | exercise 12.1 class 12 maths ncert solutions | class 12 maths chapter 12 ncert solutions | class 12 chapter 12 maths ncert solutions | ncert solutions for class 12 maths ch 12 | ncert solutions for class 12 maths chapter 12 | linear programming class 12 ncert solutions
Looking to solve Linear Programming problems with accuracy and confidence? The Class 12 Maths NCERT Solutions Chapter 12 Exercise 12.1 is your perfect guide to understanding how to frame and solve linear inequalities for real-life situations. Whether you’re searching for Class 12 Maths Exercise 12.1, Exercise 12.1 Class 12 Maths NCERT Solutions, or the complete NCERT Solutions for Class 12 Maths Chapter 12, this resource provides simple, step-by-step explanations that help you visualize constraints graphically and find optimal solutions. With the Linear Programming Class 12 NCERT Solutions, tackling optimization problems becomes not just easy, but enjoyable and highly scoring.

linear programming class 12 ncert solutions || class 12 chapter 12 maths ncert solutions || ex 12.1 class 12 maths ncert solutions || class 12 maths chapter 12 ncert solutions || ncert solutions for class 12 maths chapter 12 || class 12 maths ncert solutions chapter 12 exercise 12.1 || class 12 maths exercise 12.1 || ncert solutions for class 12 maths ch 12 || exercise 12.1 class 12 maths ncert solutions
Exercise 12.1
1. Maximise \( Z=3 x+4 y \) subject to the constraints : \( x+y \leq 4, x \geq 0, y \) \( \geq 0 \).
Answer
It is given in the question that,
\(Z=3 x+4 y\)
We have to subject on the following equation:
\(x \geq 0, y \geq 0, x+y \leq 4\)
\(\begin{array}{|l|l|l|}
\hline x & 0 & 4\\
\hline y & 4 & 0\\
\hline
\end{array}\)
\((x, y)=(0,4),(4,0)\)
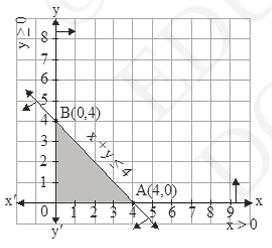
Corner points Value of \( Z=3 x+4 y \)
\( (0,4) \quad 16 \)
\( (4,0) \quad 12 \)
\( (0,0) \quad 0\)
\( \text {We can clearly see that \( Z \) is maximum at} (0,4) \). \(\text{Hence, maximum value of Z will be }16\)
linear programming class 12 ncert solutions || class 12 chapter 12 maths ncert solutions || ex 12.1 class 12 maths ncert solutions || class 12 maths chapter 12 ncert solutions || ncert solutions for class 12 maths chapter 12 || class 12 maths ncert solutions chapter 12 exercise 12.1 || class 12 maths exercise 12.1 || ncert solutions for class 12 maths ch 12 || exercise 12.1 class 12 maths ncert solutions
2. Minimise \( Z=-3 x+4 y \) subject to \( x+2 y \leq 8,3 x+2 y \leq 12 \), \( x \geq 0 \), \( y \geq 0 \).
Answer
It is given in the question that,
\(Z=-3 x+4 y\)
We have to subject on the following equation:
\(x+2 y \leq 8,3 x+2 y \leq 12, x \geq 0, y \leq 0\)
\(3 x+2 y \leq 12\)
\(\begin{array}{|l|l|l|}
\hline x & 0 & 4 \\
\hline y & 6 & 0 \\
\hline
\end{array}\)
\(\begin{array}{l}
(x, y)=(0,6),(4,0) \\
x+2 y \leq 8
\end{array}\)
\(\begin{array}{|l|l|l|}
\hline x & 0 & 8 \\
\hline y & 4 & 0 \\
\hline
\end{array}\)
\((x, y)=(0,4),(8,0)\)
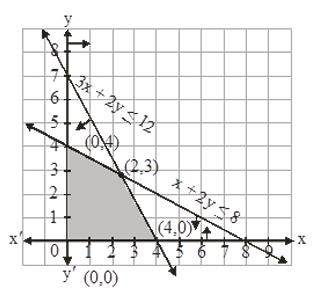
\(\begin{array}{|l|l|}
\hline Corner \ points & Value \ of \ 2 \\
\hline (0,4) & 16 \\
\hline (2,3) & -6 \\
\hline (4,0) & 12 \\
\hline
\end{array}\)
\( \text{We can clearly see that Z is minimum at }(4,0) \). \(\text{Hence, minimum value of Z will be} -12\)
3. Maximise \( Z=5 x+3 y \) subject to \( 3 x+5 y \leq 15,5 x+2 y \leq 10, x \geq 0 \), \( y \geq 0 \).
Answer
It is given in the question that,
\(Z=5 x+3 y\)
We have to subject on the following equation:
\(3 x+5 y \leq 15,5 x+2 y \leq 10, x \geq 0, y \leq 0\)
\(5 x+2 y \leq 10\)
\(\begin{array}{|l|l|l|}
\hline x & 0 & 2 \\
\hline y & 5 & 0 \\
\hline
\end{array} \)
\((x, y)=(0,5),(2,0)\)
\(3 x+5 y \leq 15\)
\(\begin{array}{|l|l|l|}
\hline x & 0 & 5 \\
\hline y & 3 & 0 \\
\hline
\end{array}\)
\((x, y)=(0,3),(5,0)\)
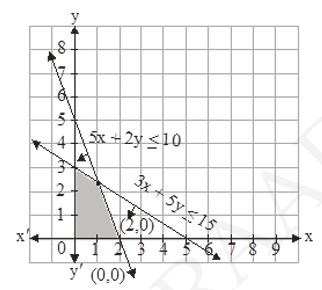
\(\begin{array}{|l|l|}
\hline Corner \ points & Value \ of \ Z \\
\hline (0,3) & 9 \\
\hline \left(\frac{20}{19}, \frac{45}{19}\right) & \frac{235}{19}=12.36 \\
\hline (2,0) & 10 \\
\hline
\end{array}\)
\( \text{We can clearly see that Z is maximum at }\left(\frac{20}{19}, \frac{45}{19}\right) \). \( \text {Hence, maximum value of \( Z \) will be } \frac{235}{19}=12.36 \)
4. Minimize \( z=3 x+5 y \) such that \( x+3 y \geq 3, x+y \geq 2, x, y \geq 0 \).
Answer
It is given in the question that,
\(Z=3 x+5 y\)
We have to subject on the following equation:
\(x+3 y \geq 3, x+2 y \geq 2, x \geq 0, y \leq 0\)
\(x+y \geq 2\)
\(\begin{array}{|l|l|l|}
\hline x & 0 & 2 \\
\hline y & 2 & 0 \\
\hline
\end{array}\)
\((x, y)=(0,2),(2,0)\)
\(x+3 y \geq 3\)
\(\begin{array}{|l|l|l|}
\hline x & 0 & 3 \\
\hline y & 1 & 0 \\
\hline
\end{array}\)
\((x, y)=(0,1),(3,0)\)
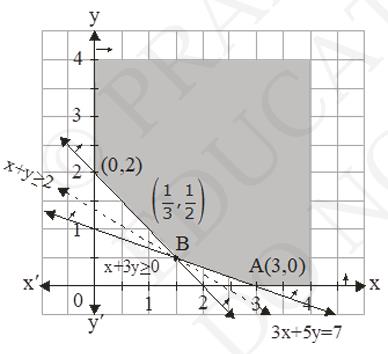
We can clearly see that the feasible region is unbounded and the corner points of the feasible region are \( (3,0),\left(\frac{3}{2}, \frac{1}{2}\right) \) and \( (0,2) \)
\(\begin{array}{|l|l|}
\hline \text {Corner points} & \text {Value of } Z \\
\hline (0,2) & 10 \\
\hline \left(\frac{3}{2}, \frac{1}{2}\right) & 7 \\
\hline (3,0) & 9 \\
\hline
\end{array}\)
As per the table minimum value of Z is 7 but we can see that the feasible region is unbounded. Thus, 7 may or may not be the minimum value of Z
\( \therefore \) We will plot the graph of inequality, \( 3 x+5 y < 7 \)
Here we will see is the resulting half plane has common points with the feasible region or not. As per the graph we can observe that the feasible region has no points in common with \( 3 x+5 y < 7 \).
Hence, the minimum value of 7 is at \( \left(\frac{3}{2}, \frac{1}{2}\right) \) which is 7 .
5. Maximize \( z=3 x+2 y \) subject to \( x+2 y \leq 10,3 x+y \leq 15, x, y \geq 0 \).
Answer
It is given in the question that,
\(Z=3 x+2 y\)
We have to subject on the following equation:
\(x+2 y \leq 10,3 x+y \leq 15, x, y \geq 0\)
\(3 x+y \leq 15\)
\(\begin{array}{|l|l|l|}
\hline X & 0 & 5 \\
\hline Y & 15 & 0 \\
\hline
\end{array}\)
\((x, y)=(0,15),(5,0)\)
\(x+2 y \leq 10\)
\(\begin{array}{|l|l|l|}
\hline X & 0 & 10 \\
\hline Y & 5 & 0 \\
\hline
\end{array}\)
\((x, y)=(0,5),(10,0)\)
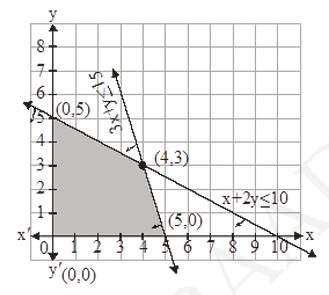
\(\begin{array}{|l|l|}
\hline Corner \ points & Value \ of \ Z \\
\hline (5,0) & 15 \\
\hline (4,3) & 18 \\
\hline (0,5) & 10 \\
\hline (0,0) & 0 \\
\hline
\end{array}\)
We can clearly see that \( Z \) is maximum at \( (4,3) \). Hence, maximum value of Z will be 18
6. Minimize \( z=x+2 y \) subject to \( 2 x+y \geq 3, x+2 y \geq 6, x, y \geq 0 \). Show that the minimum of \( Z \) occurs at more than two points.
Answer
It is given in the question that,
\(z=x+2 y\)
We have to subject on the following equation:
\(2 x+y \geq 3, x+2 y \geq 6, x, y \geq 0\)
\(x+2 y \geq 6\)
\(\begin{array}{|l|l|l|}
\hline X & 0 & 6 \\
\hline Y & 3 & 0 \\
\hline
\end{array}\)
\((x, y)=(0,3),(6,0)\)
\(2 x+y \geq 3\)
\(\begin{array}{|l|l|l|}
\hline X & 0 & 1 \\
\hline Y & 3 & 1 \\
\hline
\end{array}\)
\((x, y)=(0,3),(1,1)\)
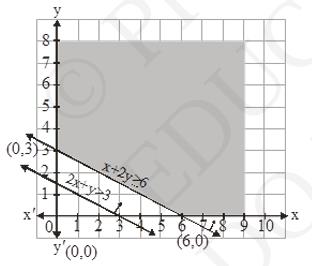
\(\begin{array}{|l|l|}
\hline \begin{array}{l}
Corner \\
points
\end{array} & \begin{array}{l}
Value \ of \\
\mathbf{Z}
\end{array} \\
\hline (0,3) & 6 \\
\hline (6,0) & 6 \\
\hline
\end{array}\)
As per the table minimum value of \( Z \) is 6 but we can see that the feasible region is unbounded. Thus, 6 may or may not be the minimum value of Z
\( \therefore \) We will plot the graph of inequality,
Here we will see that there is no common point with the feasible region.
Hence, Z will be minimum on all points joining line \( (0,3),(6,0) \).
Therefore, \( Z \) will be minimum on \( x+2 y=6 \)
7. Minimize and Maximize \( Z=5 x+10 y \) subject to \( x+2 y \leq 120, x+ \) \( y \geq 60, x-2 y \geq 0, x, y \geq 0 \).
Answer
It is given in the question that,
Minimize and Maximize, \( Z=5 x+10 y \)
We have to subject on the following equation:
\(x+2 y \leq 120, x+y \geq 60, x-2 y \geq 0, x, y \geq 0\)
\(x+2 y \leq 120\)
\(\begin{array}{|l|l|l|}
\hline X & 0 & 120 \\
\hline Y & 60 & 0 \\
\hline
\end{array}\)
\((x, y)=(0,60),(120,0)\)
\(x-2 y \geq 0\)
\(\begin{array}{|l|l|l|}
\hline X & 0 & 20 \\
\hline Y & 0 & 10 \\
\hline
\end{array}\)
\((x, y)=(0,0),(20,10)\)
\(x+y \geq 60\)
\(\begin{array}{|l|l|l|}
\hline X & 60 & 0 \\
\hline Y & 0 & 60 \\
\hline
\end{array}\)
\((x, y)=(60,0),(0,60)\)
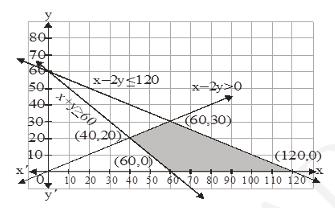
\(\begin{array}{|l|l|}
\hline Corner \ points & Value \ of \ Z \\
\hline (60,30) & 600 \\
\hline (40,20) & 400 \\
\hline (60,0) & 300 \\
\hline (120,0) & 600 \\
\hline
\end{array}\)
\( \therefore \) It is clear that at \( (60,0) z \) has its minimum value i.e. 300
Also, Z is minimum at two pints \( (60,30) \) and \( (120,0) \)
Hence, the value of Z will be maximum at all points joining \( (60,30) \) and \( (120,0) \)
8. Minimize and Maximize \( z=x+2 y \) subject to \( x+2 y \geq 100,2 x-y \) \( \leq 0,2 x+y \leq 200 ; x, y \geq 0 \).
Answer
It is given in the question that,
Minimize and Maximize, \( z=x+2 y \)
We have to subject on the following equation:
\(x+2 y \geq 100,2 x-y \leq 0,2 x+y \leq 200 ; x, y \geq 0\)
\(2 x+y \leq 200\)
\(\begin{array}{|l|l|l|}
\hline X & 0 & 100 \\
\hline Y & 50 & 0 \\
\hline
\end{array}\)
\((x, y)=(0,50),(100,0)\)
\(2 x-y \leq 0\)
\(\begin{array}{|l|l|l|}
\hline X & 0 & 50 \\
\hline Y & 0 & 100 \\
\hline
\end{array}\)
\((x, y)=(0,0),(50,100)\)
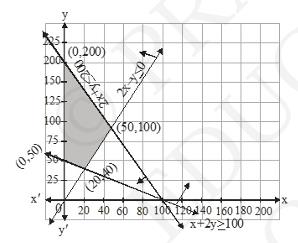
\(\begin{array}{|l|l|}
\hline Corner \ points & Value \ of \ Z \\
\hline (0,200) & 400 \\
\hline (0,50) & 100 \\
\hline (20,40) & 100 \\
\hline (50,100) & 250 \\
\hline
\end{array} \)
\( \therefore \) It is clear that at \( (0,200) z \) has its maximum value i.e. 400
Also, Z is minimum at two pints \( (0,50) \) and \( (20,40) \)
Hence, the value of \( Z \) will be minimum at all points joining \( (0,50) \) and \( (20,40) \)
9. Maximize \( Z=-x+2 y \), subject to the constraints: \( x \geq 3, x+y \geq 5, x \) \( +2 y \geq 6, y \geq 0 \).
Answer
It is given in the question that,
\(Z=-x+2 y\)
We have to subject on the following equation:
\(x \geq 3, x+y \geq 5, x+2 y \geq 6, y \geq 0\)
\(x+y \geq 5\)
\(\begin{array}{|l|l|l|}
\hline X & 5 & 0 \\
\hline Y & 0 & 5 \\
\hline
\end{array}\)
\((x, y)=(5,0),(0,5)\)
\(x+2 y \geq 6\)
\(\begin{array}{|l|l|l|}
\hline X & 6 & 0 \\
\hline Y & 0 & 3 \\
\hline
\end{array}\)
\((x, y)=(6,0),(3,0)\)
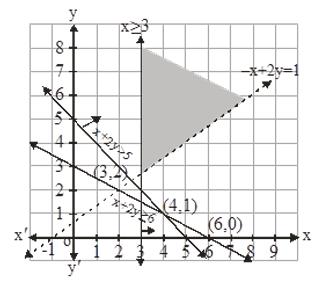
We can clearly see that the feasible region is unbounded and the corner points of the feasible region are \( (3,2),(4,1) \) and \( (6,0) \)
\(\begin{array}{|l|l|}
\hline Corner \ points & Value \ of \ Z \\
\hline (3,2) & 1 \\
\hline (4,1) & -2 \\
\hline (6,0) & -6 \\
\hline
\end{array}\)
As per the table maximum value of \( Z \) is 1 but we can see that the feasible region is unbounded. Thus, 1 may or may not be the minimum value of \( Z \)
\( \therefore \) We will plot the graph of inequality, \( x+2 y \geq 1 \)
Here we will see is the resulting half plane has common points with the feasible region or not. As per the graph we can observe that the feasible region have some points in common with \( -x+2 y > 1 \).
Hence, there is no maximum value of \( Z \)
10. Maximize \( z=x+y \), subject to \( x-y \leq-1,-x+y \leq 0, x, y \geq 0 \).
Answer
It is given in the question that,
\(Z=x+y\)
We have to subject on the following equation:
\(x-y \leq-1,-x+y \leq 0, x, y \geq 0\)
\(x-y \leq-1\)
\(\begin{array}{|l|l|l|}
\hline X & 0 & -1 \\
\hline Y & 1 & 0 \\
\hline
\end{array}\)
\((x, y)=(0,1),(-1,0)\)
\(-x+y \leq 0\)
\(\begin{array}{|l|l|l|}
\hline X & 0 & 1 \\
\hline Y & 0 & 0 \\
\hline
\end{array}\)
\((x, y)=(0,0),(1,1)\)
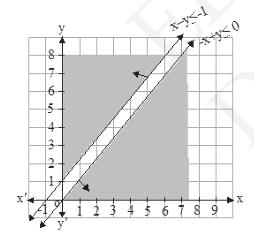
From the above graph it is clear that, there is no common region or say feasible region. Hence, for the given condition Z has no maximum value.
