Ex 8.1 Class 12 Maths Ncert Solutions

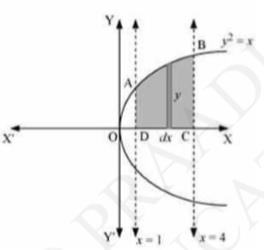
We can see from the figure that the area of the region bounded by the curve \( y^{2}=x \) and the lines \( x=1, x=4 \) is shown by shaded region that is Area ABCD.
Area of \( \mathrm{ABCD}=\int_{1}^{4} y d y=\int_{1}^{4} \sqrt{x} d x \)
\(
=\left[\frac{x^{\frac{3}{2}}}{\frac{3}{2}}\right]_{1}^{4}=\frac{2}{3}\left[(4)^{\frac{3}{2}}-(1)^{\frac{3}{2}}\right]\)
\(=\frac{2}{3}[8-1]\)
\(=\frac{14}{3} \text { units }
\)

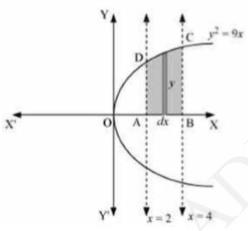
We can see from the figure that the area of the region bounded by the curve \( y^{2}=9 x, x=2, x=4 \) is shown by shaded region that is Area ABCD.
Area of \( \mathrm{ABCD}=\int_{2}^{4} y d y=3 \int_{2}^{4} \sqrt{x} d x \)
\( =3\left[\frac{x^{\frac{3}{2}}}{\frac{3}{2}}\right]_{2}^{4}=2\left[(4)^{\frac{3}{2}}-(1)^{\frac{3}{2}}\right] \)
\( =\frac{2}{3}[8-2 \sqrt{2}] \)
\( =(16-4 \sqrt{2}) \) units

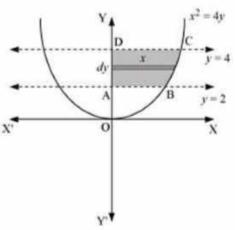
We can see from the figure that the area of the region bounded by the curve \( x^{2}=4 y, y=2, y=4 \) is shown by shaded region that is Area ABCD.
Area of \( \mathrm{ABCD}=\int_{2}^{4} y d y=2 \int_{2}^{4} \sqrt{y} d y \)
\( =2\left[\frac{y^{\frac{3}{2}}}{\frac{3}{2}}\right]_{2}^{4}=2\left[(4)^{\frac{3}{2}}-(2)^{\frac{3}{2}}\right] \)
\( =\frac{4}{3}[8-2 \sqrt{2}] \)
\( =\left(\frac{32-8 \sqrt{2}}{3}\right) \) units

It is given that equation of ellipse is \( \frac{x^{2}}{16}+\frac{y^{2}}{9}=1 \)
We can see that the ellipse is symmetrical about x -axis and y -axis.
\( \therefore \) Area bounded by ellipse \( =4 \times \) Area of OAB
\( \text{Area of} \ \mathrm{ABCD}=\int_{0}^{4} y d x=\int_{0}^{4} 3 \sqrt{1-\frac{x^{2}}{16} d x}=\frac{3}{4} \int_{0}^{4} \sqrt{16-x^{2}} d x \)
\(
=\frac{3}{4}\left[\frac{x}{2} \sqrt{16-x^{2}}+\frac{16}{2} \sin ^{-1} \frac{x}{4}\right]_{0}^{4}\)
\(=\frac{3}{4}\left[2 \sqrt{16-16}+8 \sin ^{-1}(1)-0-8 \sin ^{-1}(0)\right]\)
\(=\frac{3}{4}\left[\frac{8 \pi}{2}\right]\)
\(=\frac{3}{4}[4 \pi]\)
\(=3 \pi\)
Therefore, the required area bounded by the ellipse \( =4 \times 3 \pi=12 \pi \) units.

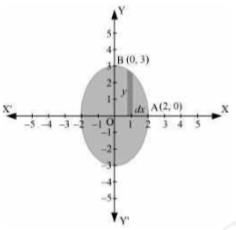
It is given that equation of ellipse is \( \frac{x^{2}}{4}+\frac{y^{2}}{9}=1 \)
We can see that the ellipse is symmetrical about \( x- \) axis and y -axis.
\( \therefore \) Area bounded by ellipse \( =4 \times \) Area of OAB
Area of \( \mathrm{ABCD}=\int_{0}^{2} y d x=\int_{0}^{2} 3 \sqrt{1-\frac{x^{2}}{4}} d x \)
\(=\frac{3}{2} \int_{0}^{2} \sqrt{4-x^{2}} d x\)
\(=\frac{3}{2}\left[\frac{x}{2} \sqrt{4-x^{2}}+\frac{4}{2} \sin ^{-1} \frac{x}{4}\right]_{0}^{2}\)
\(=\frac{3}{2}\left[\frac{2 \pi}{2}\right]\)
\(=\frac{3 \pi}{2}\)
Therefore, the required area bounded by the ellipse \( =4 \times \frac{3 \pi}{2}=6 \pi \) units.

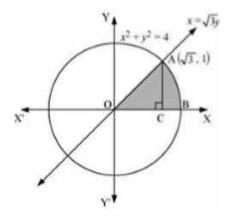
The equations are \( x=\sqrt{3} y \) and the circle \( x^{2}+y^{2}=4 \)
From the figure we can see that the \( x \)-axis is the area \( O A B \) and it is shown by shaded region.
Now, the point of intersection of the line and the circle in the first quadrant is \( (\sqrt{3}, 1) \).
Area \( \mathrm{OAB}= \) Area \( \triangle \mathrm{OCA}+ \) Area ACB
Area of \( \triangle \mathrm{OCA}=\frac{1}{2} \times O C \times A C=\frac{1}{2} \times \sqrt{3} \times 1=\frac{\sqrt{3}}{2} \)
Also,
Area of \( \mathrm{ABC}=\int_{\sqrt{3}}^{2} y d x=\int_{\sqrt{3}}^{2} \sqrt{4-x^{2}} d x \)
\(=\left[\frac{x}{2} \sqrt{4-x^{2}}+\frac{4}{2} \sin ^{-1} \frac{x}{2}\right]_{\sqrt{3}}^{2}\)
\(=\left[\pi-\frac{\sqrt{3} \pi}{2} \sqrt{4-3}-2 \sin ^{-1}\left(\frac{\sqrt{3}}{2}\right)\right]\)
\(=\left[\pi-\frac{\sqrt{3}}{2}-2\left(\frac{\pi}{3}\right)\right]\)
\(=\left[\pi-\frac{\sqrt{3}}{2}-\frac{2 \pi}{3}\right]\)
\(=\left[\frac{\pi}{3}-\frac{\sqrt{3}}{2}\right]\)
Therefore, required area is \( =\frac{\sqrt{3}}{2}+\frac{\pi}{3}-\frac{\sqrt{3}}{2}=\frac{\pi}{3} \) square units.

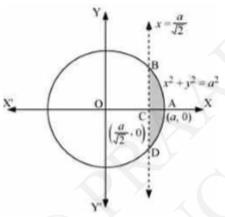
It is given that the area of the smaller part of the circle \( x^{2}+y^{2}=a^{2} \) cut off by the line \( x=\frac{a}{\sqrt{2}} \)
From the figure we can see that the area is ABCDA and it is shown by shaded region.
Now, we can have observed that the area ABCD is symmetrical about x-axis.
Area \( \mathrm{ABCD}=2 \times \) Area \( A B C \)
Area of \( \mathrm{ABC}=\int_{\frac{a}{\sqrt{2}}}^{a} y d x=\int_{\frac{a}{\sqrt{2}}}^{a} \sqrt{a^{2}-x^{2}} d x \)
\(=\left[\frac{x}{2} \sqrt{a^{2}-x^{2}}+\frac{a^{2}}{2} \sin ^{-1} \frac{x}{a}\right]_{\frac{a}{\sqrt{2}}}^{a}\)
\(=\left[\frac{a^{2}}{2}\left(\frac{\pi}{2}\right)-\frac{a}{2 \sqrt{2}} \sqrt{a^{2}-\frac{a^{2}}{2}}-\frac{a^{2}}{2} \sin ^{-1}\left(\frac{1}{\sqrt{2}}\right)\right]\)
\(=\left[\frac{a^{2} \pi}{4}-\frac{a}{2 \sqrt{2}} \cdot \frac{a}{\sqrt{2}}-\frac{a^{2}}{2}\left(\frac{\pi}{4}\right)\right]\)
\(=\frac{a^{2} \pi}{4}-\frac{a^{2}}{4}-\frac{a^{2} \pi}{8}\)
\(=\frac{a^{2}}{4}\left[\pi-1-\frac{\pi}{2}\right]\)
\(=\frac{a^{2}}{4}\left[\frac{\pi}{2}-1\right]\)
\(\Rightarrow \text { Area of ABC }=2\left[\frac{a^{2}}{4}\left(\frac{\pi}{2}-1\right)\right]\)
\(=\frac{a^{2}}{4}\left(\frac{\pi}{2}-1\right)\)
Therefore, required area is \( =\frac{a^{2}}{4}\left(\frac{\pi}{2}-1\right) \) square units

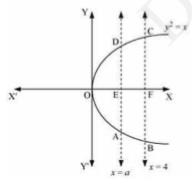
It is given that the area between \( x=y^{2} \) and \( x=4 \) is divided into two equal parts by the line \( x=\mathrm{a} \).
Thus, Area \( \mathrm{OAD}= \) Area ABCD
Now, we can observe that the given area is symmetrical about x -axis.
\( \Rightarrow \) Area OED \( = \) Area EFCD
Now, Area of OED \( =\int_{0}^{a} y d x=\int_{0}^{a} \sqrt{x} d x \)
\( =\left[\frac{x^{\frac{3}{2}}}{\frac{3}{2}}\right]_{0}^{a}=\frac{2}{3}(a)^{\frac{3}{2}} \ldots (1)\)
Area of \( \mathrm{EFCD}=\int_{a}^{4} y d y=\int_{a}^{4} \sqrt{x} d x \)
\(=\left[\frac{x^{\frac{3}{2}}}{\frac{3}{2}}\right]_{a}^{4}=\frac{2}{3}\left[8-(a)^{\frac{3}{2}}\right] \ldots (2)\)
Therefore, from equations (1) and (2), we get,
\( \Rightarrow 2 .(a)^{\frac{3}{2}}=8 \)
\( \mathrm{a}=(4)^{\frac{ 2 }{ 3 }} \)
Hence, the required value of a is \( (4)^{\frac{ 2 }{ 3 }} \).

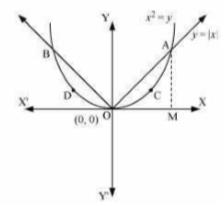
It is given that the area of the region bounded by the parabola \( y=x^{2} \) and \( y=|x| \).
Now, we can observe that the given area is symmetrical about \( y \)-axis.
\( \Rightarrow \) Area \( \mathrm{OACO}= \) Area ODBO
And the point of intersection of parabola, \( y=x^{2} \) and \( y=x \) is \( \mathrm{A}(1,1) \).
Thus, Area \( \mathrm{OACO}= \) Area \( \triangle \mathrm{OAM}- \) Area OMACO
Now, Area of \( \triangle \mathrm{OAM}=\frac{1}{2} \times O M \times A M=\frac{1}{2} \times 1 \times 1=\frac{1}{2} \)
Area of OMACO \( =\int_{0}^{1} y d x=\int_{0}^{1} x^{2} d x \)
\( =\left[\frac{x^{3}}{3}\right]_{0}^{1}=\frac{1}{3} \)
\( \Rightarrow \) Area \( \mathrm{OACO}= \) Area \( \triangle \mathrm{OAM}- \) Area OMACO
\(=\frac{1}{2}-\frac{1}{3}=\frac{1}{6}\)
Therefore, the required area is \( =2 (\frac {1}{6})= \frac {1} {3} \) Answer.

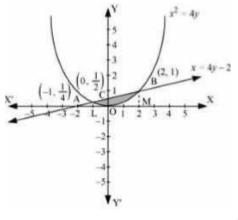
It is given that the area of the region bounded by the parabola \( x^{2}=4 y \) and \( x=4 y-2 \).
Let A and B be the points of intersection of the line and parabola.
Let us calculate the point of intersection of both the curves,
Given: \( x^{2}=4 y \) and \( x=4 y-2 \)
Therefore, putting the value of \( x \), equation of parabola, we get, \( (4 y-2)^{2} \) \( =4 y \)
\( 16 y^{2}+4-16 y=4 y \)
\( 16 y^{2}-20 y+4=0^{\prime} \)
\( 4 y^{2}-5 y+1=0 \)
\( 4 y^{2}-4 y-y+1=0 \)
\( 4 y(y-1)-1(y-1)=0 y=1 \) \(\text{or} \ y=\frac{ 1 }{ 4 } \ \text {Corresponding values of}\) \( x \) are, \( x \) \( =2 \) or \( x=-1 \) Therefore,
Coordinates of point A are \( \left(-1, \frac{1}{4}\right) \)
Coordinates of point B are \( (2,1) \).
Now, draw AL and BM perpendicular to x axis.
We can see that,
Area \( \mathrm{OBCA}= \) \( \text {Area of line - Area of Parabola} \ldots(1)\)
\(=\int_{-1}^{2}\left(\frac{x+2}{4}-\frac{x^{2}}{4}\right) d x\)
\(=\frac{1}{4}\left[\frac{x^{2}}{2}+2 x-\frac{x^{3}}{12}\right]_{-1}^{2}\)
\(=\left(\frac{4}{8}+\frac{2}{2}-\frac{8}{12}\right)-\left(\frac{1}{8}-\frac{1}{2}+\frac{1}{12}\right)\)
\(=\frac{9}{8} \text { sq. units }\)
Hence, the area bounded by the \( x^{2}=4 y \) and the line \( x=4 y-2 \) is \( \frac{9}{8} \) square units.

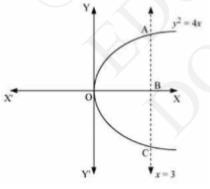
It is given that the region bounded by parabola, \( y 2=4 x \) and the line \( x= \) 3 .
From the figure we can see that the required is OACO.
We can observe that the area OACO is symmetrical about x -axis.
Thus, Area of \( \mathrm{OACO}=2 \) (Area of OAB )
So, Area \( \mathrm{OACO}=2\left[\int_{0}^{3} y d x\right]=2 \int_{0}^{3} 2 \sqrt{x} d x \)
\(=4\left[\frac{x^{\frac{3}{2}}}{\frac{3}{2}}\right]_{0}^{3}=\frac{8}{3}(3)^{\frac{3}{2}}=8 \sqrt{3}\)
Therefore, the required area is \( 8 \sqrt{3} \) square units

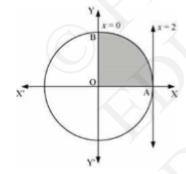
The area bounded by the circle and the lines, \( x=0 \) and \( x=2 \), in the first quadrant is shown by shaded region in above figure.
Area of \( \mathrm{OAB}=\int_{0}^{2} y d x=\int_{0}^{2} \sqrt{4-x^{2}} d x \)
\(=\left[\frac{x}{2} \sqrt{4-x^{2}}+\frac{4}{2} \sin ^{-1} \frac{x}{2}\right]_{0}^{2}\)
\(=2\left(\frac{\pi}{2}\right)=\pi\)

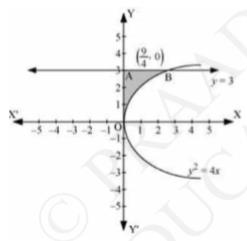
The area bounded by the curve \( y^{2}=4 x, y \)-axis and the line \( y=3 \) is shown by shaded region in above figure.
Thus, Area \( \mathrm{OAB}=\int_{0}^{3} x d y=\int_{0}^{3} \frac{y^{2}}{4} d y \)
\(=\frac{1}{4}\left[\frac{y^{3}}{3}\right]_{0}^{-2}\)
\(=\frac{1}{12}(27)=\frac{9}{4}\)
Therefore, required area is \( =\frac{9}{4} \) square units