Ex 8.2 class 12 maths ncert solutions | class 12 maths exercise 8.2 | class 12 maths ncert solutions chapter 8 exercise 8.2 | exercise 8.2 class 12 maths ncert solutions | class 12 maths chapter 8 ncert solutions | class 12 chapter 8 maths ncert solutions | applications of integrals class 12
Exercise 8.2 Class 12 Maths NCERT Solutions is a significant section of the chapter on Applications of Integrals Class 12, where students learn to find areas enclosed between curves. The Class 12 Maths Exercise 8.2 focuses on solving problems using definite integrals to calculate the area between two given curves, which is a practical application in calculus. The Class 12 Maths NCERT Solutions Chapter 8 Exercise 8.2 provides detailed and accurate methods to solve such problems, making it easier for students to grasp the underlying concepts. These Exercise 8.2 Class 12 Maths NCERT Solutions are designed in accordance with the latest CBSE syllabus and are highly useful for board exam preparation.

class 12 maths chapter 8 ncert solutions || class 12 maths exercise 8.2 || class 12 maths ncert solutions chapter 8 exercise 8.2 || class 12 chapter 8 maths ncert solutions || ex 8.2 class 12 maths ncert solutions || applications of integrals class 12 || exercise 8.2 class 12 maths ncert solutions
Exercise 8.2
1. Find the area of the circle \( 4 x^{2}+4 y^{2}=9 \) which is interior to the parabola \( x^{2}=4 y \).
Answer
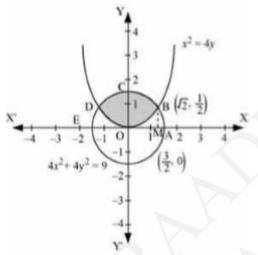
It is given that of circle, \( 4 x^{2}+4 y^{2}=9 \) and parabola \( x^{2}=4 y \).
On solving the above two equations, we get the point of intersection \( B\left(\sqrt{2} \cdot \frac{1}{2}\right) \) and \( D\left(-\sqrt{2} \cdot \frac{1}{2}\right) \)
We can see that the required area is symmetrical about \( y \) axis.
Thus, Area \( \mathrm{OBCDO}=2 \times \) Area OBCO
Let us draw BM perpendicular to OA.
\( \Rightarrow \) The coordinates of M are \( (\sqrt{2}, 0) \).
Then, Area \( \mathrm{OBCO}= \) Area \( \mathrm{OABCO}- \) Area OABO
\(=\int_{0}^{\sqrt{2}} \sqrt{\frac{\left(9-4 x^{2}\right)}{4}} d x-\int_{0}^{\sqrt{2}} \sqrt{\frac{x^{2}}{4}} d x\)
\(=\frac{1}{2} \int_{0}^{\sqrt{2}} \sqrt{\left(9-4 x^{2}\right)} d x-\frac{1}{4} \int_{0}^{\sqrt{2}} x^{2} d x\)
\(=\frac{1}{4}\left[x \sqrt{\left(9-4 x^{2}\right)}+\frac{9}{2} \sin ^{-1} \frac{2 \sqrt{2}}{3}\right]-\frac{1}{12}(\sqrt{2})^{3}\)
\(=\frac{\sqrt{2}}{4}+\frac{9}{8} \sin ^{-1} \frac{2 \sqrt{3}}{3}-\frac{\sqrt{2}}{6}\)
\(=\frac{\sqrt{2}}{12}+\frac{9}{8} \sin ^{-1} \frac{2 \sqrt{3}}{3}\)
\(=\frac{1}{2}\left(\frac{\sqrt{2}}{6}+\frac{9}{4} \sin ^{-1} \frac{2 \sqrt{3}}{3}\right)\)
\( \text{Therefore, the required area OBCDO is} \left(2 \times \frac{1}{2}\left[\frac{\sqrt{2}}{6}+\frac{9}{4} \sin ^{-1} \frac{2 \sqrt{3}}{3}\right]\right)\)
\(=\left[\frac{\sqrt{2}}{6}+\frac{9}{4} \sin ^{-1} \frac{2 \sqrt{3}}{3}\right] \) units
2. Find the area bounded by curves \( (x-1)^{2}+y^{2}=1 \) and \( x^{2}+ \) \( y^{2}=1 \).
Answer
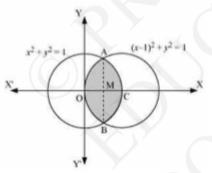
It is given that area of circle, \( (x-1)^{2}+y^{2}=1 \) and \( x^{2}+y^{2}=1 \).
On solving the above two equations, we get the point of intersection
\( A\left(\frac{1}{2}, \frac{\sqrt{3}}{2}\right) \) and \( B\left(\frac{1}{2},-\frac{\sqrt{3}}{2}\right) \)
We can see that the required area is symmetrical about x axis.
Thus, Area \( \mathrm{OBCAO}=2 \times \) Area OCAO
Let us draw AM perpendicular to OC.
\( \Rightarrow \) The coordinates of M are \( \left(\frac{1}{2}, 0\right) \).
Then, Area OCAO \( = \) Area OMAO + Area MCAM
\(=\int_{0}^{\frac{1}{2}} \sqrt{1-(x-1)^{2}} d x+\int_{\frac{1}{2}}^{1} \sqrt{1-x^{2}} d x\)
\(=\left[\frac{x-1}{2} \sqrt{1-(x-1)^{2}}+\frac{1}{2} \sin ^{-1}(x-1)\right]_{0}^{\frac{1}{2}}+\left[\frac{x}{2} \sqrt{1-x^{2}}+\frac{1}{2} \sin ^{-1} x\right]_{0}^{\frac{1}{2}}\)
\(=\left[-\frac{1}{4} \sqrt{1-\left(-\frac{1}{2}\right)^{2}}+\frac{1}{2} \sin ^{-1}\left(\frac{1}{2}-1\right)-\frac{1}{2} \sin ^{-1}(1)\right]\)
\(\quad+\left[\frac{1}{2} \sin ^{-1}(1)-\frac{1}{4} \sqrt{1-\left(\frac{1}{2}\right)^{2}}-\frac{1}{2} \sin ^{-1}\left(\frac{1}{2}\right)\right]\)
\(=\left[-\frac{\sqrt{3}}{8}+\frac{1}{2}\left(-\frac{\pi}{6}\right)-\frac{1}{2}\left(-\frac{\pi}{2}\right)\right]+\left[\frac{1}{2}\left(\frac{\pi}{2}\right)-\frac{\sqrt{3}}{8}+\frac{1}{2}\left(\frac{\pi}{6}\right)\right]\)
\(=\left[-\frac{\sqrt{3}}{4}-\frac{\pi}{12}+\frac{\pi}{4}+\frac{\pi}{4}-\frac{\pi}{12}\right]\)
\(=\left[-\frac{\sqrt{3}}{4}-\frac{\pi}{6}+\frac{\pi}{2}\right]\)
\(=\left[\frac{\pi}{3}-\frac{\sqrt{3}}{4}\right]\)
\( \text {Therefore, the required area } \mathrm{OBCAO}=2\left[\frac{\pi}{3}-\frac{\sqrt{3}}{4}\right]=\left[\frac{2 \pi}{3}-\frac{\sqrt{3}}{2}\right] \) units
3. Find the area of the region bounded by the curves \( y=x^{2}+2 \), \( y=x, x=0 \) and \( x=3 \).
Answer
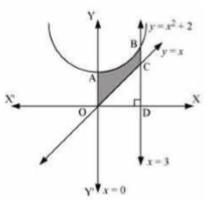
\( \text {It is given that equation of curve are} \ y=x^{2}+2, y=x, x=0 \) and \( x=3 \). The required area is shown by shaded region.
\(=\int_{0}^{3}\left(x^{2}+2\right) d x-\int_{0}^{3} x d x\)
\(=\left[\frac{x^{3}}{3}+2 x\right]_{0}^{3}-\left[\frac{x^{2}}{2}\right]_{0}^{3}\)
\(=[9-6]-\left[\frac{9}{2}\right]\)
\(=15-\left[\frac{9}{2}\right]\)
\(=\frac{21}{2} \text { units }\)
class 12 maths chapter 8 ncert solutions || class 12 maths exercise 8.2 || class 12 maths ncert solutions chapter 8 exercise 8.2 || class 12 chapter 8 maths ncert solutions || ex 8.2 class 12 maths ncert solutions || applications of integrals class 12 || exercise 8.2 class 12 maths ncert solutions
4. Using integration find the area of region bounded by the triangle whose vertices are \( (-1,0),(1,3) \) and \( (3,2) \).
Answer
BL and CM are drawn perpendicular to \( x- \) axis.
We can see that from the figure that,
\( \operatorname{Area}(\triangle \mathrm{ACB})=\operatorname{Area}(\mathrm{ALBA})+\operatorname{Area}(\mathrm{BLMCA})-\operatorname{Area}(\mathrm{AMCA}) \ldots(1) \)
Now, equation of line segment \( A B \) is
\(y-0=\frac{3-0}{1+1}(x+1)\)
\(\Rightarrow y=\frac{3}{2}(x+1)\)
\( \text {Thus, Area}( \) ALBA \( )=\int_{-1}^{1} \frac{3}{2}(x+1) d x=\frac{3}{2}\left[\frac{x^{2}}{2}+x\right]_{-1}^{1} \)
\(=\frac{3}{2}\left[\frac{1}{2}+1-\frac{1}{2}+1\right]=3 \text { units }\)
Now, equation of line segment BC is
\(y-3=\frac{2-3}{3-1}(x-1)\)
\(\Rightarrow y=\frac{1}{2}(-x+7)\)
\( \text{Thus, Area} (\mathrm{BLMCB})=\int_{1}^{3} \frac{1}{2}(-x+7) d x=\frac{1}{2}\left[-\frac{x^{2}}{2}+7 x\right]_{1}^{3} \) \( =\frac{1}{2}\left[-\frac{9}{2}+21+\frac{1}{2}-7\right]=5 \) units
Now, equation of line segment \( A C \) is
\(y-0=\frac{2-0}{3+1}(x+1)\)
\(\Rightarrow y=\frac{1}{2}(x+1)\)
Thus, Area \( (\mathrm{AMCA})=\int_{-1}^{3} \frac{1}{2}(x+1) d x=\frac{1}{2}\left[\frac{x^{2}}{2}+x\right]_{-1}^{3} \)
\(=\frac{1}{2}\left[\frac{9}{2}+3-\frac{1}{2}+1\right]=4 \text { units }\)
Now putting all these values in equation (1), we get, \( \operatorname{Area}(\triangle \mathrm{ABC})=(3+5-4)=4 \) units.
5. Using integration find the area of the triangular region whose sides have the equations \( y=2 x+1, y=3 x+1 \) and \( x=4 \).
Answer
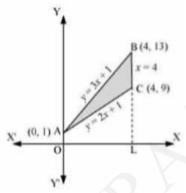
The equation of the sides of the triangle are \( y=2 x+1, y=3 x+1 \) and \( x \) \( =4 \).
So, solving above equations, we get the vertices of triangle are \( \mathrm{A}(0,1) \), B \( (4,13) \) and \( \mathrm{c}(4,9) \).
We can see that Area \( (\triangle \mathrm{ACB})= \) Area \( (\mathrm{OLBAO})- \) Area \( (\mathrm{OLCAO}) \)
\(=\int_{0}^{4}(3 x+1) d x-\int_{0}^{4}(2 x+1) d x\)
\(=\left[\frac{3 x^{2}}{2}+x\right]_{0}^{4}-\left[\frac{2 x^{2}}{2}+x\right]_{0}^{4}\)
\(=(24+4)-(16+4)\)
\(=28-20\)
\(=8 \text { units. }\)
Therefore, the required are is 8 units.
6. Smaller area enclosed by the circle \( x^{2}+y^{2}=4 \) and the line \( x \) \( +y=2 \) is
A. \( 2(\pi-2) \) B. \( \pi-2 \) C. \( 2 \pi-1 \) D. \( 2(\pi+2) \)
A. \( 2(\pi-2) \) B. \( \pi-2 \) C. \( 2 \pi-1 \) D. \( 2(\pi+2) \)
Answer
The smaller area enclosed by the circle \( x^{2}+y^{2}=4 \) and the line \( x+y=2 \) is shown by shaded region.
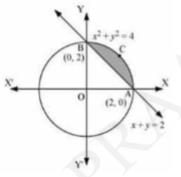
We can see that
Area \( \mathrm{ACBA}=\operatorname{Area}(\mathrm{OACBO})-\operatorname{Area}(\triangle \mathrm{OAB}) \)
\(=\int_{0}^{2} \sqrt{4-x^{2}} d x-\int_{0}^{2}(2-x) d x\)
\(=\left[\frac{x}{2} \sqrt{4-x^{2}}+\frac{4}{2} \sin ^{-1} \frac{x}{2}\right]_{0}^{2}-\left[2 x-\frac{x^{2}}{2}\right]_{0}^{2}\)
\(=\left[2 \cdot \frac{\pi}{2}\right]-[4-2]\)
\(=(\pi-2) \text { units }\)
7. Area lying between the curves \( y^{2}=4 x \) and \( y=2 x \) is
A. \( \frac{2}{3} \) B. \( \frac{1}{3} \) C. \( \frac{1}{4} \) D. \( \frac{3}{4} \)
A. \( \frac{2}{3} \) B. \( \frac{1}{3} \) C. \( \frac{1}{4} \) D. \( \frac{3}{4} \)
Answer
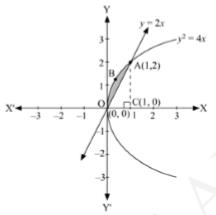
The points of intersection of these curves are \( O(0,0) \) and \( A(1,2) \)
Now, we draw a perpendicular to x -axis such that the coordinates of C are \( (1,0) \).
Thus, Area \( \mathrm{OBAO}=\operatorname{Area}(\mathrm{OCABO})-\operatorname{Area}(\triangle \mathrm{OCA}) \)
\(=\int_{0}^{1} 2 \sqrt{x} d x-\int_{0}^{1}(2 x) d x\)
\(=2\left[\frac{x^{\frac{3}{2}}}{\frac{3}{2}}\right]_{0}^{1}-2\left[\frac{x^{2}}{2}\right]_{0}^{1}\)
\(=\frac{4}{3}-1\)
\(=\frac{1}{3} \text { units square }\)
