Ex 9.3 class 12 maths ncert solutions | class 12 maths exercise 9.3 | class 12 maths ncert solutions chapter 9 exercise 9.3 | exercise 9.3 class 12 maths ncert solutions | chapter 9 class 12 maths ncert solutions | differential equations class 12 ncert solutions
The Class 12 Maths NCERT Solutions Chapter 9 Exercise 9.3 offers a simple and clear approach to solving problems related to differential equations. This exercise helps students understand how to recognize and work through real-world mathematical relationships step by step. The exercise 9.3 class 12 maths NCERT solutions are designed to build problem-solving skills and improve confidence for board exams. Whether you’re revising or learning the concept for the first time, the class 12 maths exercise 9.3 gives you a solid grasp of the topic in a structured way.

differential equations class 12 ncert solutions || class 12 maths ncert solutions chapter 9 exercise 9.3 || ex 9.3 class 12 maths ncert solutions || exercise 9.3 class 12 maths ncert solutions || chapter 9 class 12 maths ncert solutions || class 12 maths exercise 9.3
EXERCISE 9.3
1. In each of the question, form a differential equation representing the given family of curves by eliminating arbitrary constants a and b.
\(\frac{x}{a}+\frac{y}{b}=1\)
\(\frac{x}{a}+\frac{y}{b}=1\)
Answer
The given equation is \( \frac{x}{a}+\frac{y}{b}=1 \)
Now, differentiating both sides w.r.t \(x \), we get,
\(\frac{1}{a}+\frac{1}{b} \frac{d y}{d x}=0\)
\(\Rightarrow \frac{1}{a}+\frac{1}{b} y^{\prime}=0\)
Now, again differentiating both sides, we get,
\(0+\frac{1}{b} y^{\prime \prime}=0\)
\(\Rightarrow \frac{1}{b} y^{\prime \prime}=0\)
\(\Rightarrow y^{\prime \prime}=0\)
Therefore, the required differential equation is \( y^{\prime \prime}=0 \).
2. In each of the question, form a differential equation representing the given family of curves by eliminating arbitrary constants a and b.
\(y^{2}=a\left(b^{2}-x^{2}\right)\)
\(y^{2}=a\left(b^{2}-x^{2}\right)\)
Answer
The given equation is \( y^{2}=a\left(b^{2}-x^{2}\right) \)
Now, differentiating both sides w.r.t \( x \), we get
\(2 y \frac{d y}{d x}=a(-2 x)\)
\(\Rightarrow 2 \mathrm{yy}^{\prime}=-2 \mathrm{a}x\)
\(\Rightarrow \mathrm{yy}^{\prime}=-\mathrm{a}x\quad \ldots\ldots\text{(1)}\)
Now, again differentiating both sides, we get,
\(y^{\prime} \cdot y^{\prime}+y y^{\prime \prime}=-a\)
\(\Rightarrow\left(y^{\prime}\right)^{2}+y y^{\prime \prime}=-a\quad \ldots\ldots\text{(2)}\)
Now, dividing equation (2) by (1), we get,
\(\frac{\left(y^{\prime}\right)^{2}+y y^{\prime \prime}}{y y \prime}=\frac{-a}{a x}\)
\(\Rightarrow x y y^{\prime \prime}+x\left(y^{\prime}\right)^{2}-\mathrm{yy}{ }^{\prime \prime}=0\)
Therefore, the required differential equation is \( x y y^{\prime \prime}+x\left(y^{\prime}\right)^{2}-\mathrm{yy}^{\prime \prime}=0 \).
3. In each of the question, form a differential equation representing the given family of curves by eliminating arbitrary constants a and b.
\(y=a e^{3 x}+b e^{-2 x}\)
\(y=a e^{3 x}+b e^{-2 x}\)
Answer
It is given that \( y=a e^{3 x}+b e^{-2 x}\quad \ldots\ldots\text{(1)}\)
Now, differentiating both side we get,
\(y^{\prime}=3 a e^{3 x}-2 b e^{-2 x}\quad \ldots\ldots\text{(2)}\)
Now, again differentiating both sides, we get,
\(y^{\prime \prime}=9 a e^{3 x}+4 b e^{-2 x}\quad \ldots\ldots\text{(3)}\)
Now, let us multiply equation (1) with 2 and then adding it to equation (2), we get,
\(\left(2 \mathrm{ae}^{3 x}+2 \mathrm{be}^{-2 x}\right)+\left(3 \mathrm{ae}^{3 x}-2 \mathrm{be}^{-2 x}\right)=2 \mathrm{y}-\mathrm{y}^{\prime}\)
\(\Rightarrow 5 \mathrm{ae}^{3 x}=2 \mathrm{y}+\mathrm{y}\)
\(\Rightarrow a e^{3 x}=\frac{2 y+y^{\prime}}{5}\)
Now, let us multiply equation (1) with 3 and subtracting equation (2), we get
\(\left(3 \mathrm{ae}^{3 x}+3 \mathrm{be}^{-2 x}\right)-\left(3 \mathrm{ae}^{3 x}-2 \mathrm{be}^{-2 x}\right)=3 \mathrm{y}-\mathrm{y}^{\prime}\)
\(\Rightarrow 5 \mathrm{be}^{-2 x}=3 \mathrm{y}-\mathrm{y}^{\prime}\)
\(\Rightarrow b e^{-2 x}=\frac{3 y+y^{\prime}}{5}\)
\(y^{\prime \prime}=9 \cdot \frac{2 y+y^{\prime}}{5}+4 \frac{2 y+y^{\prime}}{5}\)
\(\Rightarrow y^{\prime \prime}=\frac{18 y+9 y^{\prime}}{5}+\frac{12 y-4 y^{\prime}}{5}\)
\(\Rightarrow y^{\prime \prime}=\frac{30 y+5 y^{\prime}}{5}\)
\(\Rightarrow y^{\prime \prime}=6 \mathrm{y}+\mathrm{y}^{\prime}\)
\(\Rightarrow y^{\prime \prime}-y^{\prime}-6 \mathrm{y}=0\)
Therefore, the required differential equation is \( y^{\prime \prime}-y^{\prime}-6 y=0 \).
4. In each of the question, form a differential equation representing the given family of curves by eliminating arbitrary constants a and b.
\(y=e^{2 x}(a+b x)\)
\(y=e^{2 x}(a+b x)\)
Answer
It is given \( y=e^{2 x}(a+b x) \quad \ldots\ldots\text{(1)}\)
Now, differentiating both side w.r.t. \( x \), we get,
\(y^{\prime}=2 e^{2 x}(a+b x)+e^{2 x} \cdot b \quad \ldots\ldots\text{(2)}\)
Now, let us multiply equation (1) with 2 and then subtracting it to equation (2), we get,
\(y^{\prime}-2 y=e^{2 x}(2 a+2 b x+b)-e^{2 x}(2 a+2 b x)\)
\(\Rightarrow y^{\prime}-2 y=b e^{2 x}\quad \ldots\ldots\text{(3)}\)
Now, again differentiating both sides w.r.t. \(x\), we get,
\(y^{\prime \prime}-2 y^{\prime}=2 b e^{2 x}\quad \ldots\ldots\text{(4)}\)
Dividing equation (4) by equation (3), we get,
\(\frac{y^{\prime \prime}+2 y^{\prime}}{y^{\prime}-2 y}=2\)
\(\Rightarrow y^{\prime \prime}-2 y^{\prime}=2 y^{\prime}-4 y\)
\(\Rightarrow y^{\prime \prime}-4 y^{\prime}-4 y=0\)
Therefore, the required differential equation is \( y^{\prime \prime}-4 y^{\prime}-4 y=0 \).
differential equations class 12 ncert solutions || class 12 maths ncert solutions chapter 9 exercise 9.3 || ex 9.3 class 12 maths ncert solutions || exercise 9.3 class 12 maths ncert solutions || chapter 9 class 12 maths ncert solutions || class 12 maths exercise 9.3
5. In each of the question, form a differential equation representing the given family of curves by eliminating arbitrary constants \( a \) and \( b \).
\(y=e^{x}(a \cos x+b \sin x)\)
\(y=e^{x}(a \cos x+b \sin x)\)
Answer
It is given that \( y=e^{x}(a \cos x+b \sin x)\quad \ldots\ldots\text{(1)} \)
Now, differentiating both w.r.t. \( x \), we get,
\(y^{\prime}=e^{x}(a \cos x+b \sin x)+e^{x}(-a \sin x+b \cos x)\)
\(\left.\Rightarrow y^{\prime}=e^{x}[(a+b) \cos x-(a-b) \sin x)\right]\quad \ldots\ldots\text{(2)}\)
Again, differentiating both sides w.r.t. \(x \), we get,
\(\left.\left.y^{\prime \prime}=e^{x}[(a+b) \cos x-(a-b) \sin x)\right]+e^{x}[-(a+b) \sin x-(a-b) \cos x)\right]\)
\(\Rightarrow y^{\prime \prime}=e^{x}[2 b \cos x-2 a \sin x]\)
\(\Rightarrow y^{\prime \prime}=2 e^{x}(b \cos x-a \sin x)\quad \ldots\ldots\text{(3)}\)
Adding equation (1) and (3), we get,
\(y+\frac{y \prime \prime}{2}=e^{x}[(a+b)] \cos x-(a-b) \sin x\)
\(y+\frac{y \prime \prime}{2}=y^{\prime}\)
\(\Rightarrow 2 y+y^{\prime \prime}=2 y^{\prime}\)
Therefore, the required differential equation is \( 2 y+y^{\prime \prime}=2 y^{\prime}=0 \).
6. Form the differential equation of the family of circles touching the \( y \)-axis at origin.
Answer
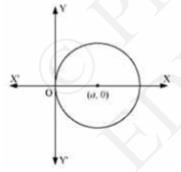
The center of the circle touching the \(y\) - axis at orgin lies on the \( x \) - axis.
Let \( (a, 0) \) be the centre of the circle.
Thus, it touches the \( y \) - axis at orgin, its radius is a.
Now, the equation of the circle with centre \( (a, 0) \) and radius (a) is
\((x-a)^{2}-y^{2}=a^{2}\)
\(\Rightarrow x^{2}+y^{2}=2 a x\)
Now, differentiating both sides w.r.t. \(x \), we get,
\(2 x+2 \mathrm{yy}^{\prime}=2 \mathrm{a}\)
\(\Rightarrow x+\mathrm{yy}^{\prime}=\mathrm{a}\)
Now, on substituting the value of a in the equation, we get,
\(x^{2}+y^{2}=2\left(x+y y^{\prime}\right) x\)
\(\Rightarrow 2 x y y^{\prime}+x^{2}=y^{2} \)
Therefore, the required differential equation is \( 2 x y y^{\prime}+x^{2}=y^{2} \).
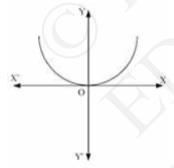
7. Form the differential equation of the family of parabolas having vertex at origin and axis along positive \( y \)-axis.
Answer
We know that the equation of the parabola having the vertex at origin and the axis along the positive \( y \) - axis is
\( x^{2}=4 a y\quad \ldots\ldots\text{(1)} \)
Now, differentiating equation (1) w.r.t. \(x\), we get,
\(2 x=4 a y\quad \ldots\ldots\text{(2)}\)
On dividing equation (2) by equation (1), we get,
\(\frac{2 x}{x^{2}}=\frac{4 a y \prime}{4 a y}\)
\(\Rightarrow \frac{2}{x}=\frac{y^{\prime}}{y}\)
\(\Rightarrow x y^{\prime}=2 y\)
\(\Rightarrow x y^{\prime}-2 y=0\)
Therefore, the required differential equation is \( x y^{\prime}-2 y=0 \).
differential equations class 12 ncert solutions || class 12 maths ncert solutions chapter 9 exercise 9.3 || ex 9.3 class 12 maths ncert solutions || exercise 9.3 class 12 maths ncert solutions || chapter 9 class 12 maths ncert solutions || class 12 maths exercise 9.3
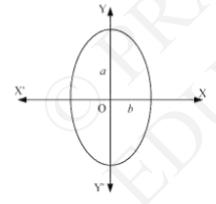
8. Form the differential equation of the family of ellipses having foci on \( y \)-axis and centre at origin.
Answer
We know that the equation of the family of ellipses having foci on \( y \) - axis and the centre at origin is
\( \frac{x^{2}}{b^{2}}+\frac{y^{2}}{a^{2}}=1 \quad \ldots\ldots\text{(1)}\)
Now, differentiating equation (1) w.r.t. \(x\), we get,
\(\frac{2 x}{b^{2}}+\frac{2 y y^{\prime}}{a^{2}}=0\)
\(\Rightarrow \frac{x}{b^{2}}+\frac{y y^{\prime}}{a^{2}}=0\quad \ldots\ldots\text{(2)}\)
Now, again differentiating w.r.t. \(x \), we get,
\(\frac{1}{b^{2}}+\frac{y^{\prime} y^{\prime}+y^{\prime \prime}}{a^{2}}=0\)
\(\Rightarrow \frac{1}{b^{2}}+\frac{1}{a^{2}}\left(y^{\prime 2}+y y^{\prime \prime}\right)=0\)
\(\Rightarrow \frac{1}{b^{2}}=-\frac{1}{a^{2}}\left(y^{\prime 2}+y y^{\prime \prime}\right)=0\)
Let us substitute the value in eq. (2), we get,
\( x\left[-\frac{1}{a^{2}}\left(y^{\prime 2}+y^{\prime \prime}\right)\right]+\frac{y y^{\prime}}{a^{2}}=0\)
\(\Rightarrow-{x}\left(y^{\prime}\right)^{2}-x y y^{\prime \prime}+{yy}^{\prime}=0\)
\(\Rightarrow {xyy} '+{x}\left({y}^{\prime}\right)^{2}-{yy} y^{\prime}=0 \)
Therefore, the required differential equation is \( xyy^{\prime \prime}+x\left(y^{\prime}\right)^{2}-yy^{\prime}=0 \).
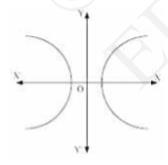
9. Form the differential equation of the family of hyperbolas having foci on \(x \)-axis and centre at origin.
Answer
We know that the equation of the family of hyperbolas having foci on \( x \)-axis and the centre at origin is
\( \frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\quad \ldots\ldots\text{(1)} \)
Now, differentiating equation (1) w.r.t. \(x\), we get,
\(\frac{2 x}{a^{2}}-\frac{2 y y^{\prime}}{b^{2}}=0\)
\(\Rightarrow \frac{x}{a^{2}}-\frac{y y^{\prime}}{b^{2}}=0\quad \ldots\ldots\text{(2)}\)
Now, again differentiating w.r.t. \(x \), we get,
\(\frac{1}{a^{2}}-\frac{y^{\prime} y^{\prime}+y y^{\prime \prime}}{b^{2}}=0\)
\(\Rightarrow \frac{1}{a^{2}}-\frac{1}{b^{2}}\left(y^{\prime 2}+y y^{\prime \prime}\right)=0\)
\(\Rightarrow \frac{1}{a^{2}}=\frac{1}{b^{2}}\left(y^{\prime 2}+y^{\prime \prime}\right)\)
Let us substitute the value in eq. (2), we get,
\(\frac{x}{b^{2}}\left(\left(y^{\prime 2}+y y^{\prime \prime}\right)\right)-\frac{y y^{\prime}}{b^{2}}=0\)
\(\Rightarrow x\left(y^{\prime}\right)^{2}+x y y^{\prime \prime}-{yy} y^{\prime}=0\)
\(\Rightarrow {xyy}{ }^{\prime \prime}+x\left({y}^{\prime}\right)^{2}-{yy}=0\)
Therefore, the required differential equation is \( x y y^{\prime \prime}+x\left(y^{\prime}\right)^{2}-y y^{\prime}=0 \).
10. Form the differential equation of the family of circles having centre on \( y \)-axis and radius 3 units.
Answer
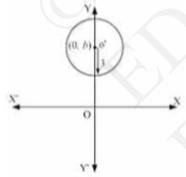
Let the centre of the circle on \( y \) - axis be \( (0, b) \).
We know that the differential equation of the family of circles with centre at \( (0, b) \) and radius 3 is: \( x^{2}+(y-b)^{2}=3^{2} \)
\(\Rightarrow x^{2}+(y-b)^{2}=9\quad \ldots\ldots\text{(1)}\)
Now, differentiating both sides w.r.t. \(x \), we get,
\(2 x+2(y-b) \cdot y^{\prime}=0\)
\(\Rightarrow(y-b) \cdot y^{\prime}=x\)
\(\Rightarrow y-b=\frac{-x}{y^{\prime}}\)
Thus, substituting the value of \( (y-b) \) in equation (1), we get,
\(x^{2}+\left(\frac{-x}{y^{\prime}}\right)^{2}=9\)
\(\Rightarrow x^{2}\left[1+\frac{1}{\left(y^{\prime}\right)^{2}}\right]=9\)
\(\Rightarrow x^{2}\left(\left(y^{\prime}\right)^{2}+1\right)=9\left(y^{\prime}\right)^{2}\)
\(\Rightarrow\left(x^{2}-9\right)\left(y^{\prime}\right)^{2}+x^{2}=0\)
Therefore, the required differential equation is \( \left(x^{2}-9\right)\left(y^{\prime}\right)^{2}+x^{2}=0 \)
11. Which of the following differential equations has \( \mathrm{y}=\mathrm{c}_{1} \mathrm{e}^{x} +\mathrm{c}_{2} \mathrm{e}^{-x} \) as the general solution ?
A. \( \frac{d^{2} y}{d x^{2}}+y=0 \) B. \( \frac{d^{2} y}{d x^{2}}-y=0 \) C. \( \frac{d^{2} y}{d x^{2}}+1=0 \) D. \( \frac{d^{2} y}{d x^{2}}-1=0 \)
A. \( \frac{d^{2} y}{d x^{2}}+y=0 \) B. \( \frac{d^{2} y}{d x^{2}}-y=0 \) C. \( \frac{d^{2} y}{d x^{2}}+1=0 \) D. \( \frac{d^{2} y}{d x^{2}}-1=0 \)
Answer
It is given that \( y=c_{1} e^{x}+c_{2} e^{-x} \)
Now, differentiating both sides w.r.t. \(x \), we get,
\(\frac{d y}{d x}=\mathrm{c}_{1} \mathrm{e}^{x}+\mathrm{c}_{2} \mathrm{e}^{-x}\)
Again, differentiating both sides w.r.t. \(x\), we get,
\(\frac{d^{2} y}{d x^{2}}=\mathrm{c}_{1} \mathrm{e}^{x}+\mathrm{c}_{2} \mathrm{e}^{-x}\)
\(\Rightarrow \frac{d^{2} y}{d x^{2}}=y\)
\(\Rightarrow \frac{d^{2} y}{d x^{2}}-y=0\)
Therefore, the required differential equation is \( \frac{d^{2} y}{d x^{2}}-y=0 \)
12. Which of the following differential equations has \( \mathrm{y}=x \) as one of its particular solution?
A. \( \frac{d^{2} y}{d x^{2}}-x^{2} \frac{d y}{d x}+x y=x \)
B. \( \frac{d^{2} y}{d x^{2}}+x \frac{d y}{d x}+x y=x \)
C. \( \frac{d^{2} y}{d x^{2}}-x^{2} \frac{d y}{d x}+x y=x \)
D. \( \frac{d^{2} y}{d x^{2}}+x \frac{d y}{d x}+x y=x \)
A. \( \frac{d^{2} y}{d x^{2}}-x^{2} \frac{d y}{d x}+x y=x \)
B. \( \frac{d^{2} y}{d x^{2}}+x \frac{d y}{d x}+x y=x \)
C. \( \frac{d^{2} y}{d x^{2}}-x^{2} \frac{d y}{d x}+x y=x \)
D. \( \frac{d^{2} y}{d x^{2}}+x \frac{d y}{d x}+x y=x \)
Answer
It is given that that \( y=x \)
Now, differentiating both sides w.r.t. \( x \), we get,
\( \frac{d y}{d x}=1 \)
Again, differentiating both sides w.r.t. \(x\), we get,
\(\frac{d^{2} y}{d x^{2}}=0\)
Now, substitute the value of \( \frac{d y}{d x} \) and \( \frac{d^{2} y}{d x^{2}} \) in the given options, we will see that the differential equation in option (C) is correct.
\(\frac{d^{2} y}{d x^{2}}-x^{2} \frac{d y}{d x}+x y=0-x^{2} \cdot 1+x \cdot x\)
\(=-x^{2}+x^{2}\)
\(=0\)
