NCERT Solutions for Class 10 Maths Chapter 10: Circles CBSE Class 10 Maths Chapter 10 Circles solutions Ex 10.2
Discover the complete NCERT Solutions for Class 10 Maths Chapter 10 Circles solutions (English Medium), with step-by-step explanations for Exercise 10.1 and Exercise 10.2. This resource ensures a thorough understanding of Circles, helping Class 10 Maths students excel in their exams. If you have any queries regarding the NCERT Solutions for Class 10 Maths Chapter 10 Circles solutions Ex 10.2, drop a comment below, and we’ll assist you at the earliest.

CBSE Class 10 maths chapter 10 Ex 10.2 || NCERT Solutions for Class
10 Maths Chapter 10 Exercise 10.2
Exercise 10.2
CBSE Class 10 maths chapter 10 Ex 10.2 || NCERT Solutions for Class 10 Maths Chapter 10 Exercise 10.2
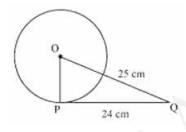
Let \(\mathrm{Q} \) be the centre of the circle.
Given that,
\( \mathrm{OQ}=25 \mathrm{~cm} \) and \( \mathrm{PQ}=24 \mathrm{~cm} \)
As the radius is perpendicular to the tangent at the point of contact, Therefore, \( \mathrm{OP} \perp \mathrm{PQ} \)
Applying Pythagoras theorem in \( \triangle \mathrm{OPQ} \), we obtain
\(\mathrm{OP}^{2}+\mathrm{PQ}^{2}=\mathrm{OQ}^{2}\)
\(\mathrm{OP}^{2}+24^{2}=25^{2}\)
\(\mathrm{OP}^{2}=625-576\)
\(\mathrm{OP}^{2}=49\)
\(\mathrm{OP}=\sqrt{49}=7\)
Therefore, the radius of the circle is \(7\) cm .
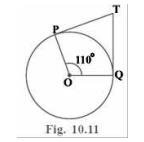
Given: TP and TQ are tangents.
Therefore, radius drawn to these tangents from centre of the circle will be perpendicular to the tangents.
Thus, \( \mathrm{OP} \perp \mathrm{TP} \) and \( \mathrm{OQ} \perp \mathrm{TQ} \)
And therefore,
\(\angle \mathrm{OPT}=90^{\circ}\)
\(\angle \mathrm{OQT}=90^{\circ}\)
In quadrilateral \(\mathrm{POQT}\) ,
Sum of all interior angles \( =360^{\circ} \)
\(\angle \mathrm{OPT}+\angle \mathrm{POQ}+\angle \mathrm{OQT}+\angle \mathrm{PTQ}=360^{\circ}\)
\(90^{\circ}+110^{\circ}+90^{\circ}+\angle \mathrm{PTQ}=360^{\circ}\)
\(\angle \mathrm{PTQ}=\mathbf{7 0}^{\circ}\)
Therefore, radius drawn to these tangents from centre of the circle will be perpendicular to the tangents.
Thus, \( \mathrm{OP} \perp \mathrm{TP} \) and \( \mathrm{OQ} \perp \mathrm{TQ} \)
And therefore,
\(\angle \mathrm{OPT}=90^{\circ}\)
\(\angle \mathrm{OQT}=90^{\circ}\)
In quadrilateral \(\mathrm{POQT}\) ,
Sum of all interior angles \( =360^{\circ} \)
\(\angle \mathrm{OPT}+\angle \mathrm{POQ}+\angle \mathrm{OQT}+\angle \mathrm{PTQ}=360^{\circ}\)
\(90^{\circ}+110^{\circ}+90^{\circ}+\angle \mathrm{PTQ}=360^{\circ}\)
\(\angle \mathrm{PTQ}=\mathbf{7 0}^{\circ}\)
Given: \(\mathrm{PA}\) and \(\mathrm{PB}\) are tangents.
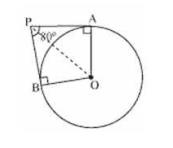
Therefore, the radius drawn to these tangents will be perpendicular to the tangents.
Thus, \( \mathrm{OA} \perp \mathrm{PA} \) and \( \mathrm{OB} \perp \mathrm{PB} \)
\(\angle \mathrm{OBP}=90^{\circ}\)
\(\angle \mathrm{OAP}=90^{\circ}\)
In quadrilateral \(\mathrm{AOBP}\),
Sum of all interior angles \( =360^{\circ} \)
\(\angle \mathrm{OAP}+\angle \mathrm{APB}+\angle \mathrm{PBO}+\angle \mathrm{BOA}=360^{\circ} 90^{\circ}+80^{\circ}+90^{\circ}+\angle \mathrm{BOA}=\)
\(360^{\circ}\)
\(\angle \mathrm{BOA}=100^{\circ}\)
In \( \triangle \mathrm{OPB} \) and \( \triangle \mathrm{OPA} \),
\( \mathrm{AP}=\mathrm{BP} \) (Tangents from a point)
\( \mathrm{OA}=\mathrm{OB} \) (Radii of the circle)
\( \mathrm{OP}=\mathrm{OP}( \) Common side \( ) \)
Therefore, \( \triangle \mathrm{OPB} \cong \triangle \mathrm{OPA} \) (SSS congruence criterion)
And thus, \( \angle \mathrm{POB}=\angle \mathrm{POA} \)
\(\angle P O A=\frac{1}{2} \angle A O B=\frac{100}{2}=50^{\circ}\)

Therefore, the radius drawn to these tangents will be perpendicular to the tangents.
Thus, \( \mathrm{OA} \perp \mathrm{PA} \) and \( \mathrm{OB} \perp \mathrm{PB} \)
\(\angle \mathrm{OBP}=90^{\circ}\)
\(\angle \mathrm{OAP}=90^{\circ}\)
In quadrilateral \(\mathrm{AOBP}\),
Sum of all interior angles \( =360^{\circ} \)
\(\angle \mathrm{OAP}+\angle \mathrm{APB}+\angle \mathrm{PBO}+\angle \mathrm{BOA}=360^{\circ} 90^{\circ}+80^{\circ}+90^{\circ}+\angle \mathrm{BOA}=\)
\(360^{\circ}\)
\(\angle \mathrm{BOA}=100^{\circ}\)
In \( \triangle \mathrm{OPB} \) and \( \triangle \mathrm{OPA} \),
\( \mathrm{AP}=\mathrm{BP} \) (Tangents from a point)
\( \mathrm{OA}=\mathrm{OB} \) (Radii of the circle)
\( \mathrm{OP}=\mathrm{OP}( \) Common side \( ) \)
Therefore, \( \triangle \mathrm{OPB} \cong \triangle \mathrm{OPA} \) (SSS congruence criterion)
And thus, \( \angle \mathrm{POB}=\angle \mathrm{POA} \)
\(\angle P O A=\frac{1}{2} \angle A O B=\frac{100}{2}=50^{\circ}\)
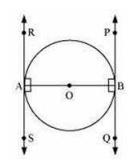
Let \(\mathrm{AB}\) is diameter of the circle. Two tangents \(\mathrm{PQ}\) and \(\mathrm{RS}\) are drawn at points \(\mathrm{A}\) and \(\mathrm{B}\) respectively. Radius drawn to these tangents will be perpendicular to the tangents.
Thus, \( \mathrm{OA} \perp \mathrm{RS} \) and \( \mathrm{OB} \perp \mathrm{PQ} \)
\(\angle \mathrm{OAR}=90^{\circ}\)
\(\angle \mathrm{OAS}=90^{\circ}\)
\(\angle \mathrm{OBP}=90^{\circ}\)
\(\angle \mathrm{OBQ}=90^{\circ}\)
It can be observed that
\( \angle \mathrm{OAR}=\angle \mathrm{OBQ} \) (Alternate interior angles)
\( \angle \mathrm{OAS}=\angle \mathrm{OBP} \) (Alternate interior angles)
Since alternate interior angles are equal, lines \(\mathrm{PQ}\) and \(\mathrm{RS}\) will be parallel.
CBSE Class 10 maths chapter 10 Ex 10.2 || NCERT Solutions for Class 10 Maths Chapter 10 Exercise 10.2
To Prove: A line drawn perpendicular from \(\mathrm{P}\) will pass from
\(\mathrm{O}\).
Given: \(\mathrm{APB}\) is tangent to circle with centre \(\mathrm{O}\).
Let us consider a circle with centre \(\mathrm{O}\). Let \(\mathrm{AB}\) be a tangent which touches the circle at \(\mathrm{P}\).
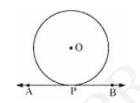
Proof:
Assume that the perpendicular to \(\mathrm{AB}\) at \(\mathrm{P}\) does not pass through centre \(\mathrm{O}\). Let it pass through another point \(\mathrm{O}^\prime\). Join \(\mathrm{OP}\) and \(\mathrm{O}^\prime\mathrm{P}\).
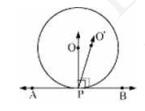
As perpendicular to \(\mathrm{AB}\) at \(\mathrm{P}\) passes through \( \mathrm{O}^{\prime} \), therefore, \( \angle \mathrm{O}^{\prime} \mathrm{PB}=90^{\circ} \ldots(1)\)
\(\mathrm{O}\) is the centre of the circle and \(\mathrm{P}\) is the point of contact. We know the line joining the centre and the point of contact to the tangent of the circle are perpendicular to each other.
\( \therefore \angle \mathrm{OPB}=90^{\circ} \dots(2)\)
Comparing equations \((1)\) and \((2)\), we obtain
\( \angle \mathrm{O}^{\prime} \mathrm{PB}=\angle \mathrm{OPB} \dots(3)\)
From the figure, it can be observed that,
\( \angle \mathrm{O}^{\prime} \mathrm{PB} < \angle \mathrm{OPB} \dots(4)\)
Therefore, \( \angle \mathrm{O}^{\prime} \mathrm{PB}=\angle \mathrm{OPB} \) is not possible. It is only possible, when the line \( \mathrm{O}^{\prime} \mathrm{P} \) coincides with \(\mathrm{OP}\).
Therefore, the perpendicular to \(\mathrm{AB}\) through \(\mathrm{P}\) passes through centre \(\mathrm{O}\).
Hence, Proved.
Given: \(\mathrm{APB}\) is tangent to circle with centre \(\mathrm{O}\).
Let us consider a circle with centre \(\mathrm{O}\). Let \(\mathrm{AB}\) be a tangent which touches the circle at \(\mathrm{P}\).

Proof:
Assume that the perpendicular to \(\mathrm{AB}\) at \(\mathrm{P}\) does not pass through centre \(\mathrm{O}\). Let it pass through another point \(\mathrm{O}^\prime\). Join \(\mathrm{OP}\) and \(\mathrm{O}^\prime\mathrm{P}\).

As perpendicular to \(\mathrm{AB}\) at \(\mathrm{P}\) passes through \( \mathrm{O}^{\prime} \), therefore, \( \angle \mathrm{O}^{\prime} \mathrm{PB}=90^{\circ} \ldots(1)\)
\(\mathrm{O}\) is the centre of the circle and \(\mathrm{P}\) is the point of contact. We know the line joining the centre and the point of contact to the tangent of the circle are perpendicular to each other.
\( \therefore \angle \mathrm{OPB}=90^{\circ} \dots(2)\)
Comparing equations \((1)\) and \((2)\), we obtain
\( \angle \mathrm{O}^{\prime} \mathrm{PB}=\angle \mathrm{OPB} \dots(3)\)
From the figure, it can be observed that,
\( \angle \mathrm{O}^{\prime} \mathrm{PB} < \angle \mathrm{OPB} \dots(4)\)
Therefore, \( \angle \mathrm{O}^{\prime} \mathrm{PB}=\angle \mathrm{OPB} \) is not possible. It is only possible, when the line \( \mathrm{O}^{\prime} \mathrm{P} \) coincides with \(\mathrm{OP}\).
Therefore, the perpendicular to \(\mathrm{AB}\) through \(\mathrm{P}\) passes through centre \(\mathrm{O}\).
Hence, Proved.
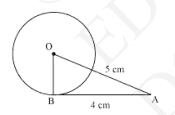
Let us consider a circle centred at point \(\mathrm{O}\).
\(\mathrm{AB}\) is a tangent drawn on this circle from point \(\mathrm{A}\).
Given that,
\( \mathrm{OA}=5 \mathrm{~cm} \) and \( \mathrm{AB}=4 \mathrm{~cm} \)
In \( \triangle \mathrm{ABO} \),
\( \mathrm{OB} \perp \mathrm{AB} \) (Radius \( \perp \) tangent at the point of contact)
Applying Pythagoras theorem in \( \triangle \mathrm{ABO} \), we obtain
\(\mathrm{AB}^{2}+\mathrm{BO}^{2}=\mathrm{OA}^{2}\)
\(4^{2}+\mathrm{BO}^{2}=5^{2}\)
\(16+\mathrm{BO}^{2}=25\ \mathrm{BO}^{2}=9\)
\(\mathrm{BO}=3\)
Hence, the radius of the circle is \(3\) cm .
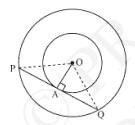
Let the two concentric circles be centred at point \(\mathrm{O}\). And let \(\mathrm{PQ}\) be the chord of the larger circle which touches the smaller circle at point A. Therefore, \(\mathrm{PQ}\) is tangent to the smaller circle.
\( \mathrm{OA} \perp \mathrm{PQ}\) (As \( \mathrm{OA} \) is the radius of the circle)
Applying Pythagoras theorem in \( \triangle \mathrm{OAP} \), we obtain
\(\mathrm{OA}^{2}+\mathrm{AP}^{2}=\mathrm{OP}^{2}\)
\(3^{2}+\mathrm{AP}^{2}=5^{2}\)
\(9+\mathrm{AP}^{2}=25\)
\(\mathrm{AP}^{2}=16\)
\(\mathrm{AP}=4\)
In \( \triangle \mathrm{OPQ} \),
Since \( \mathrm{OA} \perp \mathrm{PQ} \),
\( \mathrm{AP}=\mathrm{AQ} \) (Perpendicular from the centre of the circle bisects the chord)
\(\mathrm{PQ}=2 \mathrm{AP}=2 \times 4=8\)
Therefore, the length of the chord of the larger circle is \(8\) cm.
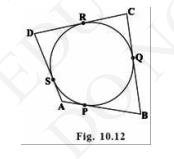
To Prove: \( \mathrm{AB}+\mathrm{CD}=\mathrm{AD}+\mathrm{BC} \)
Proof:
In the given figure, it can be observed that \(\mathrm{AB}\) touches the circle at point \( \mathrm{P} ; \mathrm{BC} \) touches the circle at point \( \mathrm{Q} ; \mathrm{CD} \) touches the circle at point \(\mathrm{R}\); \(\mathrm{DA}\) touches the circle at point \(\mathrm{S}\).
Then, we can say from a theorem that "Length of tangents drawn from an external point to the circle are same", Therefore,
\( \mathrm{DR}=\mathrm{DS} \) (Tangents on the circle from point D ) \(\dots(1)\)
\( \mathrm{CR}=\mathrm{CQ} \) (Tangents on the circle from point C ) \(\dots(2)\)
\( \mathrm{BP}=\mathrm{BQ}( \) Tangents on the circle from point B\( ) \) \(\dots(3)\)
\( \mathrm{AP}=\mathrm{AS} \) (Tangents on the circle from point A )\(\dots(4)\)
Adding all these equations, we obtain
\(\mathrm{DR}+\mathrm{CR}+\mathrm{BP}+\mathrm{AP}=\mathrm{DS}+\mathrm{CQ}+\mathrm{BQ}+\mathrm{AS}\)
\((\mathrm{DR}+\mathrm{CR})+(\mathrm{BP}+\mathrm{AP})=(\mathrm{DS}+\mathrm{AS})+(\mathrm{CQ}+\mathrm{BQ})\)
\(\mathrm{CD}+\mathrm{AB}=\mathrm{AD}+\mathrm{BC}\)
Hence, Proved.
CBSE Class 10 maths chapter 10 Ex 10.2 || NCERT Solutions for Class 10 Maths Chapter 10 Exercise 10.2
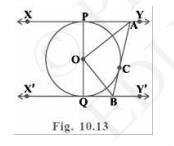
Let us join point \(\mathrm{O}\) to \(\mathrm{C}\) .
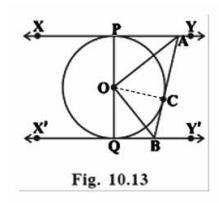
In \( \triangle \mathrm{OPA} \) and \( \triangle \mathrm{OCA} \)
\( \mathrm{OP}=\mathrm{OC}( \) Radius of the same circle \( ) \)
\( \mathrm{AP}=\mathrm{AC}( \) Tangents from point A\( ) \)
\( \mathrm{AO}=\mathrm{AO} \) (Common side)
\( \triangle \mathrm{OPA} \cong \Delta \mathrm{OCA}\) (SSS congruence criterion)
\( \angle \mathrm{POA}=\angle \mathrm{COA} \ldots(i) \)
Similarly, \( \triangle \mathrm{OQB} \cong \Delta \mathrm{OCB} \)
\( \angle \mathrm{QOB}=\angle \mathrm{COB} \ldots( ii)\)
Since \(\mathrm{POQ}\) is a diameter of the circle, it is a straight line.
Therefore, \( \angle \mathrm{POA}+\angle \mathrm{COA}+\angle \mathrm{COB}+\angle \mathrm{QOB}=180^{\circ} \)
From equations \((i)\) and \((ii)\), it can be observed that \( 2 \angle \mathrm{COA}+2 \angle \mathrm{COB}=180^{\circ}\)
\(\angle \mathrm{COA}+\angle \mathrm{COB}=\frac{ 180^{\circ} }{ 2 }\)
\(\angle \mathrm{COA}+\angle \mathrm{COB}=90^{\circ}\)
\(\angle \mathrm{AOB}=90^{\circ}\)
Hence Proved.

In \( \triangle \mathrm{OPA} \) and \( \triangle \mathrm{OCA} \)
\( \mathrm{OP}=\mathrm{OC}( \) Radius of the same circle \( ) \)
\( \mathrm{AP}=\mathrm{AC}( \) Tangents from point A\( ) \)
\( \mathrm{AO}=\mathrm{AO} \) (Common side)
\( \triangle \mathrm{OPA} \cong \Delta \mathrm{OCA}\) (SSS congruence criterion)
\( \angle \mathrm{POA}=\angle \mathrm{COA} \ldots(i) \)
Similarly, \( \triangle \mathrm{OQB} \cong \Delta \mathrm{OCB} \)
\( \angle \mathrm{QOB}=\angle \mathrm{COB} \ldots( ii)\)
Since \(\mathrm{POQ}\) is a diameter of the circle, it is a straight line.
Therefore, \( \angle \mathrm{POA}+\angle \mathrm{COA}+\angle \mathrm{COB}+\angle \mathrm{QOB}=180^{\circ} \)
From equations \((i)\) and \((ii)\), it can be observed that \( 2 \angle \mathrm{COA}+2 \angle \mathrm{COB}=180^{\circ}\)
\(\angle \mathrm{COA}+\angle \mathrm{COB}=\frac{ 180^{\circ} }{ 2 }\)
\(\angle \mathrm{COA}+\angle \mathrm{COB}=90^{\circ}\)
\(\angle \mathrm{AOB}=90^{\circ}\)
Hence Proved.
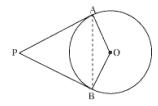
To Prove: \( \angle \mathrm{APB}+\angle \mathrm{BOA}=180^{\circ} \)
Proof: Let us consider a circle centred at point \(\mathrm{O}\).
Let \(\mathrm{P}\) be an external point from which two tangents \(\mathrm{PA}\) and \(\mathrm{PB}\) are drawn to the circle which touches the circle at point \(\mathrm{A}\) and \(\mathrm{B}\) respectively and \(\mathrm{AB}\) is the line segment, joining point of contacts \(\mathrm{A}\) and \(\mathrm{B}\) together such that it subtends
\( \angle \mathrm{AOB} \) at centre \(\mathrm{O}\) of the circle.
It can be observed that
\( \mathrm{OA} \perp \mathrm{PA} \) (radius of circle is always perpendicular to tangent)
Therefore, \( \angle \mathrm{OAP}=90^{\circ} \)
Similarly, \( \mathrm{OB} \perp \mathrm{PB} \)
\( \angle \mathrm{OBP}=90^{\circ} \)
In quadrilateral \(\mathrm{OAPB}\)
Sum of all interior angles \( =360^{\circ} \)
\(\angle \mathrm{OAP}+\angle \mathrm{APB}+\angle \mathrm{PBO}+\angle \mathrm{BOA}=360^{\circ}\)
\(90^{\circ}+\angle \mathrm{APB}+90^{\circ}+\angle \mathrm{BOA}=360^{\circ}\)
\(\angle \mathrm{APB}+\angle \mathrm{BOA}=180^{\circ}\)
Hence, it can be observed that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line-segment joining the points of contact at the centre.
Since \(\mathrm{ABCD}\) is a parallelogram,
\(\mathrm{AB}=\mathrm{CD}\ldots(1)\)
\(\mathrm{BC}=\mathrm{AD}\ldots(2)\)
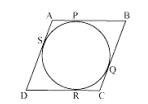
It can be observed that
\( \mathrm{DR}=\mathrm{DS} \) (Tangents on the circle from point D )
\( \mathrm{CR}=\mathrm{CQ} \) (Tangents on the circle from point C )
\( \mathrm{BP}=\mathrm{BQ}( \) Tangents on the circle from point B\( ) \)
\( \mathrm{AP}=\mathrm{AS} \) (Tangents on the circle from point A )
Adding all these equations, we obtain
\(\mathrm{DR}+\mathrm{CR}+\mathrm{BP}+\mathrm{AP}=\mathrm{DS}+\mathrm{CQ}+\mathrm{BQ}+\mathrm{AS}\)
\((\mathrm{DR}+\mathrm{CR})+(\mathrm{BP}+\mathrm{AP})=(\mathrm{DS}+\mathrm{AS})+(\mathrm{CQ}+\mathrm{BQ})\)
\(\mathrm{CD}+\mathrm{AB}=\mathrm{AD}+\mathrm{BC}\)
On putting the values of equations \((1)\) and \((2)\) in this equation, we obtain \( 2 \mathrm{AB}=2 \mathrm{BC} \)
\(\mathrm{AB}=\mathrm{BC} \ldots(3)\)
Comparing equations \((1)\), \((2)\), and \((3)\), we obtain
\(\mathrm{AB}=\mathrm{BC}=\mathrm{CD}=\mathrm{DA}\)
Hence, \(\mathrm{ABCD}\) is a rhombus.
\(\mathrm{AB}=\mathrm{CD}\ldots(1)\)
\(\mathrm{BC}=\mathrm{AD}\ldots(2)\)

It can be observed that
\( \mathrm{DR}=\mathrm{DS} \) (Tangents on the circle from point D )
\( \mathrm{CR}=\mathrm{CQ} \) (Tangents on the circle from point C )
\( \mathrm{BP}=\mathrm{BQ}( \) Tangents on the circle from point B\( ) \)
\( \mathrm{AP}=\mathrm{AS} \) (Tangents on the circle from point A )
Adding all these equations, we obtain
\(\mathrm{DR}+\mathrm{CR}+\mathrm{BP}+\mathrm{AP}=\mathrm{DS}+\mathrm{CQ}+\mathrm{BQ}+\mathrm{AS}\)
\((\mathrm{DR}+\mathrm{CR})+(\mathrm{BP}+\mathrm{AP})=(\mathrm{DS}+\mathrm{AS})+(\mathrm{CQ}+\mathrm{BQ})\)
\(\mathrm{CD}+\mathrm{AB}=\mathrm{AD}+\mathrm{BC}\)
On putting the values of equations \((1)\) and \((2)\) in this equation, we obtain \( 2 \mathrm{AB}=2 \mathrm{BC} \)
\(\mathrm{AB}=\mathrm{BC} \ldots(3)\)
Comparing equations \((1)\), \((2)\), and \((3)\), we obtain
\(\mathrm{AB}=\mathrm{BC}=\mathrm{CD}=\mathrm{DA}\)
Hence, \(\mathrm{ABCD}\) is a rhombus.
CBSE Class 10 maths chapter 10 Ex 10.2 || NCERT Solutions for Class 10 Maths Chapter 10 Exercise 10.2
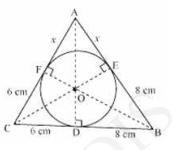
To Find: \(\mathrm{AB}\) and \(\mathrm{AC}\)
Let the given circle touch the sides \(\mathrm{AB}\) and \(\mathrm{AC}\) of the triangle at point \(\mathrm{E}\) and \(\mathrm{F}\) respectively and the length of the line segment \(\mathrm{AF}\) be \(x\).
In \( \triangle \mathrm{ABC} \),
From the theorem which states that the lengths of two tangents drawn from an external point to a circle are equal.
So,
\( \mathrm{CF}=\mathrm{CD}=6 \mathrm{~cm}( \) Tangents on the circle from point C )
\( \mathrm{BE}=\mathrm{BD}=8 \mathrm{~cm}( \) Tangents on the circle from point B\( ) \)
\( \mathrm{AE}=\mathrm{AF}=x( \) Tangents on the circle from point A\( ) \)
\( \mathrm{AB}=\mathrm{AE}+\mathrm{EB}=x+8 \)
\( \mathrm{BC}=\mathrm{BD}+\mathrm{DC}=8+6=14 \)
\( \mathrm{CA}=\mathrm{CF}+\mathrm{FA}=6+x \)
By heron's formula
\(\text { area of } \triangle A B C=\sqrt{s(s-a)(s-b)(s-c)}\)
where, \( \mathrm{a}, \mathrm{b} \) and \(\mathrm{c}\) are sides of triangle and \(\mathrm{s}\) is semi perimeter.
\(2 S=\mathrm{AB}+\mathrm{BC}+\mathrm{CA}\)
\(=x+8+14+6+x\)
\(=28+2 x\)
\(S=\frac{28+2 x}{2}=14+x\)
\(\text { area of } \triangle A B C=\sqrt{s(s-a)(s-b)(s-c)}\)
\(=\sqrt{\{14+x\}\{x\}(8)(6)}\)
\(=4 \sqrt{3\left(14 x+x^{2}\right)}\)
Also, area of triangle \( =\frac{1}{2} \times \) base \( \times \) height
And from the given figure it is clear that Area of \( \triangle \mathrm{ABC}= \) Area of \( \Delta \mathrm{OBC}+ \) Area of \( \Delta \mathrm{OCA}+ \) Area of \( \Delta \mathrm{OAB} \)
Area of \( \triangle O B C=\frac{1}{2} \times O D \times B C=\frac{1}{2} \times 4 \times 14=28 \)
Area of \( \triangle O C A=\frac{1}{2} \times O F \times A C=\frac{1}{2} \times 4 \times(6+x)=12+2 x \)
Area of \( \triangle O C A=\frac{1}{2} \times O E \times A B=\frac{1}{2} \times 4 \times(8+x)=16+2 x \)
Area of \( \triangle \mathrm{ABC}= \) Area of \( \triangle \mathrm{OBC}+ \) Area of \( \triangle \mathrm{OCA}+ \) Area of \( \triangle \mathrm{OAB} \)
\(\Rightarrow 4 \sqrt{3\left(14 x+x^{2}\right)}=28+12+2 x+16+2 x\)
\(\Rightarrow 4 \sqrt{3\left(14 x+x^{2}\right)}=56+4 x\)
\(=\sqrt{3\left(14 x+x^{2}\right)}=14+x\)
\(\Rightarrow 3 x(14+x)=(14+x)^{2}\)
\(\Rightarrow 3 x=14+x\)
\(\Rightarrow 2 x=14\)
\(\Rightarrow x=7\)
Therefore, \( x=7 \)
Hence,
\(\mathrm{AB}=x+8=7+8=15 \mathrm{~cm}\)
\(\mathrm{CA}=6+x=6+7=13 \mathrm{~cm}\)
Hence, \( \mathrm{AB}=15 \mathrm{~cm} \) and \( \mathrm{AC}=13 \mathrm{~cm} \)
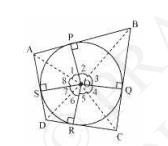
To Prove: \( \angle \mathrm{AOB}+\angle \mathrm{COD}=180^{\circ}, \angle \mathrm{BOC}+\angle \mathrm{DOA}=180^{\circ} \)
Given: \(\mathrm{ABCD}\) is circumscribing the circle.
Proof: Let \(\mathrm{ABCD}\) be a quadrilateral circumscribing a circle centred at \(\mathrm{O}\) such that it touches the circle at point \(\mathrm{P,Q,R,S}\).
Join the vertices of the quadrilateral \(\mathrm{ABCD}\) to the centre of the circle.
Consider \( \triangle \mathrm{OAP} \) and \( \triangle \mathrm{OAS} \),
\( \mathrm{AP}=\mathrm{AS} \) (Tangents from the same point)
\(\mathrm{OP} =\mathrm{OS}\) (Radii of the same circle)
\( \mathrm{OA}=\mathrm{OA}( \) Common side)
\( \Delta \mathrm{OAP} \cong \Delta \mathrm{OAS} \) (SSS congruence criterion)
And thus, \( \angle \mathrm{POA}=\angle \mathrm{AOS} \)
\(\angle 1=\angle 8 \text { Similarly, }\)
\(\angle 2=\angle 3\)
\(\angle 4=\angle 5\)
\(\angle 6=\angle 7\)
\(\angle 1+\angle 2+\angle 3+\angle 4+\angle 5+\angle 6+\angle 7+\angle 8=360^{\circ}\)
\((\angle 1+\angle 8)+(\angle 2+\angle 3)+(\angle 4+\angle 5)+(\angle 6+\angle 7)=360^{\circ}\)
\(2 \angle 1+2 \angle 2+2 \angle 5+2 \angle 6=360^{\circ}\)
\(2(\angle 1+\angle 2)+2(\angle 5+\angle 6)=360^{\circ}\)
\((\angle 1+\angle 2)+(\angle 5+\angle 6)=180^{\circ}\)
\(\angle \mathrm{AOB}+\angle \mathrm{COD}=180^{\circ}\)
Similarly, we can prove that \( \angle \mathrm{BOC}+\angle \mathrm{DOA}=180^{\circ} \)
Hence, opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.