Ncert solutions for class 9 maths chapter 6 exercise 6.3 || rd sharma class 9 Lines and Angles || ex 6.3 class 9 maths ncert solutions || exercise 6.3 class 9 maths ncert solutions
Explore detailed, step-by-step solutions for Class 9 Maths Chapter 6, Exercise 6.3, which focuses on further applications of Lines and Angles. This exercise builds upon students’ understanding of angle relationships when a transversal intersects two lines, especially in the context of identifying whether lines are parallel. It emphasizes the use of properties such as alternate interior angles, corresponding angles, and vertically opposite angles to prove geometrical statements. By engaging with Exercise 6.3, learners refine their logical reasoning, improve their proof-writing skills, and gain confidence in handling problems involving angle relationships — forming a strong foundation for advanced geometry in higher classes.

ncert solutions for class 9 maths chapter 6 exercise 6.3 || rd sharma class 9 Lines and Angles || ex 6.3 class 9 maths ncert solutions || exercise 6.3 class 9 maths ncert solutions
Exercise 6.3
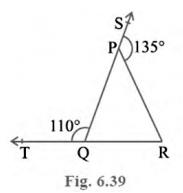
1. In Fig. 6.39, sides \(QP\) and \(RQ\) of \( \triangle {PQR} \)
are produced to points \( S \) and \(T\) respectively. If \(
\angle {SPR}=135^{\circ} \) and \( \angle {PQT}=110^{\circ} \),
find \( \angle PRQ\).

Answer
Method 1:It is given in the question that:
\(\angle {SPR}=135^{\circ}\)
And,
\(\angle {PQT}=110^{\circ}\)
Now, according to the question,
\(\angle {SPR}+\angle {QPR}=180^{\circ}({SQ} \text { is a straight line})\)
\(135^{\circ}+\angle {QPR}=180^{\circ}\)
\(\angle {QPR}=45^{\circ}\)
And,
\( \angle {PQT}+\angle {PQR}=180^{\circ} \) (TR is a straight line)
\(110^{\circ}+\angle {PQR}=180^{\circ}\)
\(\angle {PQR}=70^{\circ}\)
Now,
\( \angle {PQR}+\angle {QPR}+\angle {PRQ}=180^{\circ} \) (Sum of the interior angles of the triangle)
\(70^{\circ}+45^{\circ}+\angle {PRQ}=180^{\circ}\)
\(115^{\circ}+\angle {PRQ}=180^{\circ}\)
\(\angle {PRQ}=65^{\circ}\)
Method 2:
It is given in the question that:
\(\angle {SPR}=135^{\circ}\)
And,
\(\angle {PQT}=110^{\circ}\)
\(\angle {PQT}+\angle {PQR}=180^{\circ}({TR} \text { is a straight line})\)
\(110^{\circ}+\angle {PQR}=180^{\circ}\)
\(\angle {PQR}=70^{\circ}\)
Now, we know that the exterior angle of the triangle equals the sum of interior opposite angles.
Therefore, \( \angle {SPR}=\angle {PQR}+\angle {PRQ} \)
\(135^{\circ}=70^{\circ}+\angle {PRQ}\)
\(\angle {PRQ}=65^{\circ}\)
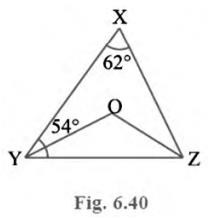
2. In Fig. 6.40, \( \angle X=62^{\circ}, \angle X Y Z=54^{\circ}
\). If \(YO\) and \(ZO\) are the bisectors of \( \angle {XYZ} \)
and \( \angle {XZY} \) respectively of \( \triangle {XYZ} \), find
\( \angle {OZY} \) and \( \angle {YOZ} \).

Answer
Given: \( \angle X=62^{\circ}, \angle X Y Z=54^{\circ} \)\(YO\) and \(ZO\) are the bisectors of \( \angle {XYZ} \) and \( \angle {XZY} \) respectively.
To Find: \( \angle {OZY} \) and \( \angle {YOZ} \).
Now, according to the question,
\(\angle X+\angle X Y Z+\angle X Z Y=180^{\circ}\) \( \ (\text {Sum of the interior angles of a triangle} =180^{\circ})\)
\(62^{\circ}+54^{\circ}+\angle X Z Y=180^{\circ}\)
\(116^{\circ}+\angle X Z Y=180^{\circ}\)
\(\angle X Z Y=64^{\circ}\)
Now,
As \(ZO\) is the bisector of \( \angle {XZY} \)
\(\angle {OZY}=\frac{1}{2} \angle {XZY}\)
\(\angle {OZY}=32^{\circ}\)
And,
As \(YO\) is bisector of \( \angle {XYZ} \)
\(\angle {OYZ}=\frac{1}{2} \angle {XYZ}\)
\(\angle {OYZ}=27^{\circ}\)
Now,
\(\angle {OZY}+\angle {OYZ}+\angle {O}=180^{\circ}\) \( \left(\right. \)Sum of the interior angles of the triangle \( \left.=180^{\circ}\right) \)
\(=32^{\circ}+27^{\circ}+\angle {O}=180^{\circ}\)
\(=59^{\circ}+\angle {O}=180^{\circ}\)
\(=\angle {O}=121^{\circ}\)
ncert solutions for class 9 maths chapter 6 exercise 6.3 || rd sharma class 9 Lines and Angles || ex 6.3 class 9 maths ncert solutions || exercise 6.3 class 9 maths ncert solutions
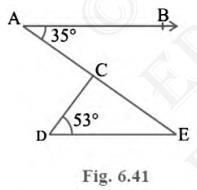
3. In Fig. 6.41, if \( {AB} \| {DE}, \angle {BAC}=35^{\circ} \)
and \( \angle {CDE}=53^{\circ} \), find \( \angle DCE\).

Answer
Given: \(AB\) parallel \( {DE}, \angle {BAC}=35^{\circ}, \angle
{CDE}=53^{\circ} \)To Find: \( \angle D C E \)
According to question,
\( \angle {BAC}=\angle {CED} \) (Alternate interior angles)
Therefore,
\(\angle C E D=35^{\circ}\)
Now, In \( \triangle {DEC} \),
\(\angle {DCE}+\angle {CED}+\angle {CDE}=180^{\circ}\) (Sum of the interior angles of the triangle)
\(\angle {DCE}+35^{\circ}+53^{\circ}=180^{\circ}\)
\(\angle {DCE}+88^{\circ}=180^{\circ}\)
\(\angle {DCE}=92^{\circ}\)
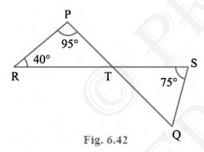
4. In Fig. 6.42, if lines \(PQ\) and \(RS\) intersect at point
\(T\), such that \( \angle {PRT}=40^{\circ}, \angle
{RPT}=95^{\circ} \) and \( \angle {TSQ}=75^{\circ} \), find \(
\angle {SQT} \).

Answer
Given:\(\angle {PRT}=40^{\circ}\)
\(\angle {RPT}=95^{\circ} \text { and, }\)
\(\angle {TSQ}=75^{\circ}\)
Now according to the question,
\( \angle {PRT}+\angle {RPT}+\angle {PTR}=180^{\circ} \) (Sum of interior angles of the triangle)
\(40^{\circ}+95^{\circ}+\angle {PTR}=180^{\circ}\)
\(40^{\circ}+95^{\circ}+\angle {PTR}=180^{\circ}\)
\(135^{\circ}+\angle {PTR}=180^{\circ}\)
\(\angle {PTR}=45^{\circ}\)
\(\angle {PTR}=\angle {STQ}=45^{\circ} \text { (Vertically opposite angles) }\)
Now,
\( \angle {TSQ}+\angle {PTR}+\angle {SQT}=180^{\circ} \) (Sum of the interior angles of the triangle)
\(75^{\circ}+45^{\circ}+\angle {SQT}=180^{\circ}\)
\(120^{\circ}+\angle {SQT}=180^{\circ}\)
\(\angle {SQT}=60^{\circ}\)
5. In Fig. 6.43, if \( {PQ} \perp {PS}, {PQ} \| {SR}, \angle
{SQR}=28^{\circ} \) and \( \angle {QRT} \) \( =65^{\circ} \), then
find the values of \( x \) and \( y \).
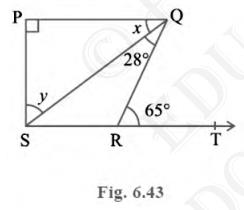

Answer
To Find: Values of \( x \) and \( y \)Given: \(PQ\) is perpendicular to \(PS , PQ\) parallel \(SR\)
\(\angle {SQR}=28^{\circ}\)
And, \( \angle {QRT}=65^{\circ} \)
Now according to the question,
\( {x}+\angle {SQR}=\angle {QRT} \) (Alternate angles are equal as \(QR\) is transversal)
\(x+28^{\circ}=65^{\circ}\)
\(x=37^{\circ}\)
Now, in \( \triangle {PQS} \), Sum of interior angles of a triangle \( =180^{\circ} \)
\(\angle {PQS}+\angle {PSQ}+\angle {QPS}=180^{\circ} \text { Therefore, }\)
\({y}+37^{\circ}+90^{\circ}=180^{\circ}\)
\({y}=53^{\circ} \text { So } {x}=37^{\circ} \text { and } {y}=53^{\circ}\)
6. In Fig. 6.44, the side \( Q R \) of \( \triangle P Q R \) is
produced to a point \( S \). If the bisectors of \( \angle {PQR}
\) and \( \angle {PRS} \) meet at point \(T \), then prove that \(
\angle {QTR} \) \( =\frac{ 1 }{ 2 } \angle {QPR} \).
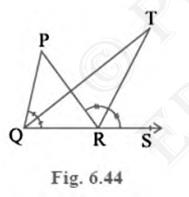

Answer
To Prove: \( \angle {QTR}=\frac{1}{2} \angle {QPR} \)Given: Bisectors of \( \angle {PQR} \) and \( \angle {PRS} \) meet at point \(T\)
Proof:
In \( \triangle {QTR} \),
\( \angle {TRS}=\angle {TQR}+\angle {QTR} \) (Exterior angle of a triangle equals to the sum of the two opposite interior angles)
\( \angle {QTR}=\angle {TRS}-\angle {TQR}\quad \ldots\ldots\text{(i)} \)
Similarly, in \( \triangle {QPR} \),
\( \angle {SRP}=\angle {QPR}+\angle {PQR} \)
\( 2 \angle {TRS}=\angle {QPR}+2 \angle {TQR} \) (\( \because \angle {TRS} \) and \( \angle {TQR} \) are the bisectors of \( \angle {SRP} \) and \( \angle {PQR} \) respectively.)
\( \angle {QPR}=2 \angle {TRS}-2 \angle {TQR} \)
\( \angle {TRS}-\angle {TQR}=\frac{1}{2} \angle {QPR} \quad \ldots\ldots\text{(ii)}\)
From (i) and (ii), we get
\(\angle {QTR}=\frac{1}{2} \angle {QPR}\)
Hence, proved.

