Exercise 7.1 maths class 9 || maths chapter 7 class 9 exercise 7.1 || exercise 7.1 class 9 maths || rd sharma class 9 triangle || chapter 7 maths class 9 exercise 7.1 || class 9 ncert exercise 7.1 || chapter 7 exercise 7.1 class 9 || class 9 maths chapter 7 exercise 7.1 solutions || ncert class 9 exercise 7.1
Explore detailed, step-by-step solutions for Class 9 Maths Chapter 7, Exercise 7.1, centered on the topic of Triangles. This exercise introduces students to the fundamental properties and classification of triangles based on sides and angles. It lays the groundwork for understanding congruence in triangles by guiding learners through problems involving angle sum property, exterior angle theorem, and basic triangle properties. By working through Exercise 7.1, students strengthen their logical thinking, apply geometric rules systematically, and build a solid conceptual base for more advanced topics such as congruence and inequalities in triangles in later chapters and higher classes.

exercise 7.1 maths class 9 || maths chapter 7 class 9 exercise 7.1 || exercise 7.1 class 9 maths || rd sharma class 9 triangle || chapter 7 maths class 9 exercise 7.1 || class 9 ncert exercise 7.1 || chapter 7 exercise 7.1 class 9 || class 9 maths chapter 7 exercise 7.1 solutions || ncert class 9 exercise 7.1
Exercise 7.1
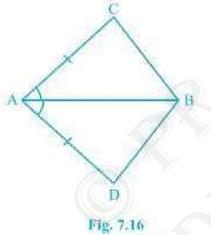
1. In quadrilateral \( \mathrm{ACBD}, \mathrm{AC}=\mathrm{AD} \)
and \( \mathrm{AB}\) bisect \(A\) (see Fig. 7.16). Show that \(
\triangle A B C\ \triangle A B D \). What can you say about \( B C
\) and \(BD\)?

Answer
It is given that \( \mathrm{AC}\) and \( \mathrm{AD}\) are equal
i.e. \( \mathrm{AC}=\mathrm{AD} \) and the line segment \(
\mathrm{AB}\) bisects \(A \).We will have to now prove that the two triangles \( A B C \) and \( A B D \) are similar i.e. \( \triangle \mathrm{ABC} \mathrm{\Delta A B D} \)
Proof:
Consider the triangles \( \triangle \mathrm{ABC} \) and \( \triangle \mathrm{ABD} \),
(i) \( \mathrm{AC}=\mathrm{AD} \) (It is given in the question)
(ii) \( \mathrm{AB}=\mathrm{AB}( \) Common)
(iii) \( \mathrm{CAB}=\mathrm{DAB} \) (Since AB is the bisector of angle A )
So, by SAS congruency criterion, \( \triangle \mathrm{ABC} \triangle \mathrm{ABD} \).
For the \( 2^{\text {nd }} \) part of the question, \( \mathrm{BC}\) and \( \mathrm{BD}\) are of equal lengths by the rule of C.P.C.T.
2. \( \mathrm{ABCD}\) is a quadrilateral in which \(
\mathrm{AD}=\mathrm{BC} \) and \( \mathrm{DAB}=\mathrm{CBA} \)
(see Fig. 7.17). Prove that
(i) \( \triangle \mathrm{ABD} \triangle \mathrm{BAC} \) (ii) \( \mathrm{BD}=\mathrm{AC} \) (iii) \( \angle \mathrm{ABD}=\angle \mathrm{BAC} \).
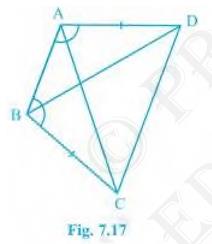
(i) \( \triangle \mathrm{ABD} \triangle \mathrm{BAC} \) (ii) \( \mathrm{BD}=\mathrm{AC} \) (iii) \( \angle \mathrm{ABD}=\angle \mathrm{BAC} \).

Answer
The given parameters from the questions are \(
\mathrm{DAB}=\mathrm{CBA} \) and \( \mathrm{AD}=\mathrm{BC} \).(i) \( \triangle \mathrm{ABD} \) and \( \triangle \mathrm{BAC} \) are similar by SAS congruency as
\( \mathrm{AB}=\mathrm{BA} \) (It is the common arm)
\( \mathrm{DAB}=\mathrm{CBA} \) and \( \mathrm{AD}=\mathrm{BC} \) (These are given in the question)
So, triangles \( \mathrm{ABD}\) and \( \mathrm{BAC}\) are similar i.e. \( \triangle \mathrm{ABD} \triangle \mathrm{BAC} \). (Hence proved).
(ii) It is now known that \( \triangle \mathrm{ABD} \triangle \mathrm{BAC} \) so, \( \mathrm{BD}=\mathrm{AC} \) (by the rule of CPCT).
(iii) Since \( \triangle A B D \triangle B A C \) so,
Angles \( \mathrm{ABD}=\mathrm{BAC} \) (by the rule of CPCT ).
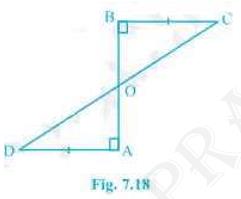
3. \( A D \) and \( B C \) are equal perpendiculars to a line
segment \( A B \) (see Fig. 7.18). Show that \(CD\) bisects
\(AB\).

Answer
It is given that \( A D \) and \( B C \) are two equal
perpendiculars to \( A B \).We will have to prove that \( \mathbf{C D} \) is the bisector of \( \mathbf{A B} \)
Now,
Triangles \( \triangle \mathrm{AOD} \) and \( \triangle \mathrm{BOC} \) are similar by AAS congruency since:
(i) \( \mathrm{A}=\mathrm{B} \quad\) (They are perpendiculars)
(ii) \( \mathrm{AD}=\mathrm{BC} \quad\) (As given in the question)
(iii) \( \mathrm{AOD}=\mathrm{BOC} \quad\) (They are vertically opposite angles)
\( \therefore \triangle \mathrm{AOD} \triangle \mathrm{BOC} \).
So, \( A O=O B \) (by the rule of \( C P C T \) ).
Thus, \(CD\) bisects \(AB\) (Hence proved).
exercise 7.1 maths class 9 || maths chapter 7 class 9 exercise 7.1 || exercise 7.1 class 9 maths || rd sharma class 9 triangle || chapter 7 maths class 9 exercise 7.1 || class 9 ncert exercise 7.1 || chapter 7 exercise 7.1 class 9 || class 9 maths chapter 7 exercise 7.1 solutions || ncert class 9 exercise 7.1
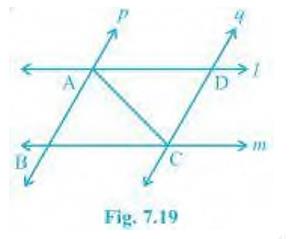
4. \( l \) and \( m \) are two parallel lines intersected by
another pair of parallel lines \( p \) and \( q \) (see Fig.
7.19). Show that \( \triangle A B C \triangle C D A \).

Answer
It is given that p q and 1 mTo prove:
Triangles ABC and CDA are similar i.e. \( \triangle \mathrm{ABC} \triangle \mathrm{CDA} \)
Proof:
Consider the \( \triangle \mathrm{ABC} \) and \( \triangle \mathrm{CDA} \),
(i) \( \mathrm{BCA}=\mathrm{DAC} \) and \( \mathrm{BAC}=\mathrm{DCA} \) Since they are alternate interior angles
(ii) \( \mathrm{AC}=\mathrm{CA} \) as it is the common arm
So, by ASA congruency criterion, \( \triangle \mathrm{ABC} \triangle \mathrm{CDA} \).
5. Line \( l \) is the bisector of an angle \( A \) and \( B \)
is any point on \( l \). \(BP\) and \( B Q \) are perpendiculars
from \( B \) to the arms of \( A \) (see Fig. 7.20). Show that:
(i) \( \triangle \mathrm{APB} \triangle \mathrm{AQB} \)
(ii) \( \mathrm{BP}=\mathrm{BQ} \) or B is equidistant from the arms of A .
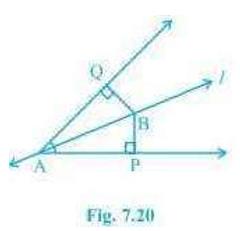
(i) \( \triangle \mathrm{APB} \triangle \mathrm{AQB} \)
(ii) \( \mathrm{BP}=\mathrm{BQ} \) or B is equidistant from the arms of A .

Answer
It is given that the line "\( l \)" is the bisector of angle A and
the line segments BP and BQ are perpendiculars drawn from \( l
\).(i) \( \triangle \mathrm{APB} \) and \( \triangle \mathrm{AQB} \) are similar by AAS congruency because:
\( \mathrm{P}=\mathrm{Q} \) (They are the two right angles)
\( \mathrm{AB}=\mathrm{AB} \) (It is the common arm)
\( \mathrm{BAP}=\mathrm{BAQ}\) (As line \( l \) is the bisector of angle A\( ) \)
So, \( \triangle \mathrm{APB} \triangle \mathrm{AQB} \).
(ii) By the rule of \( \mathrm{CPCT}, \mathrm{BP}=\mathrm{BQ} \). So, it can be said the point B is equidistant from the arms of A .
6. In Fig. 7.21, \( \mathrm{AC}=\mathrm{AE},
\mathrm{AB}=\mathrm{AD} \) and \( \mathrm{BAD}= \mathrm{EAC}\).
Show that \( \mathrm{BC}= \mathrm{DE}\).
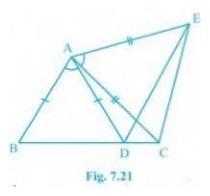

Answer
It is given in the question that \( \mathrm{AB}=\mathrm{AD},
\mathrm{AC}=\mathrm{AE} \), and \( \angle \mathrm{BAD}=\angle
\mathrm{EAC} \)To prove:
The line segment BC and DE are similar i.e. \( \mathrm{BC}=\mathrm{DE} \)
Proof:
We know that \( \mathrm{BAD}=\mathrm{EAC} \)
Now, by adding DAC on both sides we get,
\( \mathrm{BAD}+\mathrm{DAC}=\mathrm{EAC}+\mathrm{DAC} \)
This implies, \( \mathrm{BAC}=\mathrm{EAD} \)
Now, \( \triangle \mathrm{ABC} \) and \( \triangle \mathrm{ADE} \) are similar by SAS congruency since:
(i) \( \mathrm{AC}=\mathrm{AE} \quad\) (As given in the question)
(ii) \( \mathrm{BAC}=\mathrm{EAD} \)
(iii) \( \mathrm{AB}=\mathrm{AD} \quad\) (It is also given in the question)
\( \therefore \) Triangles ABC and ADE are similar i.e. \( \triangle \mathrm{ABC} \triangle \mathrm{ADE} \).
So, by the rule of CPCT, it can be said that \( \mathrm{BC}=\mathrm{DE} \).
7. \( A B \) is a line segment and \( P \) is its mid-point. \( D
\) and \( E \) are points on the same side of \( A B \) such that
\( B A D=A B E \) and \( E P A=D P B \) (see Fig. 7.22). Show
that
(i) \( \triangle DAP\) \( \triangle EBP\)
(ii) \( \mathrm{AD}=\mathrm{BE} \)
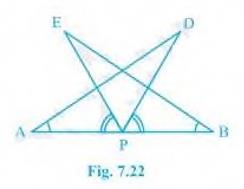
(i) \( \triangle DAP\) \( \triangle EBP\)
(ii) \( \mathrm{AD}=\mathrm{BE} \)

Answer
In the question, it is given that \( P \) is the mid-point of line
segment \( A B \). Also, \( \mathrm{BAD}=\mathrm{ABE} \) and \(
\mathrm{EPA}=\mathrm{DPB} \)(i) It is given that \(EPA = DPB\)
Now, add \(DPE\) on both sides,
\(\mathrm{EPA}+\mathrm{DPE}=\mathrm{DPB}+\mathrm{DPE}\)
This implies that angles \(DPA\) and \(EPB\) are equal i.e. \( \mathrm{DPA}=\mathrm{EPB} \)
Now, consider the triangles \(DAP\) and \(EBP\).
\(\mathrm{DPA} =\mathrm{EPB} \)
\( \mathrm{AP}=\mathrm{BP} \quad\) (Since P is the mid-point of the line segment AB\( ) \)
\( \mathrm{BAD}=\mathrm{ABE} \) (As given in the question)
So, by ASA congruency, \( \triangle \mathrm{DAP} \triangle \mathrm{EBP} \).
(ii) By the rule of \( \mathrm{CPCT}, \mathrm{AD}=\mathrm{BE} \).
8. In right triangle \(ABC\), right angled at \( C, M \) is the
mid-point of hypotenuse \( A B \). \( C \) is joined to \( M \)
and produced to a point \( D \) such that \(DM = CM\). Point \(D\)
is joined to point \(B\) (see Fig. 7.23). Show that:
(i) \( \triangle \mathrm{AMC} \triangle \mathrm{BMD} \)
(ii) DBC is a right angle.
(iii) \( \triangle \mathrm{DBC} \triangle \mathrm{ACB} \)
(iv) \( \mathrm{CM}=\frac{1}{2} \mathrm{AB} \)
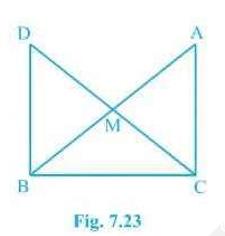
(i) \( \triangle \mathrm{AMC} \triangle \mathrm{BMD} \)
(ii) DBC is a right angle.
(iii) \( \triangle \mathrm{DBC} \triangle \mathrm{ACB} \)
(iv) \( \mathrm{CM}=\frac{1}{2} \mathrm{AB} \)

Answer
It is given that M is the mid-point of the line segment \( A B,
C=90^{\circ} \), and \( \mathrm{DM}=\mathrm{CM} \)(i) Consider the triangles \( \triangle \mathrm{AMC} \) and \( \triangle \mathrm{BMD} \) :
\( \mathrm{AM}=\mathrm{BM} \) (Since M is the mid-point)
\( \mathrm{CM}=\mathrm{DM} \) (Given in the question)
\( \mathrm{CMA}=\mathrm{DMB} \) (They are vertically opposite angles)
So, by SAS congruency criterion, \( \triangle \mathrm{AMC} \triangle \mathrm{BMD} \).
(ii) \( \mathrm{ACM}=\mathrm{BDM} \) (by CPCT)
\( \therefore \mathrm{AC} \mathrm{BD} \) as alternate interior angles are equal.
Now, \( \mathrm{ACB}+\mathrm{DBC}=180^{\circ} \) (Since they are co-interiors angles)
\(\Rightarrow 90^{\circ}+\mathrm{B}=180^{\circ}\)
\(\therefore \mathrm{DBC}=90^{\circ}\)
(iii) In \( \triangle \mathrm{DBC} \) and \( \triangle \mathrm{ACB} \),
\(\mathrm{BC} =\mathrm{CB}\quad\) (Common side)
\(\mathrm{ACB} =\mathrm{DBC}\quad\) (They are right angles)
\(\mathrm{DB} =\mathrm{AC}\quad\) (by CPCT)
So, \( \triangle \mathrm{DBC} \triangle \mathrm{ACB} \) by SAS congruency.
(iv) \( \mathrm{DC}=\mathrm{AB} \quad\) (Since \( \triangle \mathrm{DBC} \triangle \mathrm{ACB} \) )
\( \Rightarrow \mathrm{DM}=\mathrm{CM}=\mathrm{AM}=\mathrm{BM} \) (Since M the is mid-point)
So, \( \mathrm{DM}+\mathrm{CM}=\mathrm{BM}+\mathrm{AM} \)
Hence, \( \mathrm{CM}+\mathrm{CM}=\mathrm{AB} \)
\(\Rightarrow \mathrm{CM}=\left(\frac{1}{2}\right) \mathrm{AB}\)

