CBSE Class 10 Maths Chapter 2 Polynomials solutions Ex 2.3 Math Solution || NCERT Solutions for Class 10 Maths Chapter 2: Polynomials (English Medium)
Explore the NCERT Solutions for Class 10 Maths Chapter 2: Polynomials (English Medium), with detailed explanations for Exercise 2.3. This resource is designed to simplify complex polynomial concepts, helping Class 10 Maths students grasp the subject effortlessly. For any queries regarding NCERT Solutions for Class 10 Maths Chapter 2 Polynomials Ex 2.3, feel free to leave a comment, and we’ll respond as soon as possible. ||
Class 10 Maths Chapter 2 Polynomials solutions Ex 2.3 || NCERT Solutions for Class 10 Maths Chapter 2: Polynomials (English Medium)

CBSE Class 10 Maths Chapter 2 Polynomials solutions Ex 2.3 Math Solution || NCERT Solutions for Class 10 Maths Chapter 2: Polynomials (English Medium)
Exercise-2.3
1. Divide the polynomial by the polynomial and find the quotient and remainder in each of the following:
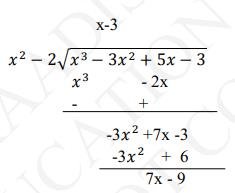
Quotient \( =x-3 \)
Remainder \( =7 x-9 \)
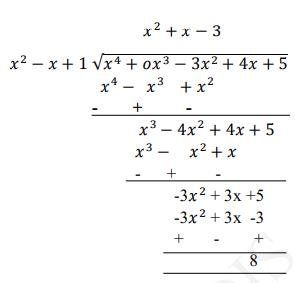
Quotient \( =x^{2}+x-3 \)
Remainder \( =8 \)
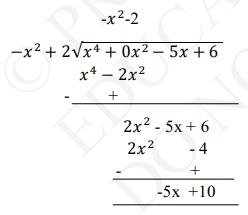
Quotient \( =-x^{2}-2 \)
Remainder \( =-5 x+10 \)
2. Check whether the first polynomial is a factor of the second polynomial by dividing the second polynomial by the first polynomial :
CBSE Class 10 Maths Chapter 2 Polynomials solutions Ex 2.3 Math Solution || NCERT Solutions for Class 10 Maths Chapter 2: Polynomials (English Medium)

Since the remainder is 0 ,
Hence, \( t^{2}-3 \) is a factor of \( 2 t^{4}+3 t^{3}-2 t^{2}-9 t-12 \).
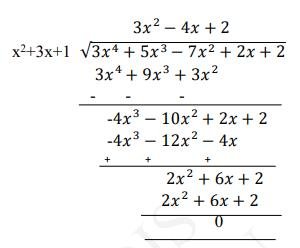
Since the remainder is 0 ,
Hence, \( x^{2}+3 x+1 \) is a factor of \( 3 x^{4}+5 x^{3}-7 x^{2}+2 x+2 \).

Since the remainder \( \neq 0 \),
Hence, \( x^{3}-3 x+1 \) is not a factor of \( x^{5}-4 x^{3}+x^{2}+3x+1 \).
if two of its zeroes are \( \sqrt{\frac{5}{3}} \) and \( -\sqrt{\frac{5}{3}} \).
Since the two zeroes are \( \sqrt{\frac{5}{3}} \) and \( -\sqrt{\frac{5}{3}} \)
\( \therefore\left(x-\sqrt{\frac{5}{3}}\right)\left(x+\sqrt{\frac{5}{3}}\right)=\left(x^{2}-\frac{5}{3}\right) \) is a factor of \( 3 x^{4}+6 x^{3}-2 x^{2}-10 x-5 \).
Therefore, we divide the given polynomial by \( x^{2}-\frac{5}{3} \).

We know, Dividend \( =( \)Divisor \( \times \) quotient\( )+ \) remainder
\(3 x^{4}+6 x^{3}-2 x^{2}-10 x-5=\left(x^{2}-\frac{5}{3}\right)\left(3 x^{2}+6 x+3\right)\)
\( 3 x^{4}+6 x^{3}-2 x^{2}-10 x-5=\left(x^{2}-\frac{5}{3}\right)\left(x^{2}+2 x+1\right) \)
As \( (a+b)^{2}=a^{2}+b^{2}+2 a b \)
So, \( x^{2}+2 x+1=(x+1)^{2} \)
\( 3 x^{4}+6 x^{3}-2 x^{2}-10 x-5=3\left(x^{2}-\frac{5}{3}\right)(x+1)^{2} \) Therefore, its zero is given by \( x+1=0 \).
\( \Rightarrow x=-1,-1 \)
Hence, the zeroes of the given polynomial are \( \sqrt{\frac{5}{3}} \) and \( -\sqrt{\frac{5}{3}} \). and \(-1 , -1\) .
CBSE Class 10 Maths Chapter 2 Polynomials solutions Ex 2.3 Math Solution || NCERT Solutions for Class 10 Maths Chapter 2: Polynomials (English Medium)
Polynomial, \( \mathrm{p}(x)=x^{3}-3 x^{2}+x+2 \) (dividend)
Quotient \( =(x-2) \)
Remainder \( =(-2 x+4) \)
To find: divisor \( =\mathrm{g}(x) \) we know, Dividend \( = \) Divisor \( \times \) Quotient + Remainder
\(\Rightarrow x^{3}-3 x^{2}+x+2=g(x) \times(x-2)+(-2 x+4)\)
\(\Rightarrow x^{3}-3 x^{2}+x+2+2 x-4=g(x)(x-2)\)
\(\Rightarrow x^{3}-3 x^{2}+3 x-2=g(x)(x-2)\)
\( \mathrm{g}(x) \) is the quotient when we divide \( \left(x^{3}-3 x^{2}+3 x-2\right) \) by \( (x-2) \)
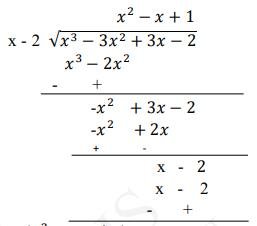
\( \therefore \mathrm{g}(x)=\left(x^{2}-x+1\right) \)
5.
By division Algorithm : \( \mathrm{p}(x)=\mathrm{g}(x) \ x \ \mathrm{q}(x)+\mathrm{r}
(x) \)
It means when \( P(x) \) is divided by \( g(x) \) then quotient is \( q(x) \) and remainder is \( r(x) \) We need to start with \( p(x)=q(x) \) This means that the degree of polynomial \( \mathrm{p}(x) \) and quotient \( \mathrm{q}(x) \) is
same. This can only happen if the degree of \( g(x)=0 \) i.e \( p(x) \) is divided by a constant. Let \( p(x)=x^{2}+1 \) and \( g(x)=2 \)
\(\frac{p(x)}{g(x)}=\frac{x^{2}+1}{2}\)
The,
\(p(x)=g(x) \times\left(\frac{x^{2}+1}{2}\right)\)
Clearly, Degree of \( \mathrm{p}(x)= \) Degree of \(
\mathrm{q}(x) \)
2. Checking for division algorithm,
\(p(x)=g(x) \times q(x)+r(x)\)
\(=6 x^{2}+2 x+2=3\left(3 x^{2}+x+1\right)\)
\(=6 x^{2}+2 x+2\)
Thus, the division algorithm is satisfied.
Let us assume the division of \( x^{3}+x \) by \( x^{2} \),
Here,
\(\mathrm{p}(x)=x^{3}+x\)
\(\mathrm{g}(x)=x^{2}\)
\(\mathrm{q}(x)=x \text { and } \mathrm{r}(x)=x\)
Clearly, the degree of \( q(x) \) and \( r(x) \) is the same i.e.,
Checking for division algorithm,
\(\mathrm{p}(x)=\mathrm{g}(x) \times
\mathrm{q}(x)+\mathrm{r}(x) x^{3}+x\)
\(=\left(x^{2}\right) \times x+x \)
\(=x^{3}+x=x^{3}+x\)
Thus, the division algorithm is satisfied.
Degree of the remainder will be 0 when the remainder comes to a constant.
Let us assume the division of \( x^{3}+1 \) by \( x^{2} \).
Here,
\(p(x)=x^{3}+1 g(x)=x^{2}\)
\(q(x)=x \text { and } r(x)=1\)
Clearly, the degree of \( r(x) \) is 0 . Checking for division algorithm,
\(p(x)=g(x) \times q(x)+r(x) x^{3}+1\)
\(=\left(x^{2}\right) \times x+1 \ x^{3}+1=x^{3}+1\)
Thus, the division algorithm is satisfied.
CBSE Class 10 Maths Chapter 2 Polynomials solutions Ex 2.3 Math Solution || NCERT Solutions for Class 10 Maths Chapter 2: Polynomials (English Medium)
Class 10 : NCERT Solutions for Class 10 Maths Chapter 1 Exercise 1.1
Class 10 : NCERT Solutions for Class 10 Maths Chapter 1 Exercise 1.2
Class 10 : NCERT Solutions for Class 10 Maths Chapter 1 Exercise 1.3
Class 10 : CBSE Class 10 Maths Chapter 2 Polynomials Ex 2.1
Class 10 : CBSE Class 10 Maths Chapter 5 Arithmetic Progressions Ex 5.3
Class 10 : NCERT Solutions for Class 10 Maths Chapter 8 Exercise 8.2
Class 10 : CBSE Class 10 Maths Chapter 10 Circles solutions Ex 10.2
Class 10 : CBSE Class 10 Maths Chapter 13 Surface Areas and Volumes solutions Ex 13.2
Class 10 : CBSE Class 10 Maths Chapter 13 Surface Areas and Volumes solutions Ex 13.3
