NCERT Solutions for Class 10 Maths Chapter 13: Surface Areas and Volumes || CBSE Class 10 Maths Chapter 13 Surface Areas and Volumes solutions Ex 13.2
Discover the complete NCERT Solutions for Class 10 Maths Chapter 13 Surface Areas and Volumes solutions (English Medium), with step-by-step explanations for Exercise 13.2. This resource ensures a thorough understanding of Surface Areas and Volumes, helping Class 10 Maths students excel in their exams. If you have any queries regarding the NCERT Solutions for Class 10 Maths Chapter 13 Surface Areas and Volumes solutions Ex 13.2, drop a comment below, and we’ll assist you at the earliest. NCERT Solutions for Class 10 Maths Chapter 13: Surface Areas and Volumes. Class 10 Maths Chapter 13 Surface Areas and Volumes solutions Ex 13.2

NCERT Solutions for Class 10 Maths Chapter 13: Surface Areas and Volumes || CBSE Class 10 Maths Chapter 13 Surface Areas and Volumes solutions Ex 13.2
Exercise-13.2
NCERT Solutions for Class 10 Maths Chapter 13: Surface Areas and Volumes || CBSE Class 10 Maths Chapter 13 Surface Areas and Volumes solutions Ex 13.2
Download the Math Ninja App Now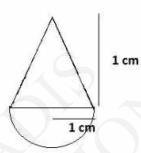
Given:
Height (h) of conical part \( = \) Radius (r) of conical part \( =1 \mathrm{~cm} \)
Radius (r) of hemispherical part \( = \) Radius of conical part \( (\mathrm{r})=1 \mathrm{~cm} \)
Volume of solid \(=\) Volume of conical part \(+\) Volume of hemispherical part
\(=\frac{1}{3} \pi r^{2} \mathrm{h}+\frac{2}{3} \pi \mathrm{r}^{3}\)
\(=\frac{1}{3} \pi(1)^{2}(1)+\frac{2 \pi}{3}(1)^{3}\)
\(=\frac{\pi}{3}+\frac{2 \pi}{3}\)
\(=\frac{3 \pi}{3}\)
\(=\pi \mathrm{cm}^{3}\)
Hence, Volume of the solid \( =\pi \mathrm{cm}^{3} \)
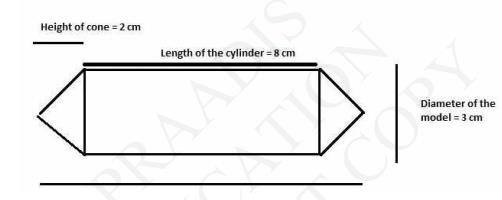
Height \( \left(\mathrm{h}^{1}\right) \) of each conical part \( =2 \mathrm{~cm} \)
Height \( \left(\mathrm{h}^{2}\right) \) of cylindrical part \( =1^{2}-2 \times \) Height of conical part \( =1^{2}-2 \times 2=8 \mathrm{~cm} \)
Radius \( = \text{Diameter}/ 2\)
Radius (r) of cylindrical part \( =\frac{3}{2} \mathrm{~cm} \)
Radius of conical part \( =\frac{3}{2} \mathrm{~cm} \)
Volume of air present in the model \( = \) Volume of cylinder \( +2 \times \) Volume of cones
volume of cylinder \( =\frac{1}{3} \pi \mathrm{r}^{2} \mathrm{~h} \)
Volume of air present in the model \( =\pi \mathrm{r}^{2} \mathrm{~h}^{2}+2 \times \frac{1}{3} \pi \mathrm{r}^{2} \mathrm{~h}^{1} \)
Volume of air present in the model
\( =\pi\left(\frac{3}{2}\right)^{2}(8) 2 \times \frac{1}{3} \pi\left(\frac{3}{2}\right)^{2}(2) \)
\(=18 \pi+3 \pi\)
\(=21 \pi\)
\(=21 \times \frac{ 22 }{ 7 }\)
\(=3 \times 22\)
\(=66 \mathrm{~cm}^{3}\)
Hence, volume of air contained in the model that Rachel made \( =66 \mathrm{~cm}^{3}\)
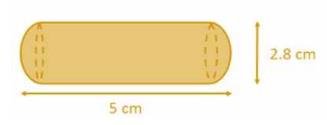
Radius (r) of cylindrical part \( =\frac{2.8}{2}=1.4 \mathrm{~cm} \)
Radius \( (\mathrm{R}) \) of hemispherical part \( =\frac{2.8}{2}=1.4 \mathrm{~cm} \)
Length of each hemispherical part \( =1.4 \mathrm{~cm} \)
The radius of hemispherical part \( =1.4 \mathrm{~cm} \)
Length (h) of cylindrical part \( =5-2 \times \) Length of hemispherical part
\(=5-(2 \times 1.4)\)
\(=5-2.8\)
\(=2.2 \mathrm{~cm}\)
The volume of one gulabjamun \( = \) Vol. of cylindrical part \( +2 \times \) Vol. of hemispherical part
\(=\left(\pi \mathrm{r}^{2} \mathrm{~h}\right)+\left(2 \times \frac{2}{3} \pi \mathrm{R}^{3}\right)\)
\(=\left(\pi \mathrm{r}^{2} \mathrm{~h}\right)+\left(\frac{4}{3} \pi \mathrm{R}^{3}\right)\)
\(=\left[\pi \times(1.4)^{2} \times 2.2\right]+\left[\frac{4}{3} \pi(1.4)^{3}\right]\)
\(=\left(\frac{22}{7} \times 1.4 \times 1.4 \times 2.2\right)+\left(\frac{4}{3} \times \frac{22}{7} \times 1.4 \times 1.4 \times 1.4\right)\)
\(=\left(\frac{94.864}{7}\right)+\left(\frac{241.472}{21}\right)\)
\(=13.552+11.498\)
\(=25.05 \mathrm{~cm}^{3}\)
Volume of 45 gulabjamun \( =45 \times 25.05 \)
\(=1,127.25 \mathrm{~cm}^{3}\)
The volume of sugar syrup \( =30 \% \) of the volume
\(=\frac{30}{100} \times 1127.25\)
\(=338.17 \mathrm{~cm}^{3}\)
\(=338 \mathrm{~cm}^{3} \text { (approx.) }\)
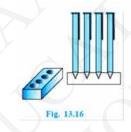
Depth (h) of each conical depression \( =1.4 \mathrm{~cm} \)
Radius (r) of each conical depression \( =0.5 \mathrm{~cm} \)
Volume of wood \( = \) Volume of cuboid \( -4 \times \) Volume of cones
\(= \mathrm{lbh}-4 \times \frac{1}{3} \pi \mathrm{r}^{2} \mathrm{~h}\)
\(=15 \times 10 \times 3.5-4 \times \frac{1}{3} \times \frac{22}{7} \times\left(\frac{1}{2}\right)^{2} \times 1.4\)
\(=525-1.47\)
\( =523.53 \mathrm{~cm}^{3} \)
Hence,
The volume of wood in the entire stand \( =523.53 \mathrm{~cm}^{3} \)
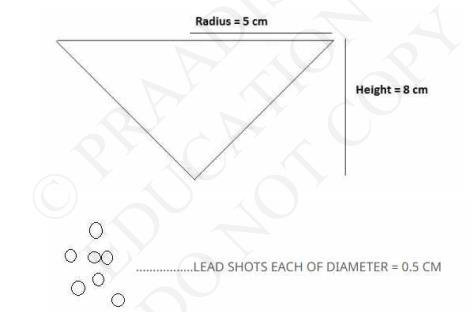
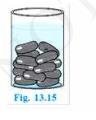
When lead shots are dropped in the Vessel, the same amount of water will come out of the vessel as the Total Volume of Lead Shots.
Height (h) of conical vessel \( =8 \mathrm{~cm} \)
Radius (\( \mathrm{r}_{1} \)) of conical vessel \( =5 \mathrm{~cm} \)
Radius (\( \mathrm{r}_{2} \)) of lead shots \( =0.5 \mathrm{~cm} \)
Volume of water \( = \) Volume of Vessel Let n number of lead shots were dropped in the vessel
Volume of water spilled = Volume of dropped lead shots
Volume of vessel \( =\frac{1}{3} \pi r_{1}^{2} \mathrm{~h} \)
Volume of vessel \( =\frac{1}{3} \pi(5)^{2} 8 \)
Volume of water spilled \( =\frac{1}{4} \times \) volume of vessel
Volume of water spilled \( =\frac{1}{12} \pi \times 25 \times 8 \)
Volume of lead shots \( =\mathrm{n} \times \frac{4}{3} \pi r_{2}^{3} \)
Volume of lead shots \( =\mathrm{n} \times \frac{4}{3} \pi(0.5)^{3} \)
Volume of lead shots \( = \) Volume of water spilled
\( \mathrm{n} \times \frac{4}{3} \pi(0.5)^{3}=\frac{1}{12} \pi \times 25 \times 8 \)
\( \mathrm{n}=\frac{25 \times 8 \times 3}{12 \times 4 \times 0.5 \times 0.5 \times 0.5} \)
\( \mathrm{n}=100 \)
Hence, the number of lead shots dropped in the vessel is 100.
NCERT Solutions for Class 10 Maths Chapter 13: Surface Areas and Volumes || CBSE Class 10 Maths Chapter 13 Surface Areas and Volumes solutions Ex 13.2
Download the Math Ninja App Now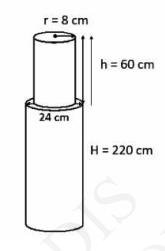
Given:
Height (H) of larger cylinder \( =220 \mathrm{~cm} \)
Radius (R) of larger cylinder \( =\frac{24}{2}=12 \mathrm{~cm} \)
Height (h) of smaller cylinder \( =60 \mathrm{~cm} \)
Radius (r) of smaller cylinder \( =8 \mathrm{~cm} \)
Total volume \( = \) Volume \( ( \)Larger cylinder\( ) \ + \) Volume \( ( \)Smaller cylinder\( ) \)
\(=\pi(\mathrm{R})^{2} \mathrm{H}+\pi(\mathrm{r})^{2} \mathrm{~h}\)
\(=\pi(12)^{2} \times 220+\pi(8)^{2} \times 60\)
\(=\pi[(144 \times 220)+(64 \times 60)]\)
\(=\pi[31680+3840]\)
\(=35520 \times 3.14\)
\(=111532.8 \mathrm{~cm}^{3}\)
Mass of \( 1 \mathrm{~cm}^{3} \) iron \( =8 \mathrm{~g} \)
Mass of \( 111532.8 \mathrm{~cm}^{3} \) iron \( =111532.8 \times 8 \)
\( =892262.4 \mathrm{~g} \)
\( =892.262 \mathrm{~kg} \)
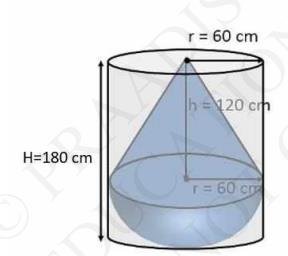
Radius (r) of hemispherical part \( = \) Radius (r) of conical part \( =60 \mathrm{~cm} \)
Height (h) of conical part of solid \( =120 \mathrm{~cm} \)
Height (H) of cylinder \( =180 \mathrm{~cm} \)
Radius (r) of cylinder \( =60 \mathrm{~cm} \)
Volume of water left \( = \) Volume of cylinder \(-\) Volume of solid
\( = \) Volume of cylinder \( - \ ( \)Volume of cone \(+\) Volume of hemisphere\( ) \)
\( =\pi \mathrm{r}^{2} \mathrm{H}-\left(\frac{1}{3} \pi \mathrm{r}^{2} \mathrm{~h}+\frac{2}{3} \pi \mathrm{r}^{3}\right) \)
\(=\left[\pi(60)^{2}(180)\right]-\left[\frac{1}{3} \pi(60)^{2} \times 120+\frac{2}{3} \pi(60)^{3}\right]\)
\(=648000 \pi-(144000 \pi+144000 \pi)\)
\(=648000 \pi-288000 \pi\)
\(=360000 \pi\)
\(=1131428.57 \mathrm{~cm}^{3}\)
\(=1.131 \mathrm{~m}^{3} \text { (approx.) }\)
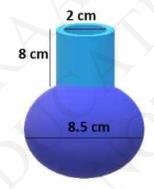
Given:
Height (h) of cylindrical part \( =8 \mathrm{~cm} \)
Radius \( (\mathrm{r}_{2} ) \) of cylindrical part \( =\frac{2}{2}=1 \mathrm{~cm} \)
Radius \( \left(\mathrm{r}_{1}\right) \) spherical part \( =\frac{8.5}{2}=4.25 \mathrm{~cm} \)
Volume of vessel \( = \) Volume of sphere \(+\) Volume of cylinder
\(=\frac{4}{3} \pi\left(r_{1}\right)^{3}+\pi\left(r_{2}\right)^{2} \mathrm{~h}\)
\(=\frac{4}{3} \pi(4.25)^{3}+\pi(1)^{2}(8)\)
\(=\left(\frac{4}{3} \times 3.14 \times 76.765625\right)+(8 \times 3.14)\)
\(=321.392+25.12\)
\(=346.512\)
\(=346.51 \mathrm{~cm}^{3}\)
Hence,
From the result we can conclude that she is wrong.
NCERT Solutions for Class 10 Maths Chapter 13: Surface Areas and Volumes || CBSE Class 10 Maths Chapter 13 Surface Areas and Volumes solutions Ex 13.2
Download the Math Ninja App NowClass 10 : NCERT Solutions for Class 10 Maths Chapter 1 Exercise 1.1
Class 10 : NCERT Solutions for Class 10 Maths Chapter 1 Exercise 1.2
Class 10 : CBSE Class 10 Maths Chapter 2 Polynomials Ex 2.1 || NCERT Solutions for Class 10 Maths Chapter 2: Polynomials (English Medium)
Class 10 : CBSE Class 10 Maths Chapter 10 Circles solutions Ex 10.2
Class 10 : CBSE Class 10 Maths Chapter 13 Surface Areas and Volumes solutions Ex 13.3