Ch 8 Miscellaneous Exercise Class 12​

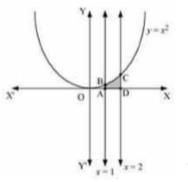
We can see from the figure that the area of the region bounded by the curve \( y=x^{2} \) and the lines \( x=1, x=2 \) is shown by shaded region that is Area ADCBA.
Area of \( \mathrm{ADCBA}=\int_{1}^{2} y d y=\int_{1}^{2} x^{2} d x \)
\( \Rightarrow=\left[\frac{x^{3}}{3}\right]_{1}^{2} \)
\( \Rightarrow=\frac{8}{3}-\frac{1}{3} \)
\( \Rightarrow=\frac{7}{3} \) units

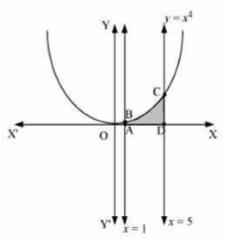
We can see from the figure that the area of the region bounded by the curve \( y=x^{4} \) and the lines \( x=1, x=5 \) is shown by shaded region that is Area ADCBA.
Area of \( \mathrm{ADCBA}=\int_{1}^{5} y d y=\int_{1}^{5} x^{4} d x \)
\(\Rightarrow=\left[\frac{x^{5}}{3}\right]_{1}^{5}\)
\(\Rightarrow=625-\frac{1}{5}\)
\(=624.8 \text { units. }\)

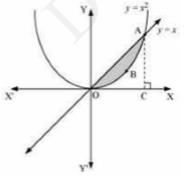
We can see from the figure that the area of the region bounded by the curve \( y=x \) and \( y=x^{2} \) and points of intersection are \( A(1,1) \).
Thus,
Area of \( \mathrm{OBAO}=\operatorname{Area}(\triangle \mathrm{OCA})- \) Area \( (\mathrm{OCABO}) \)
\( \Rightarrow=\int_{0}^{1} x d x-\int_{0}^{1} x^{2} d x \)
\( \Rightarrow=\left[\frac{x^{2}}{2}\right]_{0}^{1}-\left[\frac{x^{3}}{3}\right]_{0}^{1} \)
\( \Rightarrow=\frac{1}{2}-\frac{1}{3} \)
\( \Rightarrow=\frac{1}{6} \) units

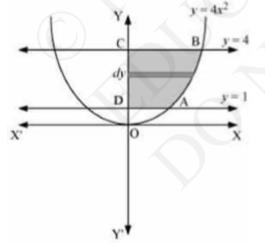
We can see from the figure that the area of the region bounded by the curve \( y=4 x^{2} \) and the lines \( y=1 \) and \( y=4 \) is shown by shaded region that is Area ABCDA .
Area of \( \mathrm{ABCDA}=\int_{1}^{4} x d y=\int_{1}^{4} \frac{\sqrt{y}}{2} d y \)
\(\Rightarrow=\frac{1}{2} \int_{1}^{4} \sqrt{y} d y\)
\(\Rightarrow=\frac{1}{2} \times \frac{2}{3}\left[y^{\frac{3}{2}}\right]_{1}^{4}\)
\(\Rightarrow=\frac{1}{2}\left[(4)^{\frac{3}{2}}-(1)^{\frac{3}{2}}\right]\)
\(\Rightarrow=\frac{1}{3}(8-1)\)
\(\Rightarrow=\frac{7}{3} \text { units }\)

It is given that \( y=|x+3| \)
The value of x and y are given in the following table:
\(\begin{array}{|l|l|l|l|l|l|l|l|}
\hline X & -6 & -5 & -4 & -3 & -2 & -1 & 0 \\
\hline Y & 3 & 2 & 1 & 0 & 1 & 2 & 3 \\
\hline
\end{array}\)
By plotting these points, we get the graph of \( y=|x+3| \) as below:

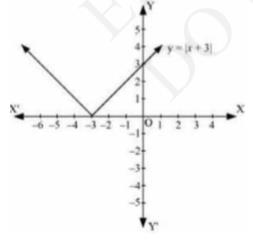
\( \text{We know that,} (x+3) \leq 0 \) \( \text{for } -6 \leq x \leq-3 \) and \( (x+3) \geq 0 \) for \( -3 \leq x \leq 0 \)
Thus, \( \int_{-6}^{0}|x+3| d x=-\int_{-6}^{-3}(x+3) d x+\int_{-3}^{0}(x+3) d x \)
\(\Rightarrow=-\left[\frac{x^{2}}{2}+3 x\right]_{-6}^{-3}+\left[\frac{x^{2}}{2}+3 x\right]_{-3}^{0}\)
\(\Rightarrow=-\left[\left(\frac{(-3)^{2}}{2}+3(-3)\right)\left(\frac{(-6)^{2}}{2}+3(-6)\right)\right]+\left[0-\left(\frac{(-3)^{2}}{2}+3(-3)\right)\right]\)
\(\Rightarrow=-\left[-\frac{9}{2}\right]-\left[-\frac{9}{2}\right]\)
\(=9\)

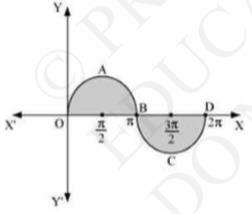
The required area \( = \) Area of \( \mathrm{OABO}+ \) Area BCDB
\(\Rightarrow=\int_{0}^{\pi} \sin x d x+\left|\int_{\pi}^{2 \pi} \sin x d x\right|\)
\(\Rightarrow=[-\cos x]_{0}^{\pi}+\left|[-\cos x]_{0}^{2 \pi}\right|\)
\(=[-\cos \pi+\cos 0]+|-\cos 2 \pi+\cos \pi|\)
\(=1+1+|(-1-1)|\)
\(=2+|-2|\)
\(=2+2\)
\(=4 \text { units }\)

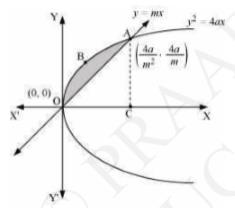
We can see from the figure that the area of the region bounded by the curve \( y^{2}=4 a x \) and the line \( y=m x \) is shown by shaded region that is Area OABO.
The points of intersection of both the curves are \( (0,0) \) and \( \left(\frac{4 a}{m^{2}}, \frac{4 a}{m}\right) \)
Now draw AC perpendicular to \( x- \)axis.
Thus,
Area of \( \mathrm{OABO}= \) Area \( \mathrm{OCABO}-\operatorname{Area}(\triangle \mathrm{OCA}) \)
\(\Rightarrow=\int_{0}^{\frac{4 a}{m^{2}}} 2 \sqrt{a} x d x-\int_{0}^{\frac{4 a}{m^{2}}} m x d x\)
\(\Rightarrow=2 \sqrt{a}\left[\frac{x^{\frac{3}{2}}}{\frac{3}{2}}\right]_{0}^{\frac{4 a}{m^{2}}}-m\left[\frac{x^{2}}{2}\right]_{0}^{\frac{4 a}{m^{2}}}\)
\(\Rightarrow=\frac{4}{3} \sqrt{a}\left(\frac{4 a}{m^{2}}\right)^{\frac{3}{2}}-\frac{m}{2}\left(\frac{4 a}{m^{2}}\right)^{2}\)
\(\Rightarrow=\frac{32 a^{2}}{3 m^{3}}-\frac{m}{2}\left(\frac{16 a^{2}}{m^{4}}\right)\)
\(\Rightarrow=\frac{32 a^{2}}{3 m^{3}}-\frac{8 a^{2}}{m^{3}}\)
\(\Rightarrow=\frac{8 a^{2}}{m^{3}} \text { units }\)

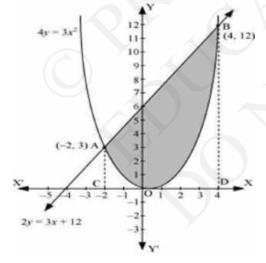
We can see from the figure that the area of the region bounded by the curve \( 4 y=3 x^{2} \) and the line \( 2 y=3 x+12 \) is shown by shaded region that is Area OBAO.
The points of intersection of both the curves are A \( (-2,3) \) and \( (4,12) \).
Now draw AC and BD perpendicular to \( x-\) axis.
Thus,
Area of OBAO \( = \) Area CDBA \( -( \) Area ODBA + Area OACO \( ) \)
\(\Rightarrow=\int_{-2}^{1} \frac{1}{2}(3 x+12) d x-\int_{-1}^{1} \frac{3 x^{2}}{4} d x\)
\(\Rightarrow=\frac{1}{2}\left[\frac{3 x^{2}}{2}+12 x\right]_{-2}^{4}-\frac{3}{4}\left[\frac{x^{3}}{3}\right]_{-2}^{4}\)
\(\Rightarrow=\frac{1}{2}[24+48-6+24]-\frac{1}{4}[64+8]\)
\(\Rightarrow=\frac{1}{2}[90]-\frac{1}{4}[72]\)
\(=45-18\)
\(=27 \text { units. }\)

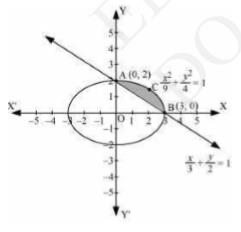
The area of the smaller region bounded by the ellipse is \( \frac{x^{2}}{9}+\frac{y^{2}}{4}=1 \) and the line \( \frac{x}{3}+\frac{y}{2}=1 \)
Area of \( \mathrm{BCAB}= \) Area \( \mathrm{OBCAO}- \) Area OBAO
\(\Rightarrow=\int_{0}^{3} 2 \sqrt{1-\frac{x^{2}}{9}} d x-\int_{0}^{3} 2\left(1-\frac{x}{3}\right) d x\)
\(\Rightarrow=\frac{2}{3}\left[\int_{0}^{3} \sqrt{9-x^{2}} d x\right]-\frac{2}{3} \int_{0}^{3}(3-x) d x\)
\(\Rightarrow=\frac{2}{3}\left[\frac{x}{2} \sqrt{9-x^{2}}+\frac{9}{2} \sin ^{-1} \frac{x}{3}\right]_{0}^{3}-\frac{2}{3}\left[3 x-\frac{x^{2}}{2}\right]_{0}^{3}\)
\(\Rightarrow=\frac{2}{3}\left[\frac{9}{2}\left(\frac{\pi}{2}\right)\right]-\frac{2}{3}\left[9-\frac{9}{2}\right]\)
\(\Rightarrow=\frac{2}{3} \times \frac{9}{4}[\pi-2]\)
\(\Rightarrow=\frac{3}{2}(\pi-2) \text { units }\)

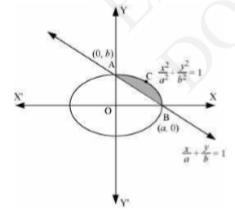
The area of the smaller region bounded by the ellipse is \( \frac{x^{2}}{9}+\frac{y^{2}}{4}=1 \) and the line \( \frac{x}{3}+\frac{y}{2}=1 \) Area of \( \mathrm{BCAB}= \) Area OBCAO - Area OBAO
\(\Rightarrow=\int_{b}^{a} b \sqrt{1-\frac{x^{2}}{a^{2}}} d x-\int_{b}^{a} b\left(1-\frac{x}{a}\right) d x\)
\(\Rightarrow=\frac{b}{a}\left[\int_{b}^{a} \sqrt{a^{2}-x^{2}} d x\right]-\frac{b}{a} \int_{b}^{a}(a-x) d x\)
\(\Rightarrow=\frac{b}{a}\left[\frac{x}{2} \sqrt{a^{2}-x^{2}}+\frac{a^{2}}{2} \sin ^{-1} \frac{x}{a}\right]_{0}^{a}-\left[a x-\frac{x^{2}}{2}\right]_{0}^{a}\)
\(\Rightarrow=\frac{b}{a}\left[\frac{a^{2}}{2}\left(\frac{\pi}{2}\right)\right]-\left[a^{2}-\frac{a^{2}}{2}\right]\)
\(\Rightarrow=\frac{b a^{2}}{2 a}\left[\frac{\pi}{2}-1\right]\)
\(\Rightarrow=\frac{a b}{4}[\pi-2] \text { units }\)

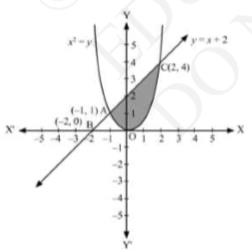
We can see from the figure that the area of the region bounded by the parabola \( x^{2}=y \), the line \( y=x+2 \) and the \( x \)-axis is shown by shaded region that is Area OACO.
The points of intersection of both the curves are \( A(-1,1) \) and \( C(2,4) \).
Thus,
Area of OACO
\(\Rightarrow=\int_{-1}^{2}(x+2) d x-\int_{-1}^{2} x^{2} d x\)
\(\Rightarrow=\left[\frac{x^{2}}{2}+2 x\right]_{-1}^{2}-\frac{1}{3}\left[x^{3}\right]_{-1}^{2}\)
\(\Rightarrow=\left[\left\{\frac{(2)^{2}}{2}+2(2)\right\}-\left\{\frac{(-1)^{2}}{2}+2(-1)\right\}\right]-\frac{1}{3}\left[(2)^{3}-(-1)^{3}\right]\)
\(\Rightarrow=\left[2+4-\left\{\frac{1}{2}-2\right\}\right]-\frac{1}{3}[8-1]\)
\(\Rightarrow=\left[6+\frac{3}{2}-3\right]\)
\(\Rightarrow=\frac{9}{2} \text { units }\)

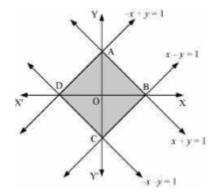
We can see from the figure that the area bounded by the curve \( |x|+|y|= \) 1 is shown by shaded region that is Area OACO.
\( \text{The curve intersects the axes at points} \ \mathrm{A}(0,1), \mathrm{B}(1,0), \mathrm{C}(0,-1) \) and \( \mathrm{D}(- \) 1,0 ).
We can observe that the given curve is symmetrical about x -axis and \( y- \)axis.
Thus,
Area \( \mathrm{ADCB}=4 \times \) Area OBAO
\(\Rightarrow=4 \int_{0}^{1}(1-x) d x\)
\(\Rightarrow=4\left[x-\frac{x^{2}}{2}\right]_{0}^{1}\)
\(\Rightarrow=4\left[1-\frac{1}{2}\right]\)
\(\Rightarrow=4\left(\frac{1}{2}\right)\)
\(=2 \text { units }\)

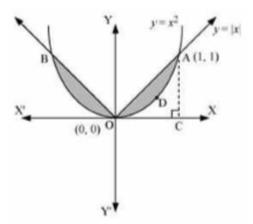
We can observe that the required area is symmetrical about \( y \)-axis.
Required area \( =2[ \) Area OCAO - Area OCADO]
\(\Rightarrow=2\left[\int_{0}^{1} x d x-\int_{0}^{1} x^{2} d x\right]\)
\(\Rightarrow=2\left[\left[\frac{x^{2}}{2}\right]_{0}^{1}-\left[\frac{x^{3}}{3}\right]_{0}^{1}\right]\)
\(\Rightarrow=2\left[\frac{1}{2}-\frac{1}{3}\right]\)
\(\Rightarrow=2\left(\frac{1}{6}\right)\)
\(\Rightarrow=\frac{1}{3}\)

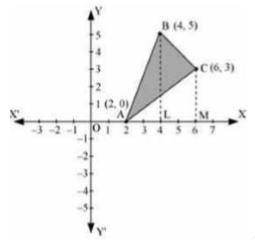
It is given that the vertices are \( \mathrm{A}(2,0), \mathrm{B}(4,5) \) and \( \mathrm{C}(6,3) \).
Now,
Equation of line segment \( A B \) is
\(\Rightarrow y-0=\frac{5-0}{4-0}(x-2)\)
\(\Rightarrow y-0=5 x-10\)
\(\Rightarrow y=\frac{5}{2}(x-2)\ldots(1)\)
Equation of line segment BC is
\(\Rightarrow y-5=\frac{3-5}{6-4}(x-4)\)
\(\Rightarrow 2 y-10=-2 x+8\)
\(\Rightarrow 2 y=-2 x+18\)
\(\Rightarrow y=-x+9\ldots(2)\)
Equation of line segment CA is
\(\Rightarrow y-3=\frac{0-3}{2-6}(x-6)\)
\(\Rightarrow-4 y+12=-3 x+18\)
\(\Rightarrow 4 y=3 x-6\)
\(y=\frac{3}{4}(x-2)\ldots(3)\)
Thus,
\(\text { Area }(\Delta \mathrm{ABC})=\text { Area ABLA }+ \text { Area BLMCA }- \text { Area ACMA }\)
\(\Rightarrow=\int_{2}^{4} \frac{5}{2}(x-2) d x+\int_{4}^{6}(-x+9) d x-\int_{4}^{6} \frac{3}{4}(x-2) d x\)
\(\Rightarrow=\frac{5}{2}\left[\frac{x^{2}}{2}-2 x\right]_{2}^{4}+\left[\frac{-x^{2}}{2}+9 x\right]_{4}^{6}-\frac{3}{4}\left[\frac{x^{2}}{2}-x=2 x\right]_{2}^{6}\)
\(\Rightarrow=\frac{5}{2}[8-8-2+4]+[-18+54+8-36]-\frac{3}{4}[18-12-2]\)
\(\Rightarrow=5+8-\frac{3}{4}(8)\)
\(=13-6\)
\(=7 \text { units }\)

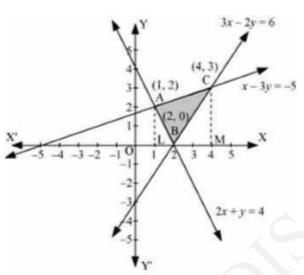
It is given lines if equations are \( 2 x+y=4,3 x-2 y=6 \) and \( x-3 y+5= \) 0 .
Thus, the area of the region bounded by the lines is the area of \( \triangle \mathrm{ABC} \).
And let us draw AL and CM perpendicular to \( x-\) axis.
Then,
\(\text { Area }(\triangle \mathrm{ABC})=\text { Area ALMCA }- \text { Area ALB - Area CMB }\)
\(\Rightarrow=\int_{1}^{4}\left(\frac{x+5}{3}\right) d x-\int_{1}^{2}(4-2) d x-\int_{2}^{4}\left(\frac{3 x-6}{2}\right) d x\)
\(\Rightarrow=\frac{1}{3}\left[\frac{x^{2}}{2}+5 x\right]_{1}^{4}-\left[-4-x^{2}\right]_{1}^{2}-\frac{1}{2}\left[\frac{3 x^{2}}{2}-6 x\right]_{2}^{4}\)
\(\Rightarrow=\frac{1}{3}\left[8+20-\frac{1}{2}-5\right]-[8-4-4+1]-\frac{1}{2}[24-24-6+12]\)
\(\Rightarrow=\left(\frac{1}{3} \times \frac{45}{2}\right)-(1)-\frac{1}{2}(6)\)
\(\Rightarrow=\frac{15}{2}-1-3\)
\(\Rightarrow=\frac{15}{2}-4\)
\(\Rightarrow=\frac{15-8}{2}\)
\(\Rightarrow=\frac{7}{2}\)

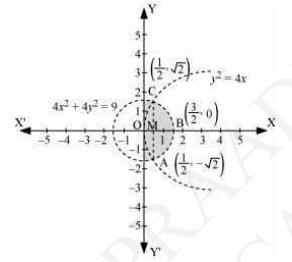
\( \text{The area bounded by the curves,} \left\{(x, y): y^{2} \leq 4 x, 4 x^{2}+4 y^{2} \leq 9\right\} \), is shown by shaded region as OABCO.
The points of intersection of both the curves are \( \left(\frac{1}{2}, \sqrt{2}\right) \) and \( \left(\frac{1}{2} .-\sqrt{2}\right) \)
We can observe that area OABCO is symmetrical about \( x\)-axis.
Thus, Area of \( \mathrm{OABCO}=2 \times \) Area OBC
Now,
Area \( \mathrm{OBCO}= \) Area \( \mathrm{OMC}+ \) Area MBC
\(\Rightarrow=\int_{0}^{\frac{1}{2}} 2 \sqrt{x} d x+\int_{\frac{1}{2}}^{\frac{3}{2}} \frac{1}{2} \sqrt{9-4 x^{2}} d x\)
\(\Rightarrow=\int_{0}^{\frac{1}{2}} 2 \sqrt{x} d x+\int_{\frac{1}{2}}^{\frac{3}{2}} \frac{1}{2} \sqrt{(3)^{2}-(2 x)^{2}} d x\)
Put \( 2 x=\mathrm{t} \)
\(\Rightarrow \mathrm{dx}=\frac{d t}{2}\)
So, when \( x=\frac{3}{2}, \mathrm{t}=3 \) and \( x=\frac{1}{2}, \mathrm{t}=1 \), we get,
\(\Rightarrow=\int_{0}^{\frac{1}{2}} 2 \sqrt{x} d x+\frac{1}{4} \int_{1}^{3} \sqrt{(3)^{2}-(t)^{2}} d t\)
\(\Rightarrow=2\left[\frac{x^{\frac{3}{2}}}{\frac{3}{2}}\right]_{0}^{\frac{1}{2}}+\frac{1}{4}\left[\frac{t}{2} \sqrt{9-t^{2}}+\frac{9}{2} \sin ^{-1}\left(\frac{t}{3}\right)\right]_{1}^{3}\)
\(\Rightarrow=2\left[\frac{2}{3}\left(\frac{1}{2}\right)^{\frac{3}{2}}\right]+\frac{1}{4}\left[\left\{\frac{3}{2} \sqrt{9-(3)^{2}}+\frac{9}{2} \sin ^{-1}\left(\frac{3}{3}\right)\right\}-\left\{\frac{1}{2} \sqrt{9-(1)^{2}}+\frac{9}{2} \sin ^{-1}\left(\frac{1}{3}\right)\right\}\right]\)
\(\Rightarrow=\frac{2}{3 \sqrt{2}}+\frac{1}{4}\left[\left\{0+\frac{9}{2} \sin ^{-1}(1)\right\}-\left\{\frac{1}{2} \sqrt{8}+\frac{9}{2} \sin ^{-1}\left(\frac{1}{3}\right)\right\}\right]\)
\(\Rightarrow=\frac{\sqrt{2}}{3}+\frac{1}{4}\left[\frac{9 \pi}{4}-\sqrt{2}-\frac{9}{2} \sin ^{-1}\left(\frac{1}{3}\right)\right]\)
\(\Rightarrow=\frac{\sqrt{2}}{3}+\frac{9 \pi}{16}-\frac{\sqrt{2}}{3}+\frac{9 \pi}{8} \sin ^{-1}\left(\frac{1}{3}\right)\)
\(\Rightarrow=\frac{9 \pi}{16}-\frac{9}{8} \sin ^{-1}\left(\frac{1}{3}\right)+\frac{\sqrt{2}}{12}\)
\( \text{Therefore, the required area is} \left[2 \times\left(\frac{9 \pi}{16}-\frac{9}{8} \sin ^{-1}\left(\frac{1}{3}\right)+\frac{\sqrt{2}}{12}\right)\right] \) \( \Rightarrow=\frac{9 \pi}{8}-\frac{9}{4} \sin ^{-1}\left(\frac{1}{3}\right)+\frac{1}{3 \sqrt{2}} \) units

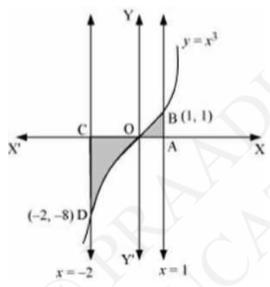
Here, the required area \( =\int_{-2}^{1} y d x \)
\(\Rightarrow=\int_{-2}^{1} x^{3} d x\)
\(\Rightarrow=\left[\frac{x^{4}}{4}\right]_{-2}^{1}\)
\(\Rightarrow=\left[\frac{1}{4}-\frac{(-2)^{4}}{4}\right]\)
\(\Rightarrow=\left(\frac{1}{4}-4\right)\)
\(\Rightarrow=-\frac{15}{4} \text { units }\)

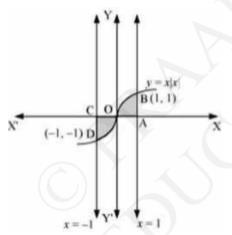
Here, the required area \( =\int_{-1}^{1} y d x \)
\(\Rightarrow=\int_{-1}^{1} x|x| d x\)
\(\Rightarrow=\int_{-1}^{0} x^{2} d x+\int_{0}^{1} x^{2} d x\)
\(\Rightarrow=\left[\frac{x^{3}}{3}\right]_{-1}^{0}+\left[\frac{x^{3}}{3}\right]_{0}^{1}\)
\(\Rightarrow=-\left(-\frac{1}{3}\right)+\frac{1}{3}\)
\( \Rightarrow=\frac{2}{3} \) units.

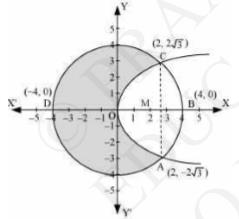
Here, the area bounded by the circle and parabola \( =2 \times[ \) Area OADO + Area ADBA]
\(\Rightarrow=2\left[\int_{0}^{2} \sqrt{16 x d x}+\int_{2}^{4} \sqrt{16-x^{2}} d x\right]\)
\(\Rightarrow=2\left[\sqrt{6}\left[\frac{x^{\frac{3}{2}}}{\frac{3}{2}}\right]_{0}^{2}\right]+2\left[\frac{x}{2} \sqrt{16-x^{2}}+\frac{16}{2} \sin ^{-1} \frac{x}{4}\right]_{2}^{4}\)
\(\Rightarrow=2 \sqrt{6} \times \frac{2}{3}\left[x^{\frac{3}{2}}\right]_{0}^{2}+2\left[8 \cdot \frac{\pi}{2}-\sqrt{16-4}-8 \sin ^{-1}\left(\frac{1}{2}\right)\right]\)
\(\Rightarrow=\frac{4 \sqrt{6}}{3}(2 \sqrt{2})+2\left[4 \pi-\sqrt{12}-8 \frac{\pi}{6}\right]\)
\(\Rightarrow=\frac{16 \sqrt{3}}{2}+8 \pi-4 \sqrt{3}-\frac{8}{3} \pi\)
\(\Rightarrow=\frac{4}{3}[\sqrt{3}+4 \pi]\)
Area of circle \( =\pi\left(\mathrm{r}^{2}\right) \)
\(=\pi(4)^{2}\)
\(=16 \pi \text { units. }\)
Thus, required area \( =16 \pi-\frac{4}{3}[4 \pi+\sqrt{3}] \)
\(\Rightarrow=\frac{4}{3}[4 \times 3 \pi-4 \pi-\sqrt{3}]\)
\(\Rightarrow=\frac{4}{3}[8 \pi-\sqrt{3}] \text { units }\)

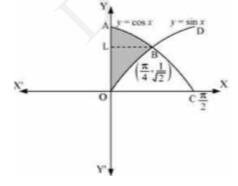
It is given that the area bounded by the y -axis, \( y=\cos x \) and \( y=\sin x \)
Thus, the required area \( = \) Area ABLA + Area OBLO
\(\Rightarrow=\int_{\frac{1}{\sqrt{2}}}^{1} x d y+\int_{0}^{\frac{1}{\sqrt{2}}} x d y\)
\(\Rightarrow=\int_{\frac{1}{\sqrt{2}}}^{1} \cos ^{-1} y d y+\int_{0}^{\frac{1}{\sqrt{2}}} \sin ^{-1} x d y\)
\(\Rightarrow=\left[y \cos ^{-1} y-\sqrt{1-y^{2}}\right]_{\frac{1}{\sqrt{2}}}^{1}+\left[x \sin ^{-1} x-\sqrt{1-x^{2}}\right]_{0}^{\frac{1}{\sqrt{2}}}\)
\(\Rightarrow=\left[\cos ^{-1}(1)-\frac{1}{\sqrt{2}} \cos ^{-1}\left(\frac{1}{\sqrt{2}}\right)+\sqrt{1-\frac{1}{2}}\right]+\left[\frac{1}{\sqrt{2}} \sin ^{-1}\left(\frac{1}{\sqrt{2}}\right)\right]+\sqrt{1-\frac{1}{2}}-1\)
\(\Rightarrow=\frac{-\pi}{4 \sqrt{2}}+\frac{1}{\sqrt{2}}+\frac{\pi}{4 \sqrt{2}}+\frac{1}{\sqrt{2}}-1\)
\(\Rightarrow=\frac{2}{\sqrt{2}}-1\)
\(\Rightarrow=\sqrt{2}-1 \text { units }\)