Class 11 maths exercise 3.1 solutions | exercise 3.1 class 11 maths solutions | class 11 ch 3 exercise 3.1 solutions | class 11 chapter 3 exercise 3.1 solution | class 11 maths ncert solutions chapter 3 | ncert solutions for class 11 maths chapter 3 | ncert exemplar class 11 maths | trigonometric functions class 11
If you’re looking for Class 11 Maths Exercise 3.1 solutions, you’ve come to the right place! Exercise 3.1 from Class 11 Chapter 3 – Trigonometric Functions is a crucial part of the NCERT syllabus. This chapter builds the foundation for understanding angles, radian and degree measure, and trigonometric identities. Our Exercise 3.1 Class 11 Maths solutions are designed to help students grasp each concept clearly with step-by-step explanations. Whether you’re solving NCERT exemplar Class 11 Maths questions or simply revising for exams, these NCERT solutions for Class 11 Maths Chapter 3 will strengthen your problem-solving skills. Covering every question from the Class 11 Ch 3 Exercise 3.1 Solutions, this guide is an essential tool for mastering Trigonometric Functions Class 11 and securing good marks.
trigonometric functions class 11 || class 11 maths ncert solutions chapter 3 || class 11 ch 3 exercise 3.1 solutions || ncert solutions for class 11 maths chapter 3 || class 11 chapter 3 exercise 3.1 solution || exercise 3.1 class 11 maths solutions || class 11 maths exercise 3.1 solutions || ncert exemplar class 11 maths
Exercise 3.1
1.
(i) Find the radian measures corresponding to the following degree measure:
\( 25^{\circ} \)
\( 25^{\circ} \)
Answer
Given: \( 25^{\circ} \)
We know that \( 180^{\circ}=\pi \) radian
\( \therefore 25^{\circ}=\frac{\pi}{180} \times 25 \) radian \( =\frac{5 \pi}{36} \) radian
(ii) Find the radian measures corresponding to the following degree measure:
\( -47^{\circ} 30^{\prime} \)
\( -47^{\circ} 30^{\prime} \)
Answer
\( -47^{\circ} 30^{\prime} \)
\( -47^{\circ} 30^{\prime}-47 \frac{1}{2} \)
\( =\frac{-95}{2} \) degree
Since \( 180^{\circ}=\pi \) radian
\( \frac{-95}{2} \) degree \( =\frac{\pi}{180} \times\left(\frac{-95}{2}\right) \) radian \( =\frac{-19}{36 \times 2} \pi \) radian \( =\frac{-19}{72} \pi \) radian
\( \therefore-47^{\circ} 30^{\prime}=\frac{-19}{72} \pi \) radian
(iii) Find the radian measures corresponding to the following degree measure:
\( 240^{\circ} \)
\( 240^{\circ} \)
Answer
\( 240^{\circ} \)
We know that \( 180^{\circ}=\pi \) radian
\( \therefore 240^{\circ}=\frac{\pi}{180} \times 240 \) radian \( =\frac{4}{3} \pi \) radian
(iv) Find the radian measures corresponding to the following degree measure:
\( 520^{\circ} \)
\( 520^{\circ} \)
Answer
\( 520^{\circ} \)
We know that \( 180^{\circ}=\pi \) radian
\( \therefore 520^{\circ}=\frac{\pi}{180} \times 520 \) radian \( =\frac{26}{9} \pi \) radian
trigonometric functions class 11 || class 11 maths ncert solutions chapter 3 || class 11 ch 3 exercise 3.1 solutions || ncert solutions for class 11 maths chapter 3 || class 11 chapter 3 exercise 3.1 solution || exercise 3.1 class 11 maths solutions || class 11 maths exercise 3.1 solutions || ncert exemplar class 11 maths
2.
(i) Find the degree measures corresponding to the following radian measure (Use \( \pi=\frac{22}{7} \) ).
\( \frac{ 11 }{ 16 } \)
\( \frac{ 11 }{ 16 } \)
Answer
\( \frac{11}{16} \)
We know that \( 180^{\circ}=\pi \) radian
\( \therefore \frac{11}{16} \) radian \( =\frac{180}{\pi} \times \frac{11}{16} \) degree \( =\frac{45 \times 11}{\pi \times 4} \) degree
\( =\frac{45 \times 11 \times 7}{22 \times 4} \) degree \( =\frac{315}{8} \) degree
\( =36 \frac{3}{8} \) degree
\( =39^{\circ}+\frac{3 \times 60}{8} \) minutes \( \left[1^{\circ}=60^{\prime}\right] \)
\( =39^{\circ}+22^{\prime}+\frac{1}{2} \) minutes
\( =39^{\circ} 22^{\prime} 30^{\prime \prime} \)
(ii) Find the degree measures corresponding to the following radian measure (Use \( \pi=\frac{22}{7} \) ).
\(-4\)
\(-4\)
Answer
\(-4\)
We know that \( \pi \) radian \( =180^{\circ} \)
\(-4 \text { radian }=\frac{180}{\pi} \times(-4) \text { degree }=\frac{180 \times 7(-4)}{22} \text { degree }\)
\(=\frac{-2520}{11} \text { degree }=-229 \frac{1}{11} \text { degree }\)
\(=-229^{\circ}+\frac{1 \times 60}{11} \text { degree }\left[1^{\circ}=60^{\prime}\right]\)
\(=-229^{\circ}+5^{\prime}+\frac{5}{11} \text { minutes }\)
\(=-229^{\circ} 5^{\prime} 27^{\prime}\)
(iii) Find the degree measures corresponding to the following radian measure (Use \( \pi=\frac{22}{7} \) ).
\( \frac{ 5 \pi }{ 3 } \)
\( \frac{ 5 \pi }{ 3 } \)
Answer
\( \frac{5 \pi}{3} \)
We know that \( \pi \) radian \( =180^{\circ} \)
\(\therefore \frac{5 \pi}{3} \text { radian }=\frac{180}{\pi} \times \frac{5 \pi}{3} \text { degree }=300^{\circ}\)
(iv) Find the degree measures corresponding to the following radian measure (Use \( \pi=\frac{22}{7} \) ).
\( \frac{ 7 \pi }{ 6 } \)
\( \frac{ 7 \pi }{ 6 } \)
Answer
\( \frac{7 \pi}{6} \)
We know that \( \pi \) radian \( =180^{\circ} \)
\(\therefore \frac{7 \pi}{6} \text { radian }=\frac{180}{\pi} \times \frac{7 \pi}{6}=210^{\circ}\)
trigonometric functions class 11 || class 11 maths ncert solutions chapter 3 || class 11 ch 3 exercise 3.1 solutions || ncert solutions for class 11 maths chapter 3 || class 11 chapter 3 exercise 3.1 solution || exercise 3.1 class 11 maths solutions || class 11 maths exercise 3.1 solutions || ncert exemplar class 11 maths
3. A wheel makes 360 revolutions in one minute. Through how many radians does it turn in one second?
Answer
Number of revolutions made by the wheel in 1 minutes \( =360 \)
\( \therefore \) Number of revolutions made by the wheel in 1 second \( =\frac{360}{60}=6 \)
In one complete revolution, the wheel turns an angle of \( 2 \pi \) radian.
Hence, in 6 complete revolutions, it will turn an angle of \( 6 \times 2 \pi \) radian. i.e., \( 12 \pi \) radian.
4. Find the degree measure of the angle subtended at the center of a circle of radius 100 cm by an arc of length 22 cm (Use \( \pi=\frac{22}{7} \) ).
Answer
We know that in a circle of radius \( r \) unit, if an arc of length 1 unit subtends an angle \( \theta \) radian at the center, then
\(\theta=\frac{1}{r}\)
Therefore, for \( 1=22 \mathrm{~cm} \) (length of arc) and \( \mathrm{r}=100 \mathrm{~cm} \) (radius of circle)
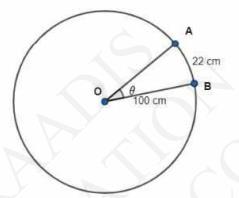
\( \theta=\frac{22}{100} \) radian \( =\frac{180}{\pi} \times \frac{22}{100} \) degree \( =\frac{180 \times 7 \times 22}{22 \times 100} \) degree
\( =\frac{126}{10} \) degree \( =12 \frac{3}{5} \) degree \( =12^{\circ} 36^{\prime}\left[1^{\circ}=60^{\prime}\right] \)
Thus, the required angle is \( 12^{\circ} 36^{\prime} \)
5. In a circle of diameter 40 cm , the length of a chord is 20 cm . Find the length of minor arc of the chord.
Answer
Given: A circle of diameter 40 cm
\(\Rightarrow \text { radius }=\frac{40}{2}=20 \mathrm{~cm}\)
The length of a chord is 20 cm .
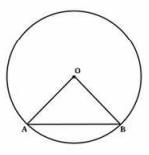
In \( \triangle \mathrm{OAB}, \mathrm{OA}=\mathrm{OB}= \) Radius of circle \( =20 \mathrm{~cm} \)
Also, \( \mathrm{AB}=20 \mathrm{~cm} \)
Thus, \( \triangle \mathrm{OAB} \) is an equilateral triangle.
\( \therefore \theta=60^{\circ}=\frac{\pi}{3} \) radian
We know that in a circle of radius \( r \) unit, if an arc of length 1 unit subtends an angle \( \theta \) radian at the center them.
\( \theta=\frac{1}{r} \)
\( \frac{\pi}{3}=\frac{A B}{20}=A B=\frac{20 \pi}{3} \mathrm{~cm} \)
Thus, the length of the minor arc of the chord is \( \frac{20 \pi}{3} \mathrm{~cm} \)
6. If in two circles, arcs of the same length subtend angles \( 60^{\circ} \) and \( 75^{\circ} \) at the center, find the ratio of their radii.
Answer
Let, the radii of the two circles be \( r_{1} \) and \( r_{2} \). Let, an arc of length 1 subtends an angle of \( 60^{\circ} \) at the center of the circle of radius \( r_{2} \), while let an arc of length/subtend an angle of \( 75^{\circ} \) at the center of circle of radius \( \mathrm{r}_{2} \).
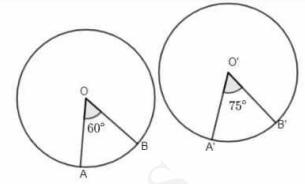
Now, \( 60^{\circ}=\frac{\pi}{3} \) radian and \( 75^{\circ}=\frac{5 \pi}{12} \) radian
We know that in a circle of radius \( r \) unit, if an arc of length 1 unit subtends an angle \( \theta \) radian at the center then.
7.
(i) Find the angle in radian through which a pendulum swings if its length is 75 cm and the tip describes an arc of length 10 cm
Answer
We know that in a circle of radius r unit, if an arc of length 1 unit subtends
An angle \( \theta \) radian at the center, \( \theta \) then \( =\frac{1}{r} \)
It is given that \( \mathrm{r}=75 \mathrm{~cm} \)
Here, \( 1=10 \mathrm{~cm} \)
\( \theta=\frac{10}{75} \) radian \( =\frac{2}{15} \) radian
(ii) Find the angle in radian through which a pendulum swings if its length is 75 cm and the tip describes an arc of length 15 cm
Answer
We know that in a circle of radius r unit, if an arc of length 1 unit subtends
An angle \( \theta \) radian at the center, \( \theta \) then \( =\frac{1}{r} \)
It is given that \( \mathrm{r}=75 \mathrm{~cm} \)
Here, \( 1=15 \mathrm{~cm} \)
\( \theta=\frac{15}{75} \) radian \( =\frac{1}{5} \) radian
(iii) Find the angle in radian through which a pendulum swings if its length is 75 cm and the tip describes an arc of length 21 cm
Answer
We know that in a circle of radius r unit, if an arc of length 1 unit subtends
An angle \( \theta \) radian at the center, \( \theta \) then \( =\frac{1}{r} \)
It is given that \( \mathrm{r}=75 \mathrm{~cm} \)
Here, \( 1=21 \mathrm{~cm} \)
\( \theta=\frac{21}{25} \) radian \( \frac{7}{25} \) radian
