Class 11 maths exercise 3.2 solutions | exercise 3.2 class 11 maths solutions | class 11 ch 3 exercise 3.2 solutions | class 11 chapter 3 exercise 3.2 solution | class 11 maths ncert solutions chapter 3 | ncert solutions for class 11 maths chapter 3 | ncert exemplar class 11 maths | trigonometric functions class 11
If you’re searching for Class 11 Maths Exercise 3.2 solutions, you’ve come to the right place. Our detailed and accurate Exercise 3.2 Class 11 Maths solutions help students grasp the core concepts of Trigonometric Functions Class 11 with ease. Covering every question from Class 11 Chapter 3 Exercise 3.2 solutions, this resource aligns perfectly with the NCERT Solutions for Class 11 Maths Chapter 3. Whether you’re practicing from the textbook or referring to the NCERT Exemplar Class 11 Maths, these step-by-step solutions will strengthen your understanding and boost your confidence.

class 11 maths ncert solutions chapter 3 || class 11 chapter 3 exercise 3.2 solution || trigonometric functions class 11 || exercise 3.2 class 11 maths solutions || ncert solutions for class 11 maths chapter 3 || ncert exemplar class 11 maths || class 11 ch 3 exercise 3.2 solutions || class 11 maths exercise 3.2 solutions
Exercise 3.2
\( 1 \cos x=-\frac{1}{2}, x \) lies in third quadrant.
Answer
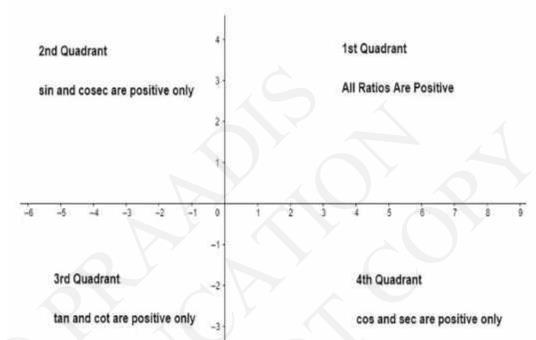
\(\operatorname{Cos} x=-\frac{1}{2}\)
\(\therefore \sec x=\frac{1}{\cos x}=\frac{1}{\left(-\frac{1}{2}\right)}=-2\)
\(=\sin ^{2} x+\cos ^{2} x=1\)
\(=\sin ^{2} x=1-\cos ^{2} x\)
\(=\sin ^{2} x=1-\left(-\frac{1}{2}\right)^{2}\)
\(=\sin ^{2} x=1-\frac{1}{4}=\frac{3}{4}\)
\(=\sin x= \pm \frac{\sqrt{3}}{2}\)
Since \( x \) lies in the \( 3^{\text {rd }} \) quadrant, the value of \( \sin x \) will be negative.
\( \therefore \sin x=-\frac{\sqrt{3}}{2} \)
\( \operatorname{Cosec} x=\frac{1}{\sin x}=\frac{1}{\left(-\frac{\sqrt{3}}{2}\right)}=-\frac{2}{\sqrt{3}} \)
\( \tan x=\frac{\sin x}{\cos x}=\frac{\left(-\frac{\sqrt{3}}{2}\right)}{\left(-\frac{1}{2}\right)}=\sqrt{3} \)
\( \cot x=\frac{1}{\tan x}=\frac{1}{\sqrt{3}} \)
class 11 maths ncert solutions chapter 3 || class 11 chapter 3 exercise 3.2 solution || trigonometric functions class 11 || exercise 3.2 class 11 maths solutions || ncert solutions for class 11 maths chapter 3 || ncert exemplar class 11 maths || class 11 ch 3 exercise 3.2 solutions || class 11 maths exercise 3.2 solutions
2. \( \sin x=\frac{3}{5}, x \) lies in second quadrant.
Answer
\( \operatorname{Sin} x=\frac{3}{5} \)
\( \operatorname{Cosec} x=\frac{1}{\sin x}=\frac{1}{\frac{3}{5}}=\frac{5}{3} \)
\( \operatorname{Sin}^{2} x+\cos ^{2} x=1 \)
\( \operatorname{Cos}^{2} x=1-\sin ^{2} x \)
\( \operatorname{Cos}^{2} x=1-\left(\frac{3}{5}\right)^{2} \)
\( \operatorname{Cos}^{2} x=1-\frac{9}{25}=\frac{25-9}{25} \)
\( \operatorname{Cos}^{2} x=\frac{16}{25} \)
\( =\cos x= \pm \frac{4}{5} \)
Since \( x \) lies in the \( 2^{\text {nd }} \) quadrant, the value of \( \cos x \) will be negative
\(\therefore \cos x=-\frac{4}{5}\)
\(\sec x=\frac{1}{\cos x}=\frac{1}{\left(-\frac{4}{5}\right)}=-\frac{5}{4}\)
\(\tan x=\frac{\sin x}{\cos x}=\frac{\left(\frac{3}{5}\right)}{\left(-\frac{4}{5}\right)}=-\frac{3}{4}\)
\(\cot x=\frac{1}{\tan x}=-\frac{4}{3}\)
3. \( \cot x=\frac{3}{4}, x \) lies in third quadrant.


Answer
\( \operatorname{Cot} x=\frac{3}{4} \)
\(\tan x=\frac{1}{\cot x}=\frac{1}{\left(\frac{3}{4}\right)}=\frac{4}{3}\)
\(1+\tan ^{2} x=\sec ^{2} x\)
\(1+\left(\frac{3}{4}\right)^{2}=\sec ^{2} x\)
\(1+\frac{9}{16}=\sec ^{2} x\)
\(\frac{16+9}{16}=\sec ^{2} x\)
\(\operatorname{Sec}^{2} x=\frac{25}{16}\)
\(\operatorname{Sec}= \pm \frac{5}{3}\)
Since \( x \) lies in the \( 3^{\text {rd }} \) quadrant, the value of \( \sec x \) will be negative
\( \therefore \sec x=-\frac{5}{3} \)
\( \operatorname{Cos} x=\frac{1}{\sec x}=\frac{1}{\left(-\frac{5}{3}\right)}=-\frac{3}{5} \)
\( \tan x=\frac{\sin x}{\cos x}=\frac{4}{3}=\frac{\sin x}{\left(\frac{-3}{5}\right)}\)
\( =\sin x=\frac{4}{3} \times \frac{-3}{5}=-\frac{4}{5} \)
\( \operatorname{Cosec} x=\frac{1}{\sin x}=-\frac{5}{4} \)
4. \( \sec x=\frac{13}{5}, x \) lies in fourth quadrant.
Answer
\(\operatorname{Sec} x=\frac{13}{5}\)
\(\operatorname{Cos} x=\frac{1}{\sec x}=\frac{1}{\left(\frac{13}{5}\right)}=\frac{5}{13}\)
\(\operatorname{Sin}^{2} x+\cos ^{2} x=1\)
\(\operatorname{Sin}^{2} x=1-\cos ^{2} x\)
\( \operatorname{Sin}^{2} x=1-\left(\frac{5}{13}\right)^{2} \)
\( \operatorname{Sin}^{2} x=1-\frac{25}{169} \)
\( \operatorname{Sin}^{2} x=\frac{169-25}{169} \)
\( \operatorname{Sin}^{2} x=\frac{144}{169} \)
\( \operatorname{Sin} x= \pm \frac{12}{13} \)
Since \( x \) lies in the \( 4^{\text {th }} \) quadrant, the value of \( \sin x \) will be negative
\( \therefore \sin x=-\frac{12}{13} \)
\( \operatorname{Cosec} x=\frac{1}{\sin x}=\frac{1}{\left(-\frac{12}{13}\right)}=-\frac{13}{12} \)
\( \tan x=\frac{\sin x}{\cos x}=\frac{\left(-\frac{12}{13}\right)}{\left(\frac{5}{13}\right)}=-\frac{12}{5} \)
\( \cot x=\frac{1}{\tan x}=\frac{1}{\left(-\frac{12}{13}\right)}=-\frac{5}{12} \)
5. \( \tan x=-\frac{5}{12}, x \) lies in second quadrant.
Answer
\(\tan x=-\frac{5}{12}\)
\(\cot x=\frac{1}{\tan x}=\frac{1}{\left(-\frac{5}{12}\right)}=-\frac{12}{5}\)
\(1+\tan ^{2} x=\sec ^{2} x\)
\(1+\left(-\frac{5}{12}\right)^{2}=\sec ^{2} x\)
\(1+\frac{25}{144}=\sec ^{2} x\)
\(\frac{144+25}{144}=\sec ^{2} x\)
\(\frac{169}{144}=\sec ^{2} x\)
\( \operatorname{Sec} x= \pm \frac{13}{12} \)
Since \( x \) lies in the \( 2^{\text {nd }} \) quadrant, the value of \( \sec x \) will be negative
\( \therefore \sec x=-\frac{13}{12} \)
\( \operatorname{Cos} x=\frac{1}{\sec x}=\frac{1}{\left(-\frac{13}{12}\right)}=-\frac{12}{13} \)
\( \tan x=\frac{\sin x}{\cos x}=-\frac{5}{12}=\frac{\sin x}{\left(-\frac{12}{13}\right)} \)
\( \sin x=\frac{5}{12} \times\left(-\frac{12}{13}\right)=\frac{5}{13} \)
\( \operatorname{cosec} x=\frac{1}{\sin x}=\frac{1}{\left(\frac{5}{13}\right)}=\frac{13}{5} \)
class 11 maths ncert solutions chapter 3 || class 11 chapter 3 exercise 3.2 solution || trigonometric functions class 11 || exercise 3.2 class 11 maths solutions || ncert solutions for class 11 maths chapter 3 || ncert exemplar class 11 maths || class 11 ch 3 exercise 3.2 solutions || class 11 maths exercise 3.2 solutions
6. Find the values of the trigonometric functions.
\(\sin 765^{\circ}\)
\(\sin 765^{\circ}\)
Answer
It is known that the value of \( \sin x \) repeats after an interval of \(2 n\) or \( 360^{\circ} \)
\(\therefore \sin 765^{\circ}=\sin \left(2 \times 360^{\circ}+45^{\circ}\right)=\sin 45^{\circ}=\frac{1}{\sqrt{2}}\)
7. Find the values of the trigonometric functions. \( \operatorname{cosec}\left(-1410^{\circ}\right) \)
Answer
It is known the value of \( \operatorname{cosec} x \) repeat after an interval of \(2 n\) or \( 360^{\circ} \)
\(\therefore \operatorname{cosec}\left(-1410^{\circ}\right)=\operatorname{cosec}\left(-1410^{\circ}+4 \times 360^{\circ}\right)\)
\(=\operatorname{cosec}\left(-1410^{\circ}+1440^{\circ}\right)\)
\(=\operatorname{cosec} 30^{\circ}=2\)
8. Find the values of the trigonometric functions.
\(\tan \frac{19 \pi}{3}\)
\(\tan \frac{19 \pi}{3}\)
Answer
It is known the value of \( \tan x \) repeat after an interval of \(2 n\) or \( 360^{\circ} \)
\(\therefore \tan \frac{19 \pi}{3}=\tan 6 \frac{1}{3} \pi=\tan \left(6 \pi+\frac{\pi}{3}\right)=\tan \frac{\pi}{3}=\tan 60^{\circ}=\sqrt{3}\)
9. Find the values of the trigonometric functions.
\(\sin \left(-\frac{11 \pi}{3}\right)\)
\(\sin \left(-\frac{11 \pi}{3}\right)\)
Answer
It is known the value of \( \sin x \) repeat after an interval of \(2 n\) or \( 360^{\circ} \)
\(\therefore \sin \left(-\frac{11 \pi}{3}\right)=\sin \left(-\frac{11 \pi}{3}+2 \times 2 \pi\right)=\sin \frac{\pi}{3}=\frac{\sqrt{3}}{2}\)
10. Find the values of the trigonometric functions.
\(\operatorname{Cot}\left(-\frac{15 \pi}{4}\right)\)
\(\operatorname{Cot}\left(-\frac{15 \pi}{4}\right)\)
Answer
It is known the value of \( \cot x \) repeat after an interval of \(2 n\) or \( 360^{\circ} \)
\(\therefore \cot \left(-\frac{15 \pi}{4}\right)=\cot \left(-\frac{15 \pi}{4}+4 \pi\right)=\cot \frac{\pi}{4}=1\)

