Class 9 Maths Chapter 8 Exercise 8.2

(i) In \( \triangle A D C, S \) and \( R \) are the mid-points of sides \( A D \) and \( C D \) respectively
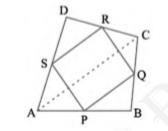
Midpoint theorem: In a triangle, the line segment joining the mid-points of any two sides of the triangle is parallel to the third side and is half of it \( \mathrm{SR} \| \mathrm{AC} \) and \( \mathrm{SR}=\frac{1}{2} \mathrm{AC} \ldots(1)\) [By mid-point theorem]
(ii) In \( \triangle \mathrm{ABC}, \mathrm{P} \) and Q are mid-points of sides AB and BC respectively. Therefore, by using mid-point theorem
\(\mathrm{PQ} \| \mathrm{AC} \text { and } \mathrm{PQ}=\frac{1}{2} \mathrm{AC}\ldots(2)\)
Using equations (1) and (2), we obtain
\(\mathrm{PQ} \| \mathrm{SR} \text { and } \mathrm{PQ}=\mathrm{SR}\ldots(3)\)
\(\mathrm{PQ}=\mathrm{SR}\)
(iii) From equation (3), we obtained
\( P Q \| S R \) and
\(\mathrm{PQ}=\mathrm{SR}\)
Clearly, one pair of opposite sides of quadrilateral PQRS is parallel and equal
Hence, PQRS is a parallelogram

The figure is given below:

To Prove: PQRS is a rectangle.
For that, we need to prove that, \( \mathrm{PQ}=\mathrm{RS}, \mathrm{PS}=\mathrm{QR} \) and also, that angles of PQRS are all right angles.
Proof:
We start by proving the equality of sides of quadrilateral \( \operatorname{PQRS} \)
In \( \triangle A B C, P \) and \( Q \) are the mid-points of sides \( A B \) and \( B C \) respectively,
The Midpoint Theorem states that the segment joining two sides of a triangle at the midpoints
of those sides is parallel to the third side and is half the length of the third side.
\( \therefore \) From the mid-point theorem, \( \mathrm{PQ} \| A C \& \)
\(\mathrm{PQ}=\frac{1}{2} \mathrm{AC}\ldots(1)\)
Also, R and S are the mid-points of CD and AD respectively
\( \therefore \) From the mid-point theorem,
\(RS || AC\)
\( \& R S=\frac{1}{2} \mathrm{AC} \ldots(2)\)
Therefore,
From equations (1) and (2), we obtain \( P Q \| R S \) and \( P Q=R S \)
Since in quadrilateral \(PQRS \), one pair of opposite sides is equal and parallel to each other
So it is a parallelogram.
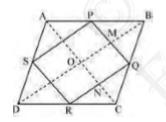
Let the diagonals of rhombus ABCD intersect each other at point O
In quadrilateral \(OMQN\),
\(MQ \| ON (\text{Because} PQ \| AC)\)
\(QN|| OM (\text{Because} QR || BD)\)
Therefore,
\(OMQN\) is a parallelogram
\(\angle \mathrm{MQN}=\angle \mathrm{NOM}\)
\(\angle \mathrm{PQR}=\angle \mathrm{NOM}\)
However, \( NOM =900 \) (Diagonals of a rhombus are perpendicular to each other)
So, \( \mathrm{PQR}=900 \)
Clearly, \(PQRS\) is a parallelogram having one of its interior angles as \(900\)
Hence, \(PQRS\) is a rectangle
Hence, Proved.

Let us join AC and BD .
In \( \triangle \mathrm{ABC} \),
P and Q are the mid-points of AB and BC respectively

To Prove: PQRS is a rhombus.
Proof:
The Midpoint Theorem states that the segment joining two sides of a triangle at the midpoints of those sides is parallel to the third side and is half the length of the third side.
\( \mathrm{PQ} \| \mathrm{AC} \) and \( \mathrm{PQ}=\mathrm{AC} \) (Mid-point theorem) \(\ldots(1)\)
Similarly, in \( \triangle \mathrm{ADC} \),
\( \mathrm{SR} \| \mathrm{AC} \) and \( \mathrm{SR}=\frac{1}{2} \mathrm{AC} \) (Mid-point theorem) \(\ldots(2)\)
Clearly,
\( P Q \| S R \) and \( P Q=\frac{1}{2} S R \)
Since in quadrilateral PQRS, one pair of opposite sides is equal and parallel to each other, it is a parallelogram
\(PS \| QR\) and \(PS = QR\) (Opposite sides of parallelogram) \(\ldots(3)\)
In \( \triangle B C D, Q \) and \( R \) are the mid-points of side \( B C \) and \( C D \) respectively. \( \mathrm{QR} \| \mathrm{BD} \) and \( \mathrm{QR}=\frac{1}{2} \mathrm{BD} \) (Mid-point theorem) \(\ldots(4)\)
However, the diagonals of a rectangle are equal.
\( \mathrm{AC}=\mathrm{BD} \ldots(5) \)
By using equation (1), (2), (3), (4), and (5), we obtain
\(\mathrm{PQ}=\mathrm{QR}=\mathrm{SR}=\mathrm{PS}\)
Now, as all sides of the rhombus are equal.
Hence, PQRS is a rhombus.

Let EF intersect DB at G
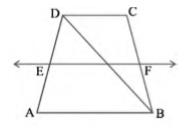
By converse of mid-point theorem, we know that a line drawn through the mid-point of any side of a triangle and parallel to another side, bisects the third side

In \( \triangle \mathrm{ABD} \),
\( \mathrm{EF} \| \mathrm{AB} \) and E is the mid-point of AD
Therefore,
G will be the mid-point of DB
\( \mathrm{EF} \| \mathrm{AB} \) and
\( \mathrm{AB} \| \mathrm{CD} \)
\( \mathrm{EF} \| \mathrm{CD} \) (Two lines parallel to the same line are parallel to each other)
In \( \triangle B C D \),
\( \mathrm{GF} \| \mathrm{CD} \) and
G is the mid-point of line BD. Therefore, by using converse of mid-point theorem, F is the mid-point of BC

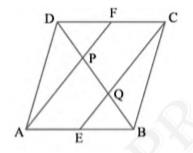
ABCD is a parallelogram.
So, \( \mathrm{AB} \| \mathrm{CD} \)
\( \Rightarrow \mathrm{AE} \| \mathrm{FC} \)
Also \( \mathrm{AB}=\mathrm{CD} \)
(Opposite sides of parallelogram ABCD )
\( \Rightarrow \mathrm{AE}=\mathrm{FC} \)
(Since E and F are midpoints of AB and CD )
In quadrilateral AECF, one pair of opposite sides are equal and parallel.
\( \therefore \) AECF is a parallelogram.
Then,
\(AE \| FC\)
Again,
\(\mathrm{AB}=\mathrm{CD}(\text { Opposite sides of parallelogram } A B C D)\)
\(\mathrm{AB}=\mathrm{CD}\)
\(\mathrm{AE}=\mathrm{FC}(\mathrm{E} \text { and } \mathrm{F} \text { are mid-points of side } \mathrm{AB} \text { and } C D)\)
In quadrilateral AECF, one pair of opposite sides is parallel and equal to each other
Therefore, AECF is a parallelogram
\(AF|| EC\) (Opposite sides of a parallelogram)
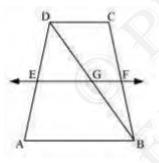
In \( \triangle \mathrm{DQC} \),
F is the mid-point of side DC and FP \( \| \) CQ
Therefore, by using the converse of mid-point theorem, it can be said that \( P \) is the mid-point of DQ
\(\mathrm{DP}=\mathrm{PQ}\ldots(1)\)
\(\frac{1}{2} \mathrm{AB}=\frac{1}{2} \mathrm{CD}\)
Similarly,
In \( \triangle \mathrm{APB} \),
\( E \) is the mid-point of side \( A B \) and \( E Q \| A P \)
Therefore, by using the converse of mid-point theorem, it can be said that \(Q\) is the mid-point of \(PB\)
\(\mathrm{PQ}=\mathrm{QB}\ldots(2)\)
From equations (1) and (2),
\(D P=P Q=B Q\)
Hence, the line segments \(AF\) and \(EC\) trisect the diagonal \(BD \).

Midpoint theorem: The line segment joining the mid-points of two sides of a triangle is parallel to the third side and equal to half the third side.
Let \( A B C D \) is a quadrilateral in which \( P, Q, R \), and \( S \) are the mid-points of sides \( A B, B C, C D \), and \( D A \) respectively. Join \( P Q, Q R, R S, S P \), and \( B D \).

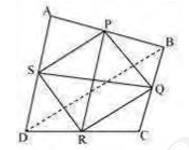
In \( \triangle \mathrm{ABD}, \mathrm{S} \) and P are the mid-points of AD and AB respectively. Therefore, by using mid-point theorem:
\( \mathrm{SP} \| \mathrm{BD} \) and \( \mathrm{SP}=\frac{1}{2} \mathrm{BD} \ldots(1)\)
Similarly, in \( \triangle \mathrm{BCD} \),
\( \mathrm{QR} \| \mathrm{BD} \) and \( \mathrm{QR}=\frac{1}{2} \mathrm{BD} \ldots(2)\)
From equations (1) and (2), we obtain
\( \mathrm{SP} \| \mathrm{QR} \) and \( \mathrm{SP}=\mathrm{QR} \)
In quadrilateral \(SPQR\), one pair of opposite sides is equal and parallel to each other
Therefore, \(SPQR\) is a parallelogram.
We know that diagonals of a parallelogram bisect each other
Hence, \(PR\) and \(QS\) bisect each other.

(i) In \( \triangle A B C \),

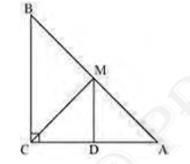
Given that: M is the mid-point of \( A B \) and \( \mathrm{MD} \| \mathrm{BC} \)
Therefore,
The Midpoint Theorem states that the segment joining two sides of a triangle at the midpoints of those sides is parallel to the third side and is half the length of the third side.
D is the mid-point of AC (By converse of mid-point theorem)
(ii) As \( \mathrm{DM} \| \mathrm{CB} \) and AC is a transversal line for them
Therefore, \( \angle \mathrm{MDC}+\angle \mathrm{DCB}=180^{\circ} \) (Co-interior angles)
\(\angle \mathrm{MDC}+90^{\circ}=180^{\circ}\)
\(\angle \mathrm{MDC}=90^{\circ}\)
MD is perpendicular to AC
(iii) Join MC
In \( \triangle \mathrm{AMD} \) and \( \Delta \mathrm{CMD} \),
\( \mathrm{AD}=\mathrm{CD} \) ( D is the mid-point of side AC\( ) \)
\( \angle \mathrm{ADM}=\angle \mathrm{CDM}\left(\right. \) Each \( \left.90^{\circ}\right) \)
\( \mathrm{DM}=\mathrm{DM} \) (Common)
Two sides and included angle (SAS) Definition: Triangles are congruent if any pair of corresponding sides and their included angles are equal in both triangles.
\( \Delta \mathrm{AMD} \cong \Delta \mathrm{CMD}( \) By SAS congruence rule \( ) \)
Therefore,
\( \mathrm{AM}=\mathrm{CM}(\mathrm{By} \) CPCT \( ) \)
However,
\( A M=\frac{1}{2} A B \) ( \( M \) is the mid-point of \( A B \) )
Therefore,
\(\mathrm{CM}=\mathrm{AM}=\frac{1}{2} \mathrm{AB}\)