Number system class 9 extra questions || class 9 maths ncert solution up board || exercise 1.5 class 9 maths || ncert exemplar class 9 maths solutions || number system questions with solutions || ncert exemplar class 9 maths solutions chapter 1 || ncert solutions for class 9 maths || class 9 maths chapter 1 exercise 1.5 solutions || cbse class 9 maths chapter 1 exercise 1.5 solutions
Searching for NCERT Class 9 Maths Chapter 1 Exercise 1.5 solutions? You’re in the right place! This section provides simple, step-by-step solutions for all the problems in Exercise 1.5 of Chapter 1 – Number Systems. This part of the chapter focuses on the laws of rational exponents with real numbers, helping students understand how to work with numbers in exponential form. It builds a strong foundation for dealing with powers and roots in higher classes. These solutions are crafted to enhance both conceptual clarity and problem-solving speed. Whether you’re revising for exams or just trying to strengthen your basics, this guide will make your study of exponents and real numbers both effective and student-friendly.

number system class 9 extra questions || class 9 maths ncert solution up board || exercise 1.5 class 9 maths || ncert exemplar class 9 maths solutions || number system questions with solutions || ncert exemplar class 9 maths solutions chapter 1 || ncert solutions for class 9 maths || class 9 maths chapter 1 exercise 1.5 solutions || cbse class 9 maths chapter 1 exercise 1.5 solutions
Exercise 1.5
1.
(i) Classify the following numbers as rational or irrational: \(
2-\sqrt{5} \)
Answer
\( 2-\sqrt{5} \)\(=2-2.2360679 \ldots\)
\(=-0.2360679 \ldots\)
Since the number is in non-terminating non-recurring, therefore, it is an irrational number
(ii) Classify the following numbers as rational or irrational: \(
(3+\sqrt{23})-\sqrt{23} \)
Answer
\( (3+\sqrt{23})-\sqrt{23}=3+\sqrt{23}-\sqrt{23} \)\( =3 \)
\( =\frac{3 }{ 1} \)
A number is a rational number as it can be represented in the form of \(\frac{\mathrm{p}}{\mathrm{q}}\).
(iii) Classify the following numbers as rational or irrational:
\( \frac{2 \sqrt{7}}{7 \sqrt{7}} \)
Answer
\( \frac{2 \sqrt{7}}{7 \sqrt{7}}=\frac{2 }{ 7 }\)The number is a rational number as it can be represented in the form of \(\frac{\mathrm{p}}{\mathrm{q}}\).
(iv) Classify the following numbers as rational or irrational: \(
\frac{1}{\sqrt{2}} \)
Answer
\( \frac{1}{\sqrt{2}}=\frac{\sqrt{2}}{2} \) \(=0.7071067811 \ldots . .\)
Since the number is a non-terminating and non-recurring number.
Hence, it is an irrational number
(v) Classify the following numbers as rational or irrational: \(
2 \pi \)
Answer
\( 2 \pi=2 \times 3.1415 \ldots \)\(=6.2830 \ldots \ldots\)
Since the number is a non-terminating and non-recurring number.
Hence, it is an irrational number
2.
number system class 9 extra questions || class 9 maths ncert solution up board || exercise 1.5 class 9 maths || ncert exemplar class 9 maths solutions || number system questions with solutions || ncert exemplar class 9 maths solutions chapter 1 || ncert solutions for class 9 maths || class 9 maths chapter 1 exercise 1.5 solutions || cbse class 9 maths chapter 1 exercise 1.5 solutions
(i) Simplify each of the following expressions: \(
(3+\sqrt{3})(2+\sqrt{2}) \)
Answer
\((3+\sqrt{3} )(2+\sqrt{2} )\)\(= 3(2+\sqrt{2} )+\sqrt{3}(2+\sqrt{2})\)
\(= 3 \times 2+3 \sqrt{2} +2 \sqrt{3} +\sqrt{2} \times \sqrt{3} \)
\(= 6+3 \sqrt{2} +2 \sqrt{3} +\sqrt{6}\)
(ii) Simplify each of the following expressions: \(
(3+\sqrt{3})(3-\sqrt{3}) \)
Answer
\((3+\sqrt{3})(3-\sqrt{3}) \quad\) [Since, \(
(a+b)(a-b)=a^{2}-b^{2}] \)\(=3^{2}-(\sqrt{3})^{2}\)
\(=9-3\)
\(=6\)
(iii) Simplify each of the following expressions: \(
(\sqrt{5}+\sqrt{2})^{2} \)
Answer
\( (\sqrt{5}+\sqrt{2 } )^{2} \quad\)
[Since,\((a+b)^{2}=a^{2}+b^{2}+2 a b\)]\(=(\sqrt{5})^{2}+(\sqrt{2} )^{2}+2 \times \sqrt{5} \times \sqrt{2}\)
\(=5+2+2 \times\sqrt{10}\)
\(=7+2 \sqrt{ 10} \)
(iv) Simplify each of the following expressions: \(
(\sqrt{5}-\sqrt{2})(\sqrt{5}+\sqrt{2}) \)
Answer
\((\sqrt{ } 5-\sqrt{ } 2)(\sqrt{5}+\sqrt{ } 2)\quad\) [Since,
\((a+b)(a-b)=a^{2}-b^{2}\)]\(=(\sqrt{ } 5)^{2}-(\sqrt{ } 2)^{2}\)
\(=5-2\)
\(=3\)
3. Recall, \( \pi \) is defined as the ratio of the circumference
(say c) of a circle to its diameter (say d). That is \(
\pi=\frac{c}{d} \), This seems to contradict the fact that \( \pi
\) is irrational. How will you resolve this contradiction?
Answer
There is no contradiction in the statement.When we measure any value with a scale, we only obtain an approximate value.
We never obtain an accurate value.
Hence, we cannot say that either c or d is irrational.
The value of \( \pi \) is almost equal to \( \frac{22 }{ 7 }\) or \( 3.142857 \ldots \)
number system class 9 extra questions || class 9 maths ncert solution up board || exercise 1.5 class 9 maths || ncert exemplar class 9 maths solutions || number system questions with solutions || ncert exemplar class 9 maths solutions chapter 1 || ncert solutions for class 9 maths || class 9 maths chapter 1 exercise 1.5 solutions || cbse class 9 maths chapter 1 exercise 1.5 solutions
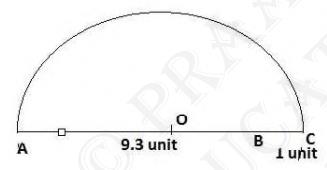
4. Represent \( \sqrt{9.3} \) on the number line.
Answer
Step 1: Draw a line segment \( A B \) of \(9.3\) unit. Then,
extend it to \(C\) so that \( \mathrm{BC}=1 \) unit.
Step 2: Now, \( A C=10.3 \) units. Find the center of \( A C \) and mark it as \( O \)

Step 3: Draw a semi-circle with radius \(OC\) and center \(O\).
Step 4: Draw a perpendicular line \(BD\) to \(AC\) at point \(B\) intersecting the semi-circle at \(D\). And then, join \(OD\)
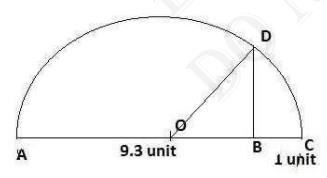
Step 5: Now, \(OBD\) is a right angled triangle
Here, \(OD\) (Radius of semi-circle)
\(\mathrm{OC}=\frac{10.3}{2}\)
\(\mathrm{BC}=1\)
Then, \( \mathrm{OB}=\mathrm{OC}-\mathrm{BC} \)
Using Pythagoras theorem,
\(\mathrm{OD}^{2}=\mathrm{BD}^{2}+\mathrm{OB}^{2}\)
\(\left(\frac{10.3}{2}\right)^{2}=\mathrm{BD}^{2}+\left(\frac{8.3}{2}\right)^{2}\)
\(\mathrm{BD}^{2}=\left(\frac{10.3}{2}\right)^{2}-\left(\frac{8.3}{2}\right)^{2}\)
\(\mathrm{BD}^{2}=\left(\frac{10.3}{2}-\frac{8.3}{2}\right)\left(\frac{10.3}{2}+\frac{8.3}{2}\right)\)
\(\mathrm{BD}^{2}=9.3\)
\(\mathrm{BD}=\sqrt{9.3}\)
Thus, the length of BD is \( \sqrt{9.3} \)
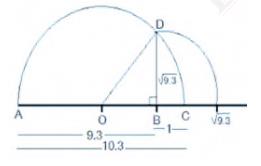
Step 6: Taking \(BD\) as radius and \(B\) as the center, construct an arc which touches the line segment.
Now, the point where it touches the line segment is at a distance of from \(O\) as shown in the figure below
5.
(i) Rationalize the denominators of the following: \(
\frac{1}{\sqrt{7}} \)
Answer
Rationalizing the denominator means that we have to remove the
irrational component from the denominator of the fraction.\( \frac{1}{\sqrt{7}} \)
To remove the \( \sqrt{7} \) from the denominator, multiply and divide the fraction with \( \sqrt{7} \)
\(\frac{1}{\sqrt{7}}=\frac{1}{\sqrt{7}} \times \frac{\sqrt{7}}{\sqrt{7}}=\frac{\sqrt{7}}{7}\)
(ii) Rationalize the denominators of the following: \(
\frac{1}{\sqrt{7}-\sqrt{6}} \)
Answer
Rationalizing the denominator means that we have to remove the
irrational component from the denominator of the fraction.\( \frac{1}{\sqrt{7}-\sqrt{6}}=\frac{1}{\sqrt{7}-\sqrt{6}} \times \frac{\sqrt{7}+\sqrt{6}}{\sqrt{7}+\sqrt{6}} \)
We multiplied and divided the equation by \( \sqrt{7}+\sqrt{6} \) so that the denominator forms the formula of
\((a+b)(a-b)=a^{2}-b^{2}\)
\(\frac{1}{\sqrt{7}-\sqrt{6}}=\frac{\sqrt{7}+\sqrt{6}}{(\sqrt{7})^{2}-(\sqrt{6})^{2}}=\frac{\sqrt{7}+\sqrt{6}}{7-6}\)
\(\frac{1}{\sqrt{7}-\sqrt{6}}=\sqrt{7}+\sqrt{6}\)
(iii) Rationalize the denominators of the following: \(
\frac{1}{\sqrt{5}+\sqrt{2}} \)
Answer
Rationalizing the denominator means that we have to remove the
irrational component from the denominator of the fraction.\( \frac{1}{\sqrt{5}+\sqrt{2}}\)
\(= \frac{1(\sqrt{5}-\sqrt{2})}{(\sqrt{5}+\sqrt{2})(\sqrt{5}-\sqrt{2})}\)
\(= \frac{\sqrt{5}-\sqrt{2}}{5-2}\)
\(= \frac{\sqrt{5}-\sqrt{2}}{3}\)
(iv) Rationalize the denominators of the following: \(
\frac{1}{\sqrt{7}-2} \)
Answer
Rationalizing the denominator means that we have to remove the
irrational component from the denominator of the fraction. \( \frac{1}{\sqrt{7-2}}\)
\(=\frac{(\sqrt{7}+2)}{\sqrt{7} \times \sqrt{7}-2 \times 2}\)
\(=\frac{\sqrt{7}+2}{7-4}\)
\(=\frac{\sqrt{7}+2}{3}\)

